| Похожие рефераты | Скачать .docx |
Реферат: Линейные уравнения парной и множественной регрессии
НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"ВОЛГОГРАДСКИЙ ИНСТИТУТ БИЗНЕСА"
Кафедра
Математики и естественных наук
Домашняя контрольная работа
Дисциплина
Эконометрика
Тема: Линейные уравнения парной регрессии
Студента (ки)
Иванова Ивана Ивановича
Волгоград 2010
Задача№ 1
По данным приведенным в таблице:
1) построить линейное уравнение парной регрессии y на x;
2) рассчитать линейный коэффициент парной корреляции и оценить тесноту связи;
3) оценить статистическую значимость параметров регрессии и корреляции, используя F-статистику, t-статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей;
4) вычислить прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня.
5) оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал;
6) полученные результаты изобразить графически и привести экономическое обоснование.
Таблица №1
По территориям Центрального района известны данные за 1995 г.
| Район |
Средний размер назначенных ежемесячных пенсий, тыс.руб., y |
Прожиточный минимум в среднем на одного пенсионера в месяц, тыс.руб., х |
| Брянская обл. |
240 |
178 |
| Владимирская обл. |
226 |
202 |
| Ивановская обл. |
221 |
197 |
| Калужская обл. |
226 |
201 |
| Костромская обл. |
220 |
189 |
| Московская обл. |
237 |
215 |
| Орловская обл. |
232 |
166 |
| Рязанская обл. |
215 |
199 |
| Смоленская обл. |
220 |
180 |
| Тульская обл. |
231 |
186 |
| Ярославская обл. |
229 |
250 |
| xi |
178 |
202 |
197 |
201 |
189 |
215 |
166 |
199 |
180 |
186 |
250 |
| yi |
240 |
226 |
221 |
226 |
220 |
237 |
232 |
215 |
220 |
231 |
229 |
| Х |
Y |
| 178 |
240 |
| 202 |
226 |
| 197 |
221 |
| 201 |
226 |
| 189 |
220 |
| 215 |
237 |
| 166 |
232 |
| 199 |
215 |
| 180 |
220 |
| 186 |
231 |
| 250 |
229 |
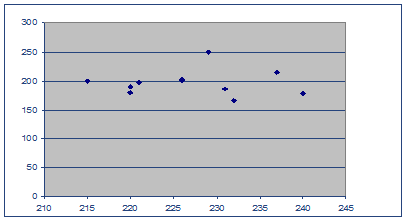
Вывод 1.
Анализ корреляционного поля данных показывает, что между признаками ![]() и
и ![]() в выборочной совокупности существует прямая и достаточно тесная связь. Предполагается, что объясняемая переменная
в выборочной совокупности существует прямая и достаточно тесная связь. Предполагается, что объясняемая переменная ![]() линейно зависит от фактора
линейно зависит от фактора ![]() , поэтому уравнение регрессии будем искать в виде
, поэтому уравнение регрессии будем искать в виде
![]() ,
,
Таблица № 4 Параметры (коэффициенты) уравнения регрессии
| Коэффициенты |
|
| Y-пересечение |
227,7117993 |
| Переменная X 1 |
-0,003619876 |
На основании этих данных запишем уравнение регрессии: ![]() .
.
Коэффициент ![]() называется выборочным коэффициентом регрессии
называется выборочным коэффициентом регрессии ![]() Коэффициент регрессии
Коэффициент регрессии ![]() показывает, на сколько единиц в среднем изменяется переменная
показывает, на сколько единиц в среднем изменяется переменная ![]() при увеличении переменной
при увеличении переменной ![]() на одну единицу.
на одну единицу.
Таблица №5. Корреляционная матрица
| Столбец 1 |
Столбец 2 |
|
| Столбец 1 |
1 |
|
| Столбец 2 |
-0,010473453 |
1 |
Для оценки качества уравнения регрессии в целом необходимо проверить статистическую значимость индекса детерминации: проверяется нулевая гипотеза ![]() , используется
, используется ![]() .
.
Таблица №6
| Регрессионная статистика |
||
| R-квадрат |
0,000109693 |
|
![]() .
.
Т.к. Значение детерминации R-квадрат имеет малое значение, которое менее 1%, то дальнейшее решение не имеет смысла, т.к. вероятность того что прогноз будет верным меньше 1%.
Задача №2
Используя данные, приведенные в таблице: построить линейное уравнение множественной регрессии;
1) оценить значимость параметров данного уравнения и построить доверительные интервалы для каждого из параметров, оценить значимость уравнения в целом, пояснить экономический смысл полученных результатов;
2) рассчитать линейные коэффициенты частной корреляции и коэффициент множественной детерминации, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними;
3) вычислить прогнозное значение y при уменьшении вектора x на 6 % от максимального уровня, оценить ошибку прогноза и построить доверительный интервал прогноза;
Таблица №5
| номер наблюдения, i |
Накопления семьи, Y (y.e.) |
Доход семьи, X1 ( y. e.) |
Расходы на питание, X 2 ( y. e.) |
| 1 |
2 |
20 |
5 |
| 2 |
6 |
27 |
6 |
| 3 |
7 |
26 |
7 |
| 4 |
5 |
19 |
5 |
| 5 |
4 |
15 |
5 |
| 6 |
2 |
15 |
5 |
| 7 |
7 |
28 |
10 |
| 8 |
6 |
24 |
7 |
| 9 |
4 |
14 |
6 |
| 10 |
5 |
21 |
7 |
| 11 |
5 |
20 |
10 |
| 12 |
3 |
18 |
6 |
Таблица №6 Параметры (коэффициенты) уравнения регрессии
| Коэффициенты |
|
| Y-пересечение |
-1,767785782 |
| x1 |
0,232792618 |
| x2 |
0,24953991 |
Множественная регрессия широко используется в решении проблем спроса, доходности акций, изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия - один из наиболее распространенных методов в эконометрике . Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
На основании этих данных запишем уравнение регрессии:
![]() .
.
Таблица №7 Регрессионная статистика
| R-квадрат |
0,663668925 |
| Нормированный R-квадрат |
0,588928686 |
! Параметр R-квадрат, представляет собой квадрат коэффициента корреляции rxy 2 и называется коэффициентом детерминации . Величина данного коэффициента характеризует долю дисперсии зависимой переменной y, объясненную регрессией (объясняющей переменной x). Соответственно величина 1 - rxy 2 характеризует долю дисперсии переменной y, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных. Доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет: 0,663668, или 66,3%.
Находим, что численное значение ![]() , а скорректированный (нормированный, исправленный) коэффициент детерминации равен
, а скорректированный (нормированный, исправленный) коэффициент детерминации равен ![]()
1) Для оценки качества уравнения регрессии в целом необходимо проверить статистическую значимость индекса детерминации ![]() : проверяется нулевая гипотеза
: проверяется нулевая гипотеза ![]() , используется
, используется ![]() .
.
Наблюдаемое значение критерия ![]() и оценку его значимости находим в Таблице №8
и оценку его значимости находим в Таблице №8
Таблица №8 Дисперсионный анализ:
| F |
Значимость F |
| 8,87967358 |
0,007420813 |
! Включаемые в уравнение множественной регрессии факторы должны объяснить вариацию зависимой переменной . Если строится модель с некоторым набором факторов, то для нее рассчитывается показатель детерминации , который фиксирует долю объясненной вариации результативного признака (объясняемой переменной ) за счет рассматриваемых в регрессии факторов. А оценка влияния других, неучтенных в модели факторов, оценивается вычитанием из единицы коэффициента детерминации , что и приводит к соответствующей остаточной дисперсии .
Таким образом, при дополнительном включении в регрессию еще одного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит и данные показатели практически недостаточно значимо отличаются друг от друга, то включаемый в анализ дополнительный фактор не улучшает модель и практически является лишним фактором.
Если модель насыщается такими лишними факторами, то не только не снижается величина остаточной дисперсии и не увеличивается показатель детерминации, но, более того, снижается статистическая значимость параметров регрессии по критерию Стьюдента вплоть до статистической незначимости.
2) Для статистической оценки значимости коэффициентов регрессии (![]() ) используем
) используем ![]() статистику Стьюдента.
статистику Стьюдента.
Проверяется нулевая гипотеза ![]() .
.
Для проверки нулевой гипотезы необходимо знать величину наблюдаемых значений критерия ![]() . Их значения и оценки их статистической значимости найдем в Таблице №9
. Их значения и оценки их статистической значимости найдем в Таблице №9
Таблица №9
| t-статистика |
P-Значение |
| -1,127971079 |
0,28850322 |
| 2,838964459 |
0,01943598 |
| 1,130728736 |
0,28740002 |
В этой же таблице находим границы доверительных интервалов для каждого из параметров:
| Нижние 95% |
Верхние 95% |
| -5,313097658 |
1,777526094 |
| 0,047297697 |
0,418287538 |
| -0,249694323 |
0,748774142 |
3. Значения парных коэффициентов корреляции найдем из соответствующей матрицы.
Таблица №10 Корреляционная матрица
| y |
x1 |
x2 |
|
| y |
1 |
||
| x1 |
0,784786247 |
1 |
|
| x2 |
0,60206001 |
0,531178469 |
1 |
По величине парных коэффициентов корреляции может обнаруживаться лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью , т.е. имеет место совокупное воздействие факторов друг на друга.
Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).
Частные коэффициенты корреляции найдем по формулам
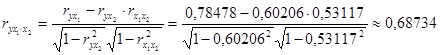 ,
,
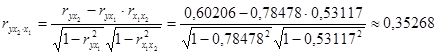 ,
,
их значения показывают, что при отсутствии влияния других факторов, связь с рассматриваемым фактором усиливается т.е. мультиколлинеарность между ними существует.
4. Рассчитаем прогнозное значение результата, если прогнозные значения факторов составляют 110% их максимального значения. Найдем прогнозные значения факторов и подставим их в полученное уравнение регрессии.
По условию прогнозные значения составляют 110% их максимального значения.
Таблица №11
| maxX1 |
maxX2 |
| 28 |
10 |
Далее вычисляем прогнозные значения факторов: ![]() . Затем, подставив эти значения в уравнение регрессии, получим прогнозное (предсказанное) значение фактора
. Затем, подставив эти значения в уравнение регрессии, получим прогнозное (предсказанное) значение фактора ![]() . Доверительный интервал прогноза оценивается формулой:
. Доверительный интервал прогноза оценивается формулой: ![]() , где
, где ![]() - ошибка прогноза,
- ошибка прогноза,![]() стандартная ошибка регрессии.
стандартная ошибка регрессии.
Таблица №12
| Стандартная ошибка |
1,104878833 |
![]() ;
;
![]() - коэффициент Стьюдента, который в данном случае имеет смысл кратности случайной (стандартной) ошибки прогноза
- коэффициент Стьюдента, который в данном случае имеет смысл кратности случайной (стандартной) ошибки прогноза ![]() ;
;
![]() - число, которое получим в результате операций над матрицами:
- число, которое получим в результате операций над матрицами:
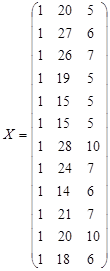 -
-
матрица значений факторных переменных ![]() ,
,
![]() транспонированная матрица
транспонированная матрица ![]() ;
;
![]() - произведение матриц
- произведение матриц ![]() ;
;
![]() - матрица, обратная к матрице
- матрица, обратная к матрице ![]() ;
;
![]() - матрица прогнозных значений факторов;
- матрица прогнозных значений факторов;
![]() - транспонированная матрица прогнозов.
- транспонированная матрица прогнозов.
Фактор ![]() представляет собой фиктивную переменную, которую необходимо ввести в уравнение регрессии для того, чтобы преобразовать его в "приведенную" форму вида
представляет собой фиктивную переменную, которую необходимо ввести в уравнение регрессии для того, чтобы преобразовать его в "приведенную" форму вида ![]() .
.
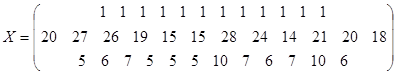
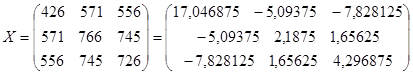
Максимальную ошибку прогноза ![]() =11,07714043: 1) нижняя граница прогноза
=11,07714043: 1) нижняя граница прогноза ![]() =44,92285957, 2) верхнюю границу прогноза
=44,92285957, 2) верхнюю границу прогноза ![]() =67,07714043. Интервал прогнозных значений результативного признака
=67,07714043. Интервал прогнозных значений результативного признака
![]() =>
=>![]()
Задача № 3
Используя данные, представленные в таблице проверить наличие гетероскедастичности, применяя тест Голдфельда-Квандта.
Таблица№13. Данные
| Страна |
Индекс человеческого развития, У |
Расходы на конечное потребление в текущих ценах, % к ВВП, Х |
| 0,904 |
75,5 |
|
| Австралия |
0,922 |
78,5 |
| Англия |
0,918 |
84,4 |
| Белоруссия |
0,763 |
78,4 |
| Бельгия |
0,923 |
77,7 |
| Германия |
0,906 |
75,9 |
| Дания |
0,905 |
76,0 |
| Индия |
0,545 |
67,5 |
| Испания |
0,894 |
78,2 |
| Италия |
0,900 |
78,1 |
| Канада |
0,932 |
78,6 |
| Казахстан |
0,740 |
84,0 |
| Китай |
0,701 |
59,2 |
| Латвия |
0,744 |
90,2 |
| Нидерланды |
0,921 |
72,8 |
| Норвегия |
0,927 |
67,7 |
| Польша |
0,802 |
82,6 |
| Россия |
0,747 |
74,4 |
| США |
0,927 |
83,3 |
| Украина |
0,721 |
83,7 |
| Финляндия |
0,913 |
73,8 |
| Франция |
0,918 |
79,2 |
| Чехия |
0,833 |
71,5 |
| Швейцария |
0,914 |
75,3 |
| Швеция |
0,923 |
79,0 |
1) Найдем параметры линейного уравнения множественной регрессии и значения остатков.
Определим остаточные суммы квадратов ![]() и
и ![]() , то есть суммы квадратов остатков регрессии по "урезанным выборкам".
, то есть суммы квадратов остатков регрессии по "урезанным выборкам".
Таблица№14
| № |
Y |
X |
Yp |
ei |
(ei) ^2 |
|
| 1 |
0,932 |
78,6 |
77,90431365 |
0,695686352 |
0,483979501 |
|
| 2 |
0,927 |
67,7 |
77,85057558 |
-10,15057558 |
103,0341846 |
|
| 3 |
0,927 |
83,3 |
77,85057558 |
5,44942442 |
29,69622651 |
|
| 4 |
0,923 |
77,7 |
77,80758513 |
-0,107585125 |
0,011574559 |
|
| 5 |
0,923 |
79,0 |
77,80758513 |
1, 192414875 |
1,421853234 |
|
| 6 |
0,922 |
78,5 |
77,79683751 |
0,703162488 |
0,494437485 |
|
| 7 |
0,921 |
72,8 |
77,7860899 |
-4,986089898 |
24,86109247 |
|
| 8 |
0,918 |
84,4 |
77,75384706 |
6,646152943 |
44,17134894 |
S1 |
| 9 |
0,918 |
79,2 |
77,75384706 |
1,446152943 |
2,091358334 |
206,2660556 |
| 10 |
0,914 |
75,3 |
77,7108566 |
-2,410856603 |
5,812229559 |
|
| 11 |
0,913 |
73,8 |
77,70010899 |
-3,900108989 |
15,21085013 |
|
| 12 |
0,906 |
75,9 |
77,62487569 |
-1,724875694 |
2,975196159 |
|
| 13 |
0,905 |
76,0 |
77,61412808 |
-1,61412808 |
2,60540946 |
|
| 14 |
0,904 |
75,5 |
77,60338047 |
-2,103380467 |
4,424209388 |
|
| 15 |
0,900 |
78,1 |
77,56039001 |
0,539609988 |
0,291178939 |
|
| 16 |
0,894 |
78,2 |
77,49590433 |
0,704095669 |
0,495750712 |
|
| 17 |
0,833 |
71,5 |
76,8402999 |
-5,3402999 |
28,51880303 |
|
| 18 |
0,802 |
82,6 |
76,50712388 |
6,092876121 |
37,12313943 |
|
| 19 |
0,763 |
78,4 |
76,08796695 |
2,312033052 |
5,345496834 |
|
| 20 |
0,747 |
74,4 |
75,91600513 |
-1,51600513 |
2,298271555 |
|
| 21 |
0,744 |
90,2 |
75,88376229 |
14,31623771 |
204,9546622 |
|
| 22 |
0,740 |
84,0 |
75,84077183 |
8,159228165 |
66,57300425 |
|
| 23 |
0,721 |
83,7 |
75,63656718 |
8,063432824 |
65,0189489 |
|
| 24 |
0,701 |
59,2 |
75,4216149 |
-16,2216149 |
263,1407901 |
S2 |
| 25 |
0,545 |
67,5 |
73,74498718 |
-6,244987181 |
38,99986489 |
743,7878055 |
1) Находим наблюдаемое значение критерия ![]() . По условию задачи
. По условию задачи ![]() . Из таблицы значений
. Из таблицы значений ![]() Фишера находим, что
Фишера находим, что ![]()
Вывод: отвергаем нулевую гипотезу ![]() на принятом уровне значимости
на принятом уровне значимости ![]() , т.к. наблюдаемое значение критерия больше табличного.
, т.к. наблюдаемое значение критерия больше табличного.
Следовательно, предположение об однородности дисперсий ошибок, при условии, что выполнены стандартные предположения о модели наблюдений, включая предположение о нормальности ошибок, неверно. Наблюдается гетероскедастичность, что приводит к ошибочным статистическим выводам при использовании МНК. Следовательно, полученные оценки не являются состоятельными.
Задача № 4
По данным таблицы построить уравнение регрессии, выявить наличие автокорреляции остатков, используя критерий Дарбина - Уотсона, и проанализировать пригодность полученного уравнения для построения прогнозов.
Таблица №15
| Год |
Выпуск продукции в США в среднем за 1 час, % к уровню 1982 г., Х |
Среднечасовая заработная плата в экономике США, в сопоставимых ценах 1982 г., Y |
| 1960 |
65,6 |
6,79 |
| 1961 |
68,1 |
6,88 |
| 1962 |
73,3 |
7,07 |
| 1963 |
76,5 |
7,17 |
| 1964 |
78,6 |
7,33 |
| 1965 |
81,0 |
7,52 |
| 1966 |
83,0 |
7,62 |
| 1967 |
85,4 |
7,72 |
| 1968 |
85,9 |
7,89 |
| 1969 |
85,9 |
7,98 |
| 1970 |
87,0 |
8,03 |
| 1971 |
90,2 |
8,21 |
| 1972 |
92,6 |
8,53 |
| 1973 |
95,0 |
8,55 |
| 1974 |
93,3 |
8,28 |
| 1975 |
95,5 |
8,12 |
Найдем параметры линейного уравнения множественной регрессии и значения остатков.
Дополним таблицу данных столбцами "![]() ", "Квадрат разности остатков
", "Квадрат разности остатков ![]() " и "Квадрат остатка
" и "Квадрат остатка ![]() " и заполним их.
" и заполним их.
Таблица №16
| Y |
X |
Yi |
et |
et-1 |
(et-et-1) ^2 |
et^2 |
| 6,79 |
65,6 |
6,667235239 |
0,122765 |
0,015071 |
||
| 6,88 |
68,1 |
6,815288112 |
0,064712 |
0,122765 |
0,003370136 |
0,004188 |
| 7,07 |
73,3 |
7,123238088 |
-0,05324 |
0,064712 |
0,013912197 |
0,002834 |
| 7,17 |
76,5 |
7,312745766 |
-0,14275 |
-0,05324 |
0,008011624 |
0,020376 |
| 7,33 |
78,6 |
7,437110179 |
-0,10711 |
-0,14275 |
0,001269895 |
0,011473 |
| 7,52 |
81,0 |
7,579240937 |
-0,05924 |
-0,10711 |
0,002291464 |
0,003509 |
| 7,62 |
83,0 |
7,697683236 |
-0,07768 |
-0,05924 |
0,000340118 |
0,006035 |
| 7,72 |
85,4 |
7,839813994 |
-0,11981 |
-0,07768 |
0,001775001 |
0,014355 |
| 7,89 |
85,9 |
7,869424568 |
0,020575 |
-0,11981 |
0,019709191 |
0,000423 |
| 7,98 |
85,9 |
7,869424568 |
0,110575 |
0,020575 |
0,008100000 |
0,012227 |
| 8,03 |
87,0 |
7,934567833 |
0,095432 |
0,110575 |
0,000229318 |
0,009107 |
| 8,21 |
90,2 |
8,12407551 |
0,085924 |
0,095432 |
0,000090396 |
0,007383 |
| 8,53 |
92,6 |
8,266206268 |
0,263794 |
0,085924 |
0,031637467 |
0,069587 |
| 8,55 |
95,0 |
8,408337026 |
0,141663 |
0,263794 |
0,014915922 |
0,020068 |
| 8,28 |
93,3 |
8,307661073 |
-0,02766 |
0,141663 |
0,028670633 |
0,000765 |
| 8,12 |
95,5 |
8,437947601 |
-0,31795 |
-0,02766 |
0,084266268 |
0,101091 |
| Суммы |
0,218589631 |
0,298494 |
По формуле 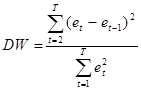 вычислим значение статистики
вычислим значение статистики ![]() :
:
Так как ![]() , то значение статистики
, то значение статистики
равно ![]() .
.
По таблице критических точек Дарбина Уотсона определим значения критерия Дарбина-Уотсона ![]() (нижнее) и
(нижнее) и ![]() (верхнее) для заданного числа наблюдений
(верхнее) для заданного числа наблюдений ![]() , числа независимых переменных модели
, числа независимых переменных модели ![]() и уровня значимости
и уровня значимости ![]() . Итак, находим, что
. Итак, находим, что ![]() ,
, ![]() .
.
По этим значениям числовой промежуток ![]() разбиваем на пять отрезков:
разбиваем на пять отрезков:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
На основании выполненных расчетов находим, что наблюдаемое значение статистики ![]() принадлежит первому интервалу.
принадлежит первому интервалу.
Вывод: существует отрицательная автокорреляция, то есть гипотеза ![]() отклоняется и с вероятностью
отклоняется и с вероятностью ![]() принимается гипотеза
принимается гипотеза ![]() .
.
Следовательно, полученное уравнение регрессии ![]() не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна.
не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна.
Задача № 5
В таблице приводятся данные о динамике выпуска продукции Финляндии (млн. долл.).
Таблица №17
| Год |
Выпуск продукции, yt млн.долл. |
| 1989 |
23 298 |
| 1990 |
26 570 |
| 1991 |
23 080 |
| 1992 |
29 800 |
| 1993 |
28 440 |
| 1994 |
29 658 |
| 1995 |
39 573 |
| 1996 |
38 435 |
| 1997 |
39 002 |
| 1998 |
39 020 |
| 1999 |
40 012 |
| 2000 |
41 005 |
| 2001 |
39 080 |
| 2002 |
42 680 |
Задание:
1. Постройте график временного ряда.
2. Сделайте вывод о присутствии или отсутствии тренда при доверительной вероятности 0,95.
3. Найдите среднее значение, среднеквадратическое отклонение и коэффициенты автокорреляции (для лагов ![]() ) заданного ВР.
) заданного ВР.
4. Проведите сглаживание данного ВР методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания ![]() ;
;
5. Найдите уравнение тренда ВР ![]() , предполагая, что он линейный, и проверьте его значимость на уровне
, предполагая, что он линейный, и проверьте его значимость на уровне ![]() .
.
6. Дайте точечный и интервальный (с надежностью 0,95) прогнозы индивидуального значения выпуска продукции на 2003 год.
Таблица №18
| Год |
t |
Выпуск продукции, yt млн.долл. |
| 1989 |
1 |
23 298 |
| 1990 |
2 |
26 570 |
| 1991 |
3 |
23 080 |
| 1992 |
4 |
29 800 |
| 1993 |
5 |
28 440 |
| 1994 |
6 |
29 658 |
| 1995 |
7 |
39 573 |
| 1996 |
8 |
38 435 |
| 1997 |
9 |
39 002 |
| 1998 |
10 |
39 020 |
| 1999 |
11 |
40 012 |
| 2000 |
12 |
41 005 |
| 2001 |
13 |
39 080 |
| 2002 |
14 |
42 680 |
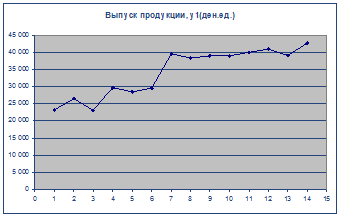
2. Для обнаружения тенденции в данном ВР воспользуемся критерием "восходящих и нисходящих" серий.
Критерий "восходящих и нисходящих" серий
1) Для исследуемого ВР определяется последовательность знаков, исходя из условий: (+), если ![]() , (-), если
, (-), если ![]() .
.
При этом, если последующее наблюдение равно предыдущему, то учитывается только одно наблюдение.
2) Подсчитывается число серий ![]() . Под серией понимается последовательность подряд расположенных плюсов или минусов, причем один плюс или один минус считается серией.
. Под серией понимается последовательность подряд расположенных плюсов или минусов, причем один плюс или один минус считается серией.
3) Определяется протяженность самой длинной серии ![]() .
.
4) Значение ![]() находят из следующей таблицы:
находят из следующей таблицы:
Таблица №25
| Длина ряда, |
|
|
|
| Значение |
5 |
6 |
7 |
5) Если нарушается хотя бы одно из следующих неравенств, то гипотеза об отсутствии тренда отвергается с доверительной вероятностью 0,95
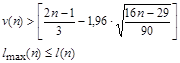
Определим последовательность знаков:
Таблица №19
| t |
Выпуск продукции, yt млн.долл. |
|
| 1 |
23 298 |
|
| 2 |
26 570 |
+ |
| 3 |
23 080 |
- |
| 4 |
29 800 |
+ |
| 5 |
28 440 |
- |
| 6 |
29 658 |
+ |
| 7 |
39 573 |
+ |
| 8 |
38 435 |
- |
| 9 |
39 002 |
+ |
| 10 |
39 020 |
+ |
| 11 |
40 012 |
+ |
| 12 |
41 005 |
+ |
| 13 |
39 080 |
- |
| 14 |
42 680 |
+ |
Определим число серий ![]() :
: ![]() . Определим протяженность самой длинной серии
. Определим протяженность самой длинной серии ![]() :
: ![]() .
. ![]() , так как
, так как ![]() . Проверим выполнение неравенств:
. Проверим выполнение неравенств:
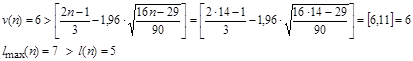
Вывод: второе неравенство не выполняются, следовательно, тренд (тенденция) в динамике выпуска продукции имеется на уровне значимости 0,05. Среднее значение ![]() . Среднее значение
. Среднее значение ![]() . Вычислим коэффициенты автокорреляции первого и второго порядков, то есть для лагов
. Вычислим коэффициенты автокорреляции первого и второго порядков, то есть для лагов ![]() . Подготовим данные для вычисления коэффициентов автокорреляции первого и второго порядков. Дополним таблицу данных двумя столбцами
. Подготовим данные для вычисления коэффициентов автокорреляции первого и второго порядков. Дополним таблицу данных двумя столбцами ![]() .
.
Таблица №20
| t |
Yt |
Yt-1 |
Yt-2 |
| 1 |
23 298 |
||
| 2 |
26 570 |
23 298 |
|
| 3 |
23 080 |
26 570 |
23 298 |
| 4 |
29 800 |
23 080 |
26 570 |
| 5 |
28 440 |
29 800 |
23 080 |
| 6 |
29 658 |
28 440 |
29 800 |
| 7 |
39 573 |
29 658 |
28 440 |
| 8 |
38 435 |
39 573 |
29 658 |
| 9 |
39 002 |
38 435 |
39 573 |
| 10 |
39 020 |
39 002 |
38 435 |
| 11 |
40 012 |
39 020 |
39 002 |
| 12 |
41 005 |
40 012 |
39 020 |
| 13 |
39 080 |
41 005 |
40 012 |
| 14 |
42 680 |
39 080 |
41 005 |
![]() .
.
![]() .
.
Вывод:
1) высокое значение коэффициента автокорреляции первого порядка ![]() свидетельствует об очень тесной зависимости между выпуском продукции текущего и непосредственно предшествующего годов, и, следовательно, о наличии в исследуемом временном ряде сильной линейной тенденции;
свидетельствует об очень тесной зависимости между выпуском продукции текущего и непосредственно предшествующего годов, и, следовательно, о наличии в исследуемом временном ряде сильной линейной тенденции;
2) исследуемый ряд содержит только тенденцию, так как наиболее высоким оказался коэффициент автокорреляции первого порядка (0,85>0,83).
Скользящие средние найдем по формуле: ![]() , здесь
, здесь ![]() . При
. При ![]()
Вычисляем:
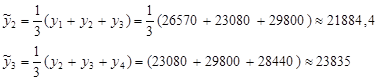
и так далее.
Результаты вычислений занесем в таблицу и построим графики исходного![]() и сглаженного
и сглаженного ![]() рядов в одной координатной плоскости.
рядов в одной координатной плоскости.
Таблица №21
| t |
yi |
yt |
| 1 |
23 298 |
|
| 2 |
26 570 |
24 315,76 |
| 3 |
23 080 |
26 483,07 |
| 4 |
29 800 |
27 106,40 |
| 5 |
28 440 |
29 299,04 |
| 6 |
29 658 |
32 556,67 |
| 7 |
39 573 |
35 888,31 |
| 8 |
38 435 |
39 002,94 |
| 9 |
39 002 |
38 818,61 |
| 10 |
39 020 |
39 344,27 |
| 11 |
40 012 |
40 011,93 |
| 12 |
41 005 |
40 031,93 |
| 13 |
39 080 |
40 921,26 |
| 14 |
42 680 |
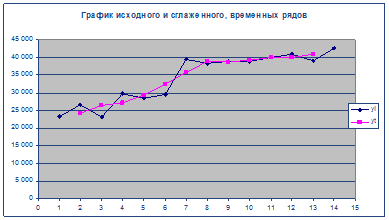
Таблица № Параметры (коэффициенты) уравнения тренда.
Таблица №22
| Коэффициенты |
|
| Y-пересечение |
22686,54945 |
| t |
1543,250549 |
Анализ данных таблицы Дисперсионного анализа показывает, что получено статистически значимое уравнение, так как наблюдаемое значение ![]() , равное 52,785, превышает его табличное значение
, равное 52,785, превышает его табличное значение ![]() ,
, ![]() . Вывод: Таким образом, параметры уравнения тренда статистически значимы на уровне
. Вывод: Таким образом, параметры уравнения тренда статистически значимы на уровне ![]() : уравнение тренда можно использовать для прогноза.
: уравнение тренда можно использовать для прогноза.
Сделаем точечный и интервальный (с надежностью 0,95) прогнозы среднего и индивидуального значений прогнозов на 2003 год.
Определим точечный прогноз
![]()
![]()
Вычислим интервальный прогноз:
Так как тренд является прямой, то доверительный интервал можно представить в виде: ![]()
![]() .
.
Здесь стандартная ошибка предсказания по линии тренда ![]() вычисляется по формуле:
вычисляется по формуле:
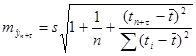 ,
,
здесь величина ![]() является стандартной ошибкой регрессии, и ее значение находится в таблице Регрессионная статистика
является стандартной ошибкой регрессии, и ее значение находится в таблице Регрессионная статистика
Таблица №23
| Стандартная ошибка |
1637,180026 |
![]() кратность ошибки (надежность) находят по таблице значений критерия Стьюдента;
кратность ошибки (надежность) находят по таблице значений критерия Стьюдента; ![]() уровень значимости;
уровень значимости; ![]() число степеней свободы.
число степеней свободы.
Итак, по условию задачи имеем: ![]()
Для вычисления стандартной ошибки предсказания по линии тренда ![]() необходимо вычислить
необходимо вычислить ![]() и сумму
и сумму ![]() .
.
Таблица № 24
| t |
yt |
(t1-tcr) ^2 |
| 1 |
23 298 |
42,25 |
| 2 |
26 570 |
30,25 |
| 3 |
23 080 |
20,25 |
| 4 |
29 800 |
12,25 |
| 5 |
28 440 |
6,25 |
| 6 |
29 658 |
2,25 |
| 7 |
39 573 |
0,25 |
| 8 |
38 435 |
0,25 |
| 9 |
39 002 |
2,25 |
| 10 |
39 020 |
6,25 |
| 11 |
40 012 |
12,25 |
| 12 |
41 005 |
20,25 |
| 13 |
39 080 |
30,25 |
| 14 |
42 680 |
42,25 |
| 7,5 |
Сумма |
227,5 |
Вычисляем 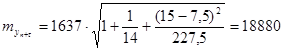 (млн. долл.)
(млн. долл.)
По таблице значений критерия Стьюдента найдем ![]()
Максимальная ошибка прогноза будет равна:
![]() (млн. долл.).
(млн. долл.).
Нижняя граница прогноза имеет значение ![]() (млн. долл.)
(млн. долл.)
Верхняя граница прогноза имеет значение ![]() (млн. долл.)
(млн. долл.)
Вывод:
1) значение выпуска продукции Финляндии в 2003 составит 20111,2 млн. долл.
2) с надежностью 0,95 данное значение будет находиться в интервале ![]()
Похожие рефераты:
Методы прогноза лавинной опасности
Экономическое планирование методами математической статистики
Демографическая ситуация в Республике Бурятия
Социальное прогнозирование в сфере демографических процессов
Расчет показателей эконометрики
Линейный множественный регрессивный анализ
Планирование и прогнозирование доходов бюджетов органов местного самоуправления
Построение математических моделей
Составление и решение уравнений линейной регрессии