| Скачать .zip |
Реферат: Статистическая обработка экспериментальных данных
Аннотация
Темой курсовой работы является "Статистическая обработка экспериментальных данных". Целью курсовой работы является закрепление изученного материала по дисциплине "Метрология, стандартизация и сертификация" и приобретение практических навыков обработки экспериментальных данных различных видов измерений.
В курсовой работе приведены:
– в разделе "Однократные измерения": порядок выполнения однократного измерения, внесены необходимые поправки и определен предел, в котором находится значение измеряемой величины;
– в разделе "Многократные измерения": результаты измерений, порядок выполнения многократного измерения, исключены ошибки из результатов измерений и определен результат измерений;
– в разделе "Обработка результатов нескольких серий измерений": серии результатов измерений, порядок их обработки и результат измерения;
– в разделе "Косвенные измерения": функциональная зависимость между искомой величиной Z и измеряемыми величинами X и Y, определены и внесены поправки и определен результат измерения;
– в разделе "Определение погрешностей результатов измерений методом математической статистики": результаты измерения, выстроены: гистограмма нормального рассеяния измерений и график реального рассеяния измерений в едином масштабе.
Курсовая работа содержит 30 листов расчетно-пояснительной записки.



СОДЕРЖАНИЕ
Курсовая работа 1
Введение 3
1. Однократное измерение 4
2. Многократное измерение 6
3. Обработка результатов нескольких серий измерений 13
4. Функциональные преобразования результатов измерений (косвенные измерения) 19
5. Определение погрешностей результатов измерений методом математической статистики 25
29
Литература 30
Введение
Измерения — один из важнейших путей познания природы человеком. Они играют огромную роль в современном обществе. Наука и промышленность не могут существовать без измерений. Практически нет ни одной сферы деятельности человека, где бы интенсивно не использовались результаты измерений, испытаний и контроля.
Диапазон измерительных величин и их количество постоянно растут и поэтому возрастает и сложность измерений. Они перестают быть одноактным действием и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента и обработки полученной информации.
Другой причиной важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, контроля или регулирования — достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.
1. Однократное измерение
Условие. При однократном измерении физической величины получено показание средства измерения X = 10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерений и условиях выполнения измерений, согласно исходным данным.
Исходные данные:
Показание средства измерения – X = 10.
Вид закона распределения – равномерный.
Значение оценки среднеквадратического отклонения – SX = 0,8.
Значение аддитивной поправки – Θa = 0,9.
Расчет. Так как в качестве априорной используется информация о законе распределения вероятности, т.е. закон распределения вероятности является равномерным, то пределы, в которых находится значение измеряемой величины, определяются через доверительный интервал:
![]() ;
; ![]() (1)
(1)
Для равномерного закона распределения вероятности результата измерения значение E (аналог доверительного интервала) можно определить из выражения:
![]() ,
(2)
,
(2)
где
![]() .
.
![]()
![]()
![]()
Внесем аддитивную поправку и уточним пределы, в которых находится значение измеряемой величины.
![]()
![]()
![]()
![]()
2. Многократное измерение
Условие.
При многократном
измерении одной
и той же физической
величины получена
серия из 24 результатов
измерений Qi;
![]() .
Определить
результат
измерения.
.
Определить
результат
измерения.
Исходные данные:
Таблица 1
| № изме-рения | Результат измерения | № изме-рения | Результат измерения | № изме-рения | Результат измерения | № изме-рения | Результат измерения |
| 1 | 482 | 7 | 483 | 13 | 483 | 19 | 483 |
| 2 | 485 | 8 | 483 | 14 | 483 | 20 | 482 |
| 3 | 486 | 9 | 481 | 15 | 483 | 21 | 481 |
| 4 | 486 | 10 | 480 | 16 | 483 | 22 | 481 |
| 5 | 483 | 11 | 492 | 17 | 484 | 23 | 483 |
| 6 | 483 | 12 | 486 | 18 | 484 | 24 | 495 |
Расчет. Порядок расчета и их содержание определяются условием:
10…15 < n< 40…50,
так как n = 24.
1. Определяем
оценки результата
измерения
![]() и среднего
квадратического
отклонения
результата
измерения
и среднего
квадратического
отклонения
результата
измерения
![]() .
.
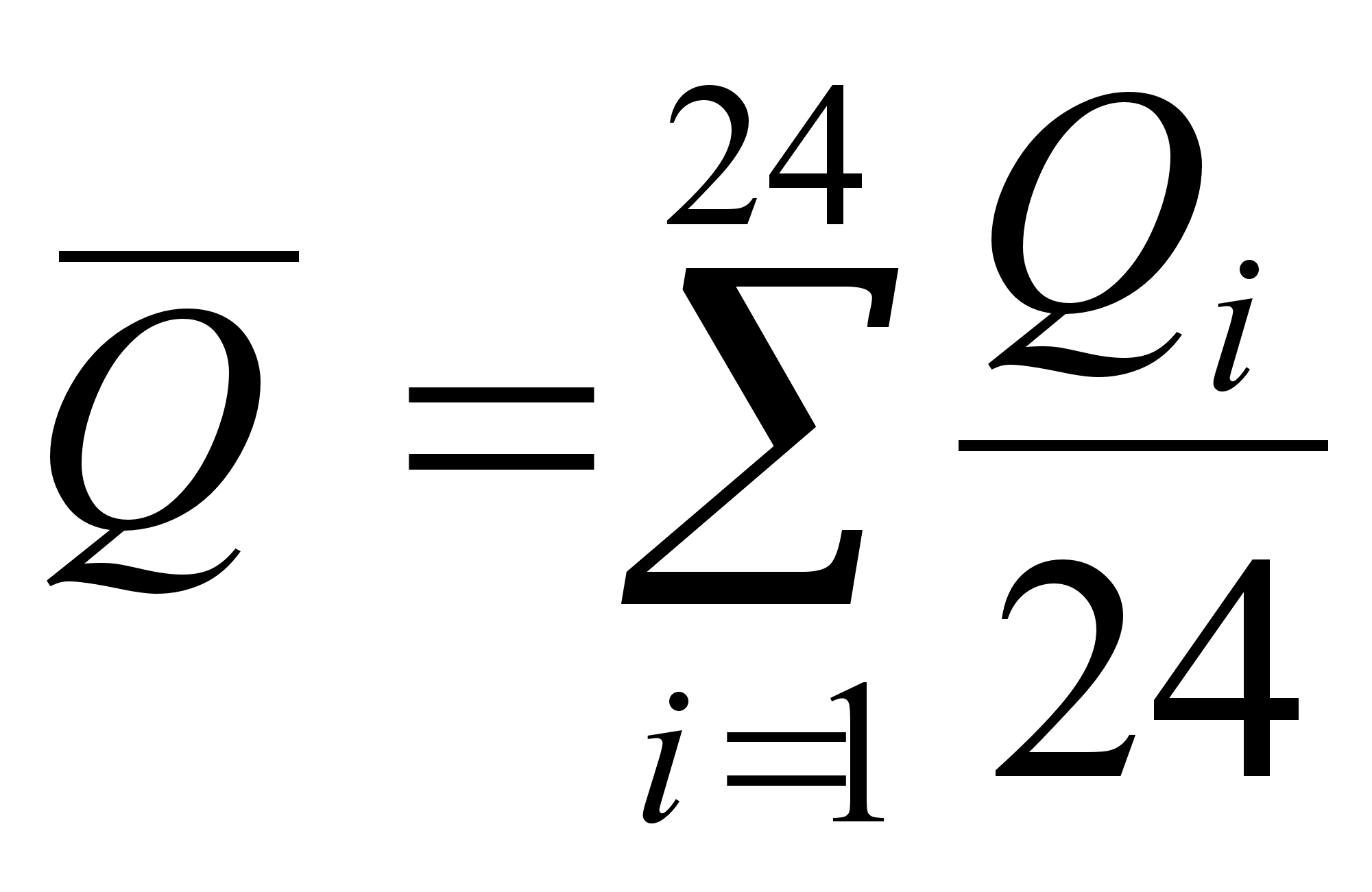
![]() (3)
(3)
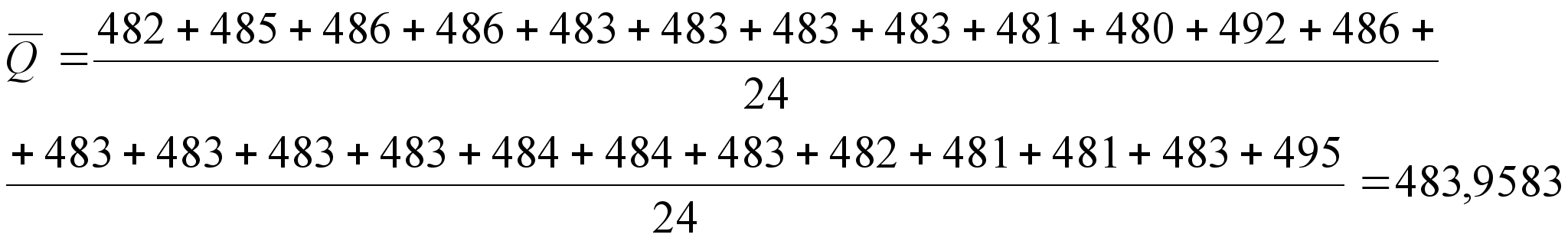
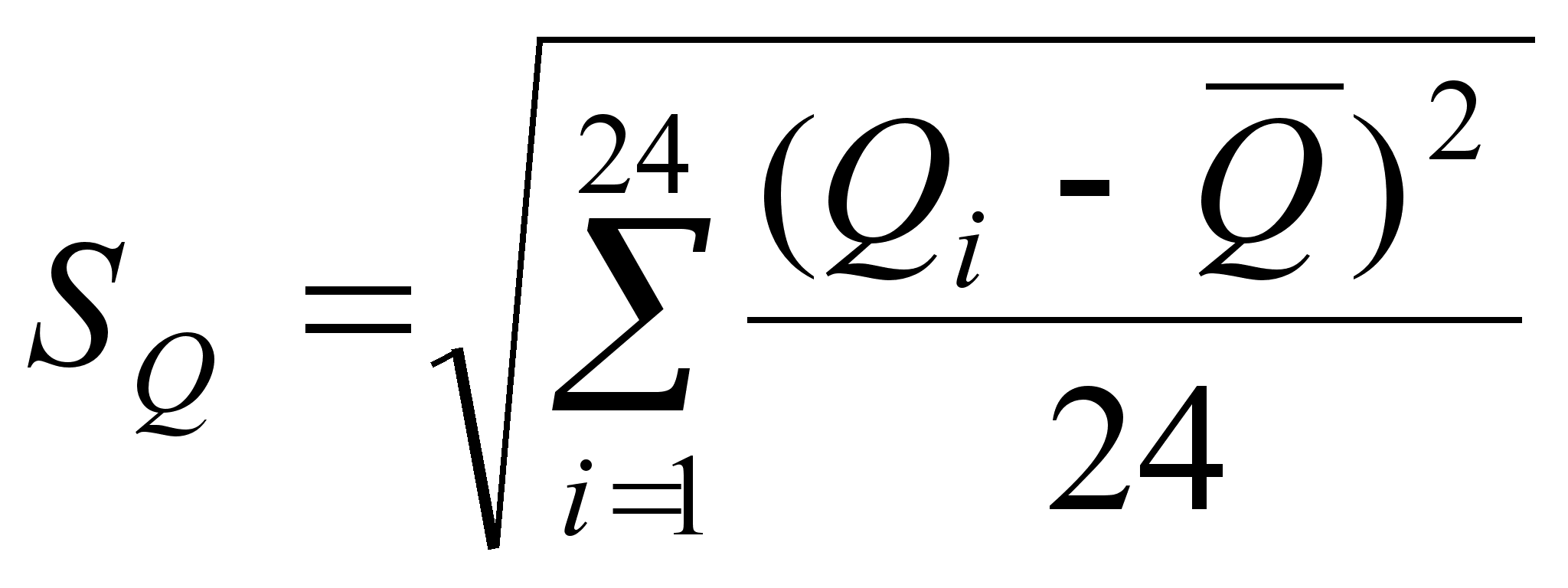 (4)
(4)
Для удобства
вычисления
среднего
квадратического
отклонения
результата
измерения
![]() составим таблицу:
составим таблицу:
Таблица 2
| № из-мерения |
Результат измере-ния (Qi) |
|
|
№ из-мерения |
Результат измере-ния (Qi) |
|
|
| 1 | 482 | -1,9583 | 3,8351 | 13 | 483 | -0,9583 | 0,9184 |
| 2 | 485 | 1,0417 | 1,0851 | 14 | 483 | -0,9583 | 0,9184 |
| 3 | 486 | 2,0417 | 4,1684 | 15 | 483 | -0,9583 | 0,9184 |
| 4 | 486 | 2,0417 | 4,1684 | 16 | 483 | -0,9583 | 0,9184 |
| 5 | 483 | -0,9583 | 0,9184 | 17 | 484 | 0,0417 | 0,0017 |
| 6 | 483 | -0,9583 | 0,9184 | 18 | 484 | 0,0417 | 0,0017 |
| 7 | 483 | -0,9583 | 0,9184 | 19 | 483 | -0,9583 | 0,9184 |
| 8 | 483 | -0,9583 | 0,9184 | 20 | 482 | -1,9583 | 3,8351 |
| 9 | 481 | -2,9583 | 8,7517 | 21 | 481 | -2,9583 | 8,7517 |
| 10 | 480 | -3,9583 | 15,6684 | 22 | 481 | -2,9583 | 8,7517 |
| 11 | 492 | 8,0417 | 64,6684 | 23 | 483 | -0,9583 | 0,9184 |
| 12 | 486 | 2,0417 | 4,1684 | 24 | 495 | 11,0417 | 121,9184 |
|
Σ |
0 |
258,9583 |
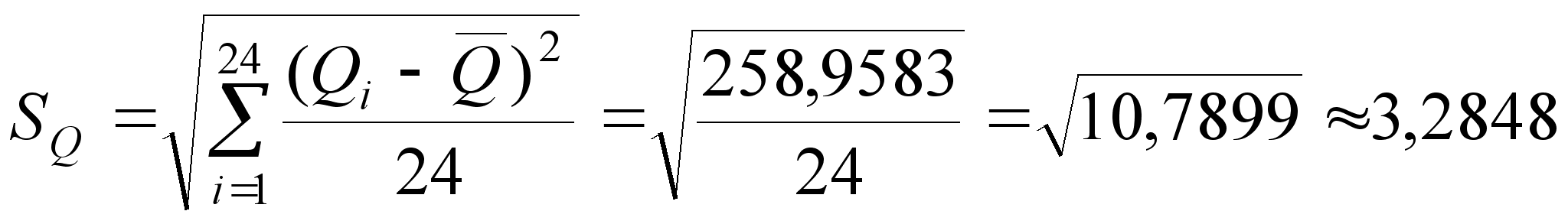
2. Необходимо обнаружить и исключить ошибки. Для этого:
– вычисляем наибольшее по абсолютному значению нормированное отклонение
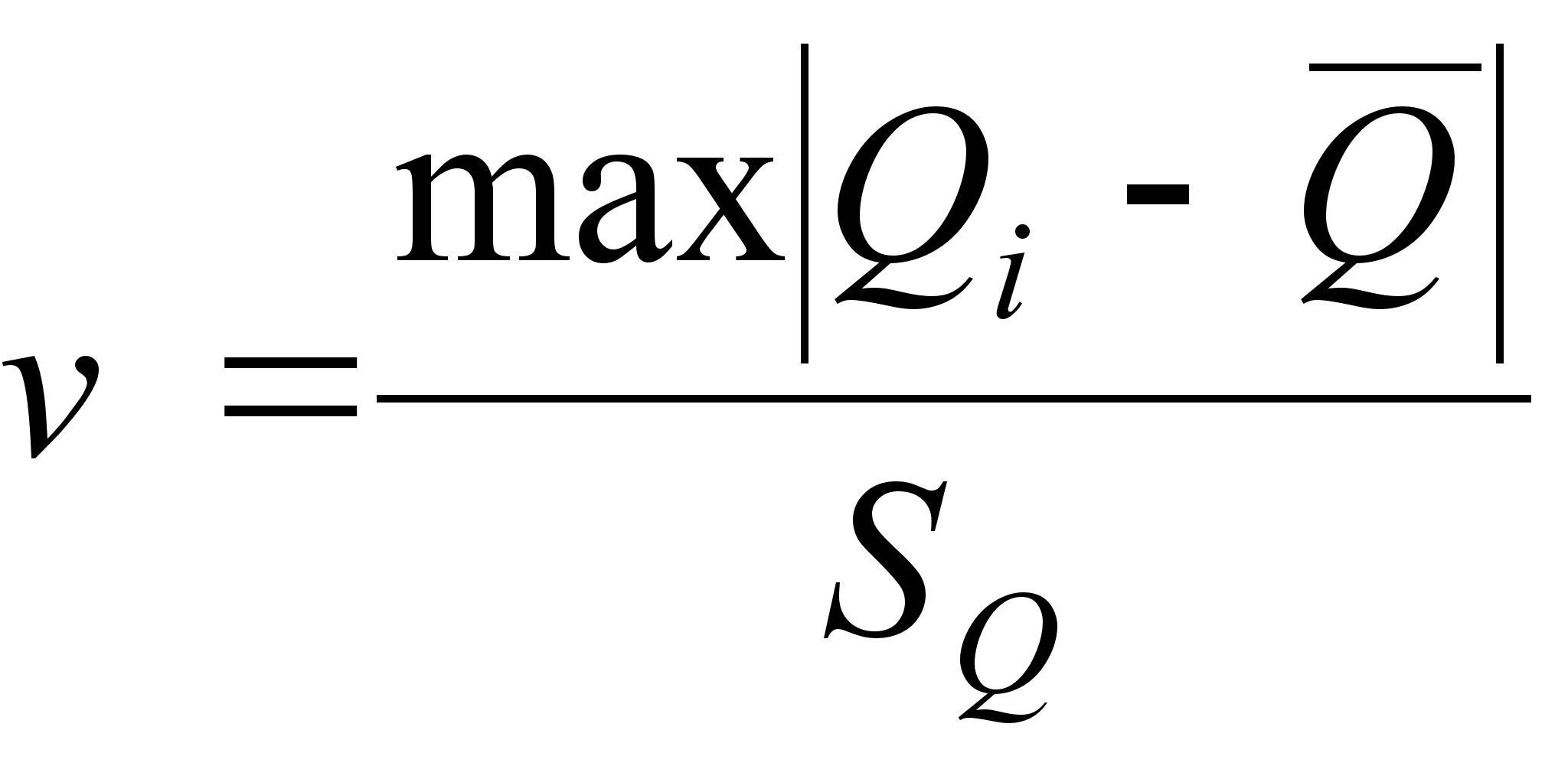 (5)
(5)
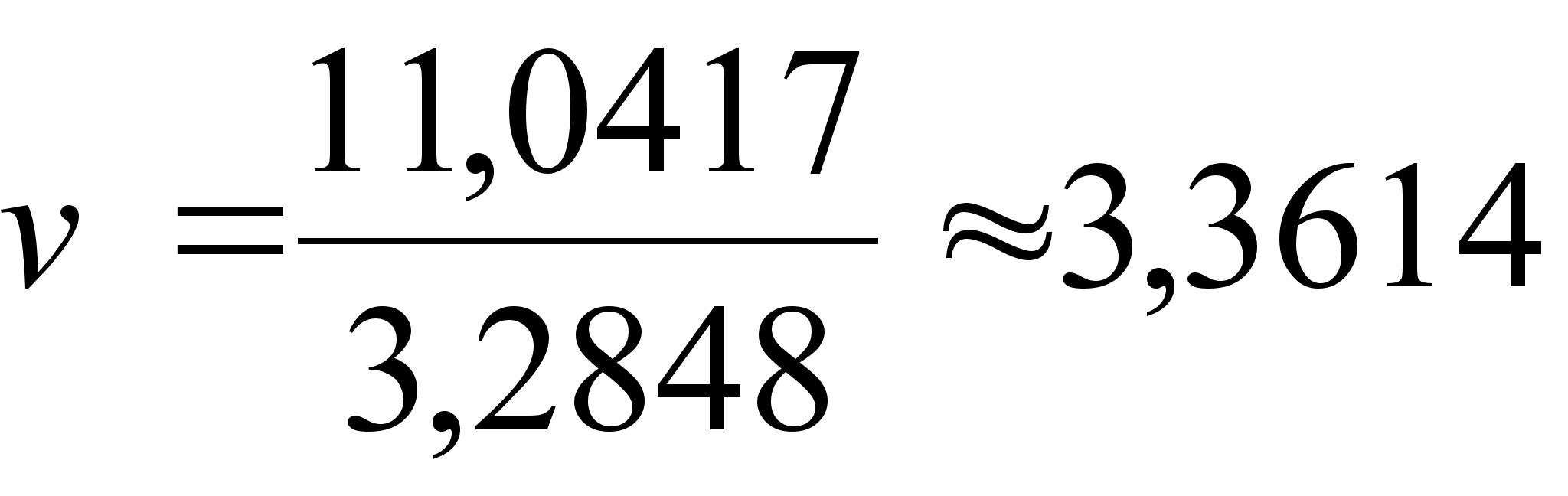
– задаемся
доверительной
вероятностью
P
= 0,95 и из соответствующих
таблиц (табл.
П6) с учетом q
= 1 – P
находим соответствующее
ей теоретическое
(табличное)
значение
![]() :
:
![]()
![]() при n
= 24;
при n
= 24;
– сравниваем
![]() с
с
![]() :
:
![]() .
Это означает,
что данный
результат
измерения Qi,
т.е. Q24
является ошибочным,
он должен быть
отброшен. Необходимо
повторить
вычисления
по п.п. 1 и 2 для
сокращенной
серии результатов
измерений и
проводить их
до тех пор, пока
не будет выполняться
условие
.
Это означает,
что данный
результат
измерения Qi,
т.е. Q24
является ошибочным,
он должен быть
отброшен. Необходимо
повторить
вычисления
по п.п. 1 и 2 для
сокращенной
серии результатов
измерений и
проводить их
до тех пор, пока
не будет выполняться
условие
![]() .
.
Повторяем вычисления, при этом отбрасываем измерение №24:
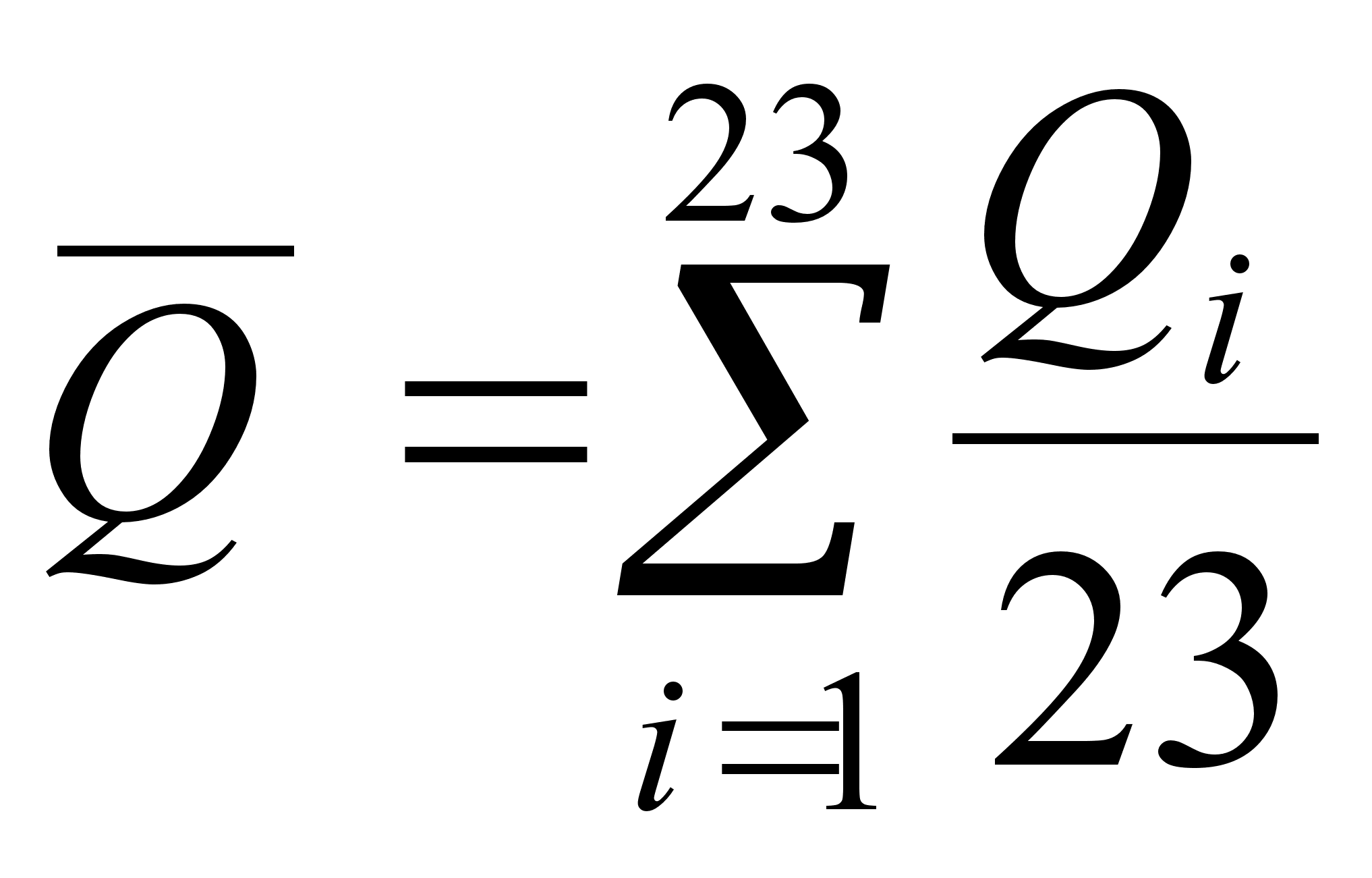
![]() (6)
(6)
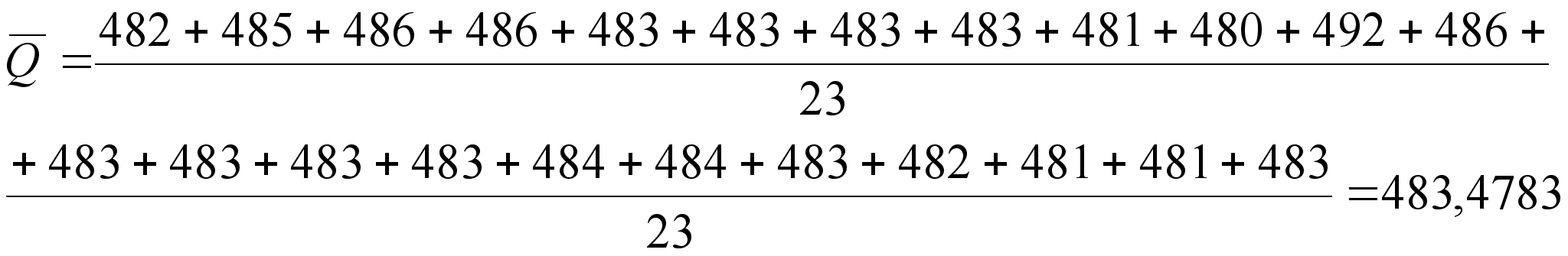
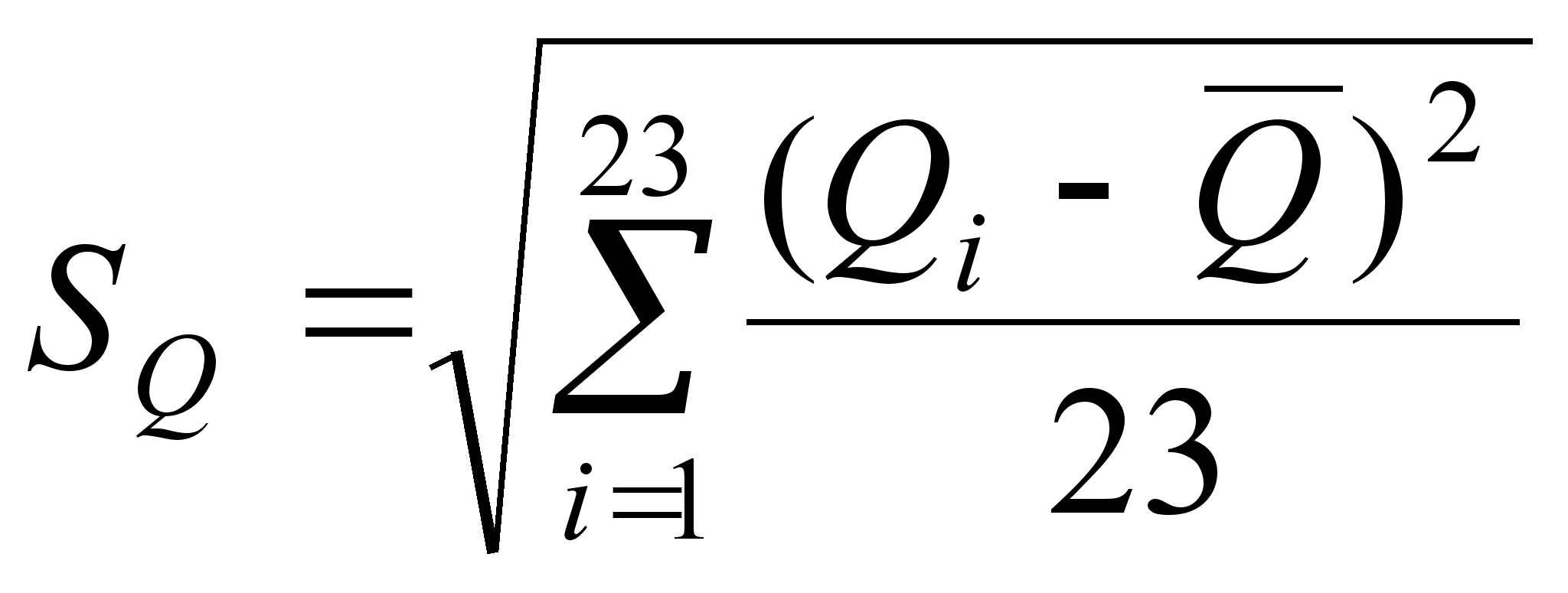 (7)
(7)
Таблица 3
| № из-мерения |
Результат измере-ния (Qi) |
|
|
№ из-мерения |
Результат измере-ния (Qi) |
|
|
| 1 | 482 | -1,4783 | 2,1853 | 13 | 483 | -0,4783 | 0,2287 |
| 2 | 485 | 1,5217 | 2,3157 | 14 | 483 | -0,4783 | 0,2287 |
| 3 | 486 | 2,5217 | 6,3592 | 15 | 483 | -0,4783 | 0,2287 |
| 4 | 486 | 2,5217 | 6,3592 | 16 | 483 | -0,4783 | 0,2287 |
| 5 | 483 | -0,4783 | 0,2287 | 17 | 484 | 0,5217 | 0,2722 |
| 6 | 483 | -0,4783 | 0,2287 | 18 | 484 | 0,5217 | 0,2722 |
| 7 | 483 | -0,4783 | 0,2287 | 19 | 483 | -0,4783 | 0,2287 |
| 8 | 483 | -0,4783 | 0,2287 | 20 | 482 | -1,4783 | 2,1853 |
| 9 | 481 | -2,4783 | 6,1418 | 21 | 481 | -2,4783 | 6,1418 |
| 10 | 480 | -3,4783 | 12,0983 | 22 | 481 | -2,4783 | 6,1418 |
| 11 | 492 | 8,5217 | 72,6200 | 23 | 483 | -0,4783 | 0,2287 |
| 12 | 486 | 2,5217 | 6,3592 |
Σ |
0 |
131,7391 |
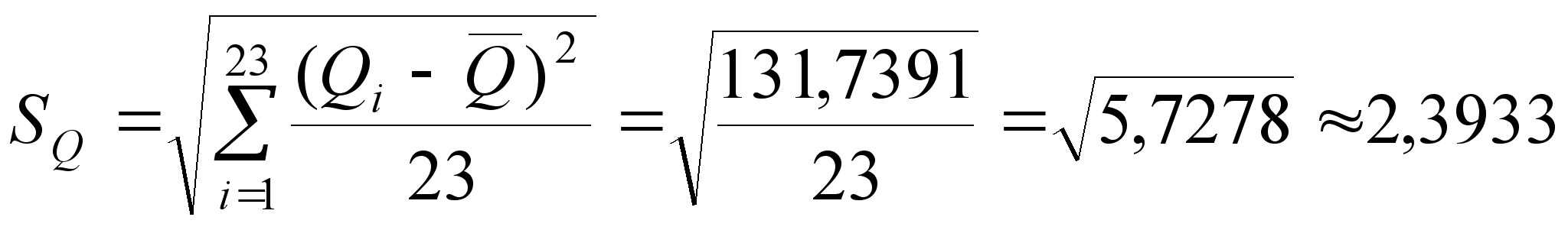
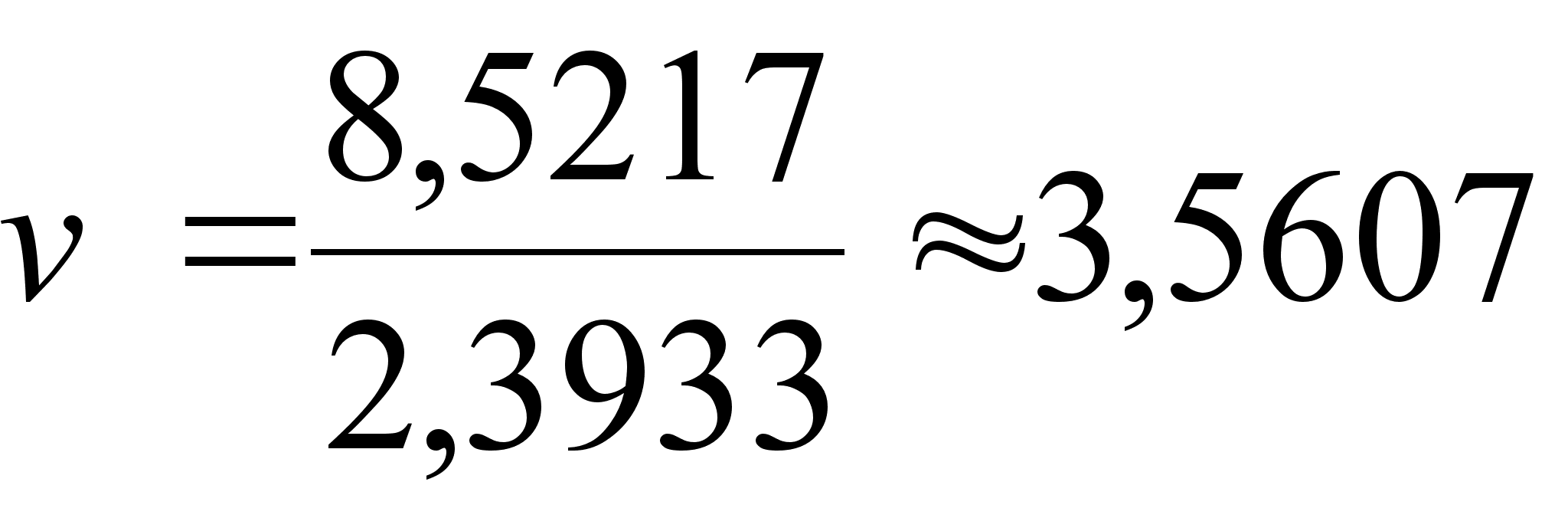
![]() при n
= 23;
при n
= 23;
Сравниваем
![]() с
с
![]() :
:
![]() .
Отбрасываем
измерение №11
и повторяем
вычисления.
.
Отбрасываем
измерение №11
и повторяем
вычисления.
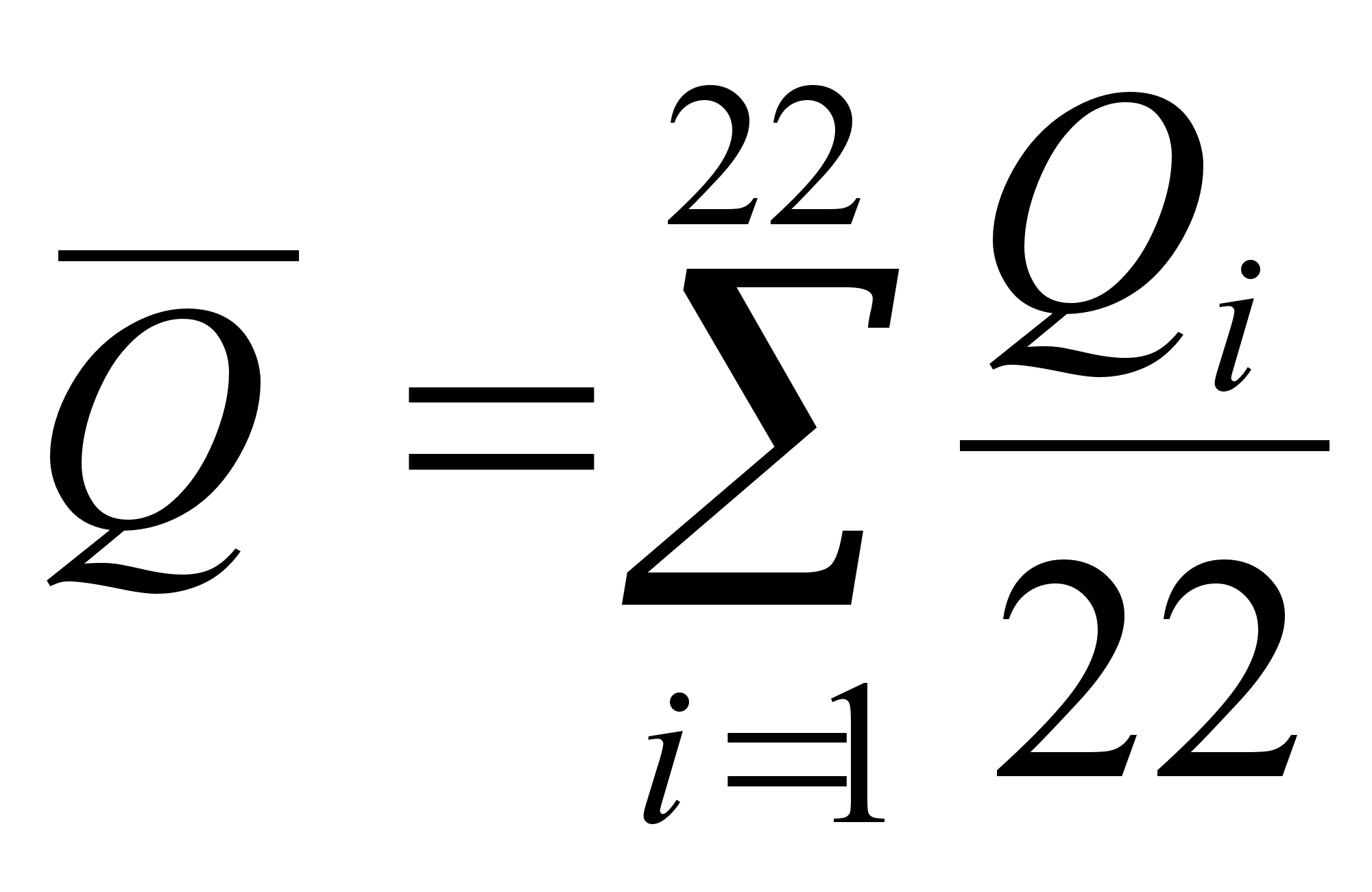
![]() (8)
(8)
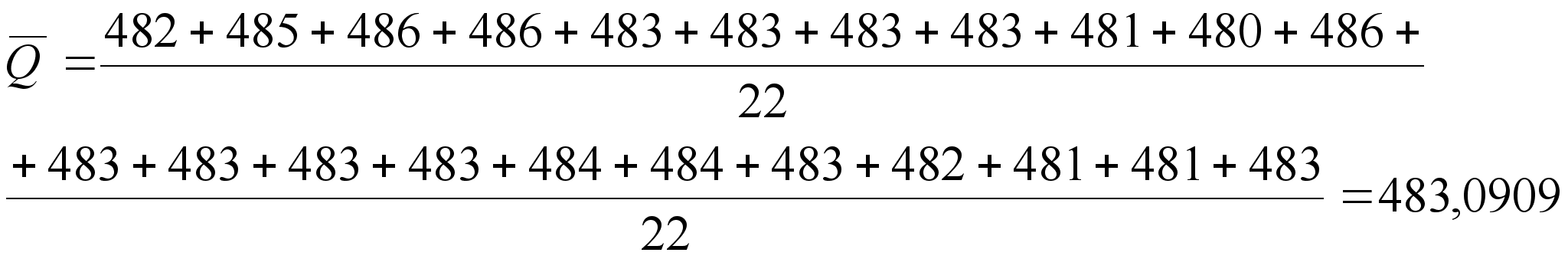
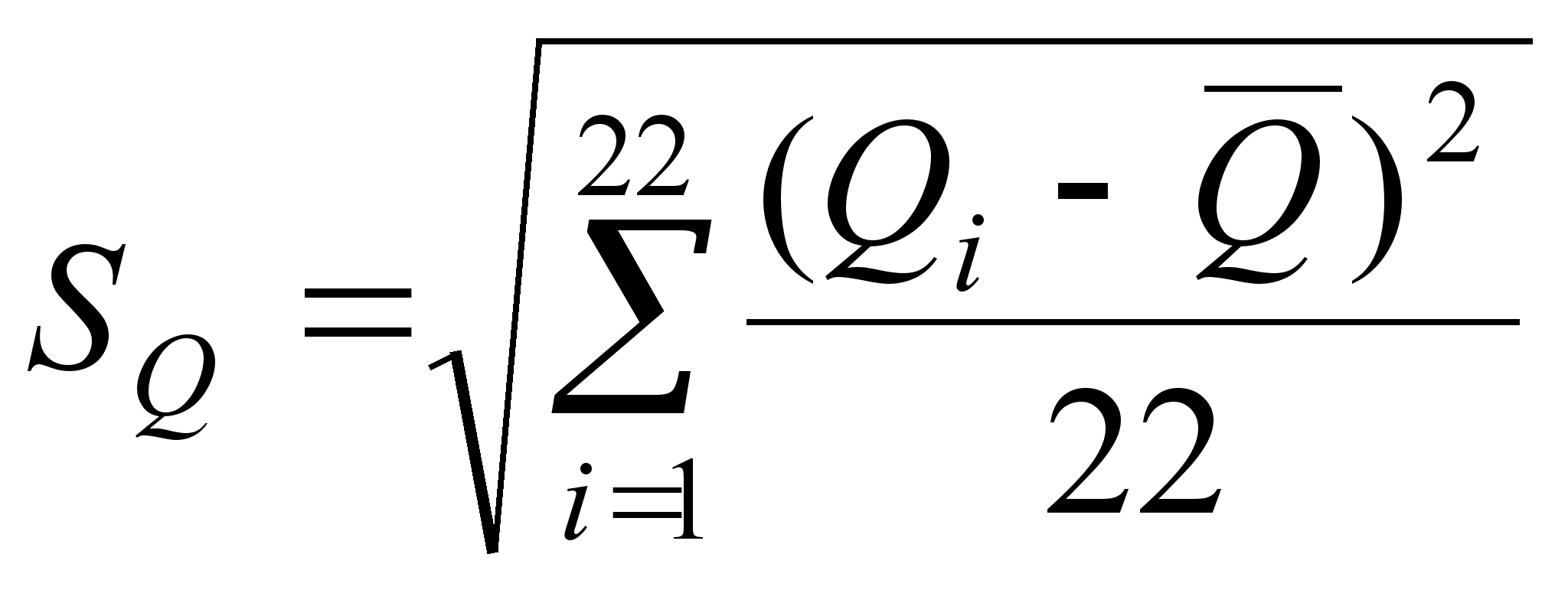 (9)
(9)
Таблица 4
| № из-мерения |
Результат измере-ния (Qi) |
|
|
№ из-мерения |
Результат измере-ния (Qi) |
|
|
| 1 | 482 | -1,0909 | 1,1901 | 12 | 483 | -0,0909 | 0,0083 |
| 2 | 485 | 1,9091 | 3,6446 | 13 | 483 | -0,0909 | 0,0083 |
| 3 | 486 | 2,9091 | 8,4628 | 14 | 483 | -0,0909 | 0,0083 |
| 4 | 486 | 2,9091 | 8,4628 | 15 | 483 | -0,0909 | 0,0083 |
| 5 | 483 | -0,0909 | 0,0083 | 16 | 484 | 0,9091 | 0,8264 |
| 6 | 483 | -0,0909 | 0,0083 | 17 | 484 | 0,9091 | 0,8264 |
| 7 | 483 | -0,0909 | 0,0083 | 18 | 483 | -0,0909 | 0,0083 |
| 8 | 483 | -0,0909 | 0,0083 | 19 | 482 | -1,0909 | 1,1901 |
| 9 | 481 | -2,0909 | 4,3719 | 20 | 481 | -2,0909 | 4,3719 |
| 10 | 480 | -3,0909 | 9,5537 | 21 | 481 | -2,0909 | 4,3719 |
| 11 | 486 | 2,9091 | 8,4628 | 22 | 483 | -0,0909 | 0,0083 |
|
Σ |
0 |
55,8182 |
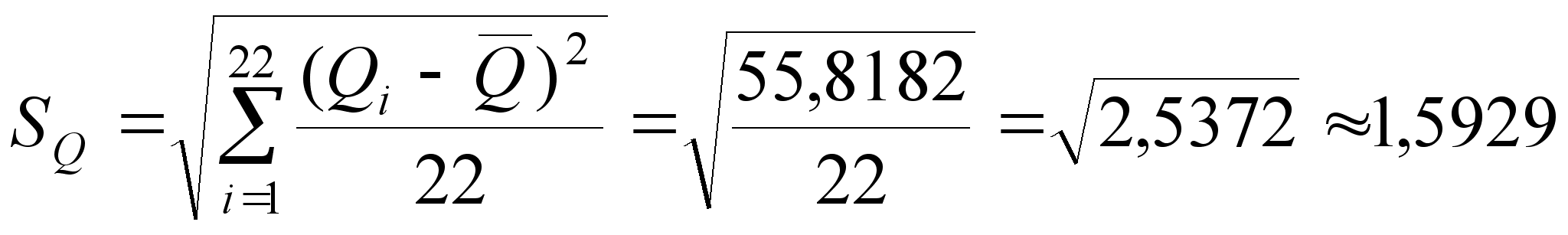
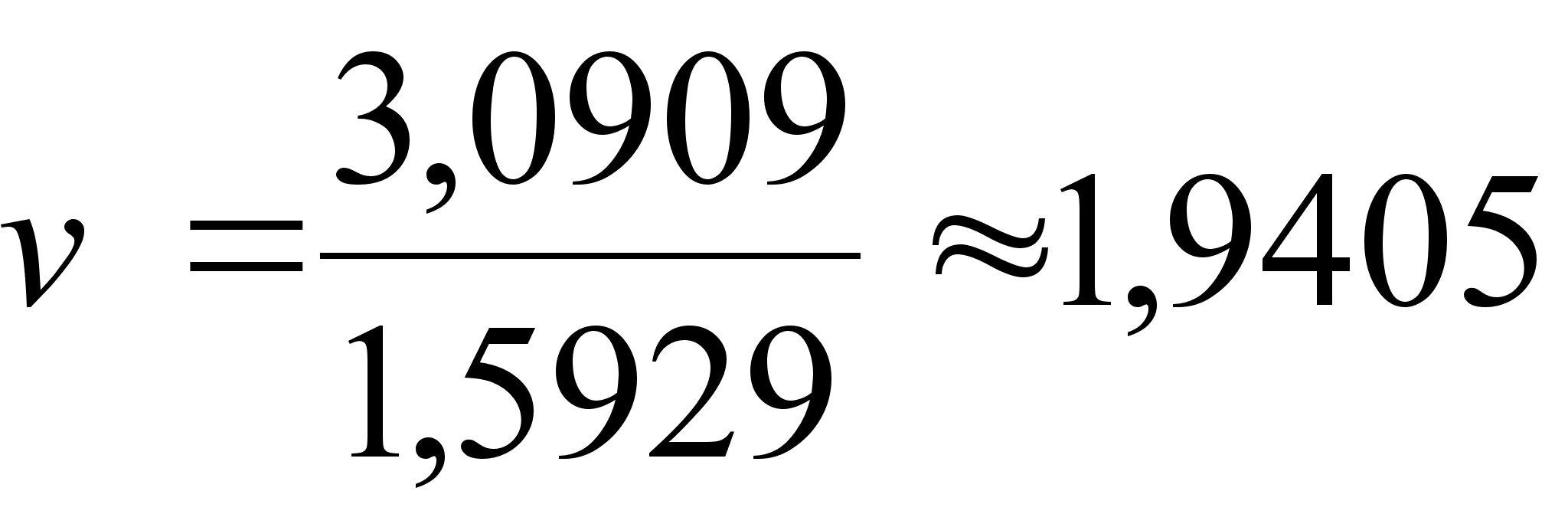
![]() при n
= 22;
при n
= 22;
Сравниваем
![]() с
с
![]() .
Так как
.
Так как
![]() ,
то результат
измерения №10
не является
ошибочным и
окончательно
остается 22
измерения, т.е.
n
= 22.
,
то результат
измерения №10
не является
ошибочным и
окончательно
остается 22
измерения, т.е.
n
= 22.
3. Проверяем гипотезу о нормальности распределения оставшихся результатов измерений.
– Применяем критерий 1, вычисляем отношение
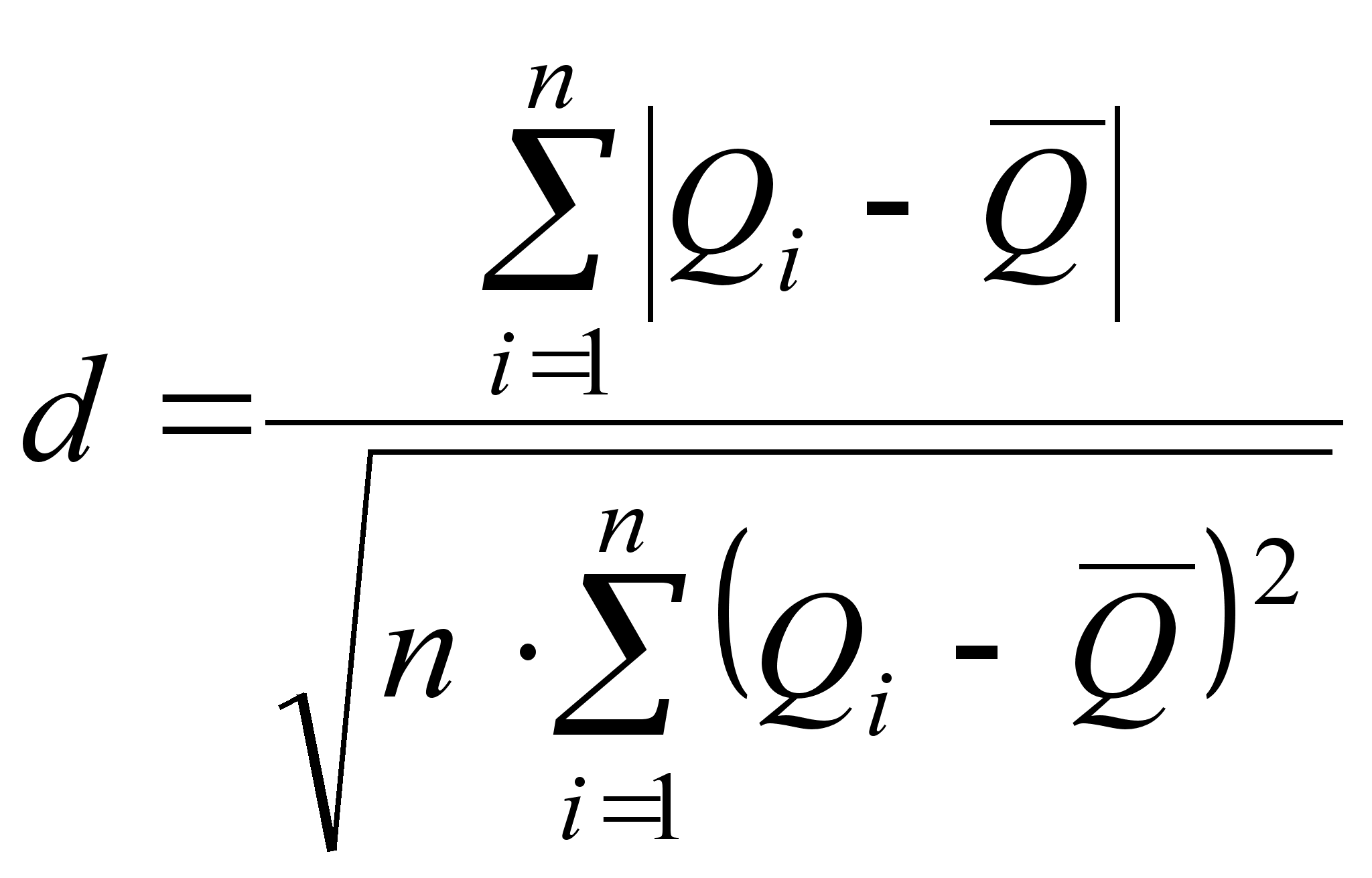 (10)
(10)
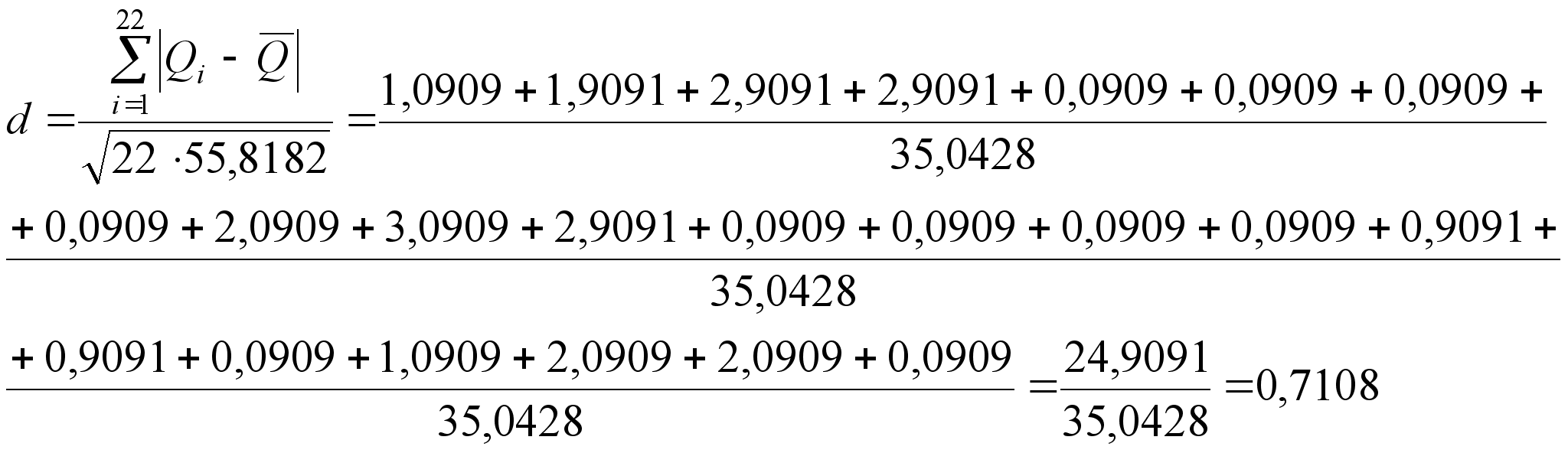
– задаемся
доверительной
вероятностью
P1
= 0,99 и для уровня
значимости
q1
= 1 – P1
по таблице П7
определяем
квантили
распределения
![]() и
и
![]() ,
,
![]() ,
,
![]() для
n
= 22.
для
n
= 22.
– сравниваем
![]() с
с
![]() и
и
![]() :
:
![]() ,
значит гипотеза
о нормальном
законе распределения
вероятности
результата
измерения
согласуется
с экспериментальными
данными, т.е.
результаты
наблюдений
можно считать
распределенными
нормально.
,
значит гипотеза
о нормальном
законе распределения
вероятности
результата
измерения
согласуется
с экспериментальными
данными, т.е.
результаты
наблюдений
можно считать
распределенными
нормально.
Так как n > 15, применяем критерий 2.
– задаемся доверительной вероятностью P2 = 0,98 и для уровня значимости q2 = 1 – P2 с учетом n = 22 определяем по таблице П8 значения m и P*. m = 2; P* = 0,97.
– для вероятности P* из таблиц для интегральной функции нормированного нормального распределения Ф(t) определяем значение t:
![]() ;
(11)
;
(11)
при Ф(t) = 0,485 t = 2,17;
Рассчитываем E:
![]() ; (12)
; (12)
![]() ;
;
Согласно
критерию 2 результаты
наблюдений
принадлежат
нормальному
закону распределения,
если не более
m
разностей
![]() превысили E.
Из таблицы 4
видно, что ни
одна разность
превысили E.
Из таблицы 4
видно, что ни
одна разность
![]() не превышает
E
= 3,4566. Следовательно,
гипотеза о
нормальном
законе распределения
вероятности
результата
измерения
согласуется
с экспериментальными
данными.
не превышает
E
= 3,4566. Следовательно,
гипотеза о
нормальном
законе распределения
вероятности
результата
измерения
согласуется
с экспериментальными
данными.
Соблюдаются
оба критерия,
значит закон
можно признать
нормальным
с вероятностью
![]() ,
,
![]() .
.
4. Определяем стандартное отклонение среднего арифметического.
Так как закон распределения вероятности результата измерений признан нормальным, то стандартное отклонение определяем как:
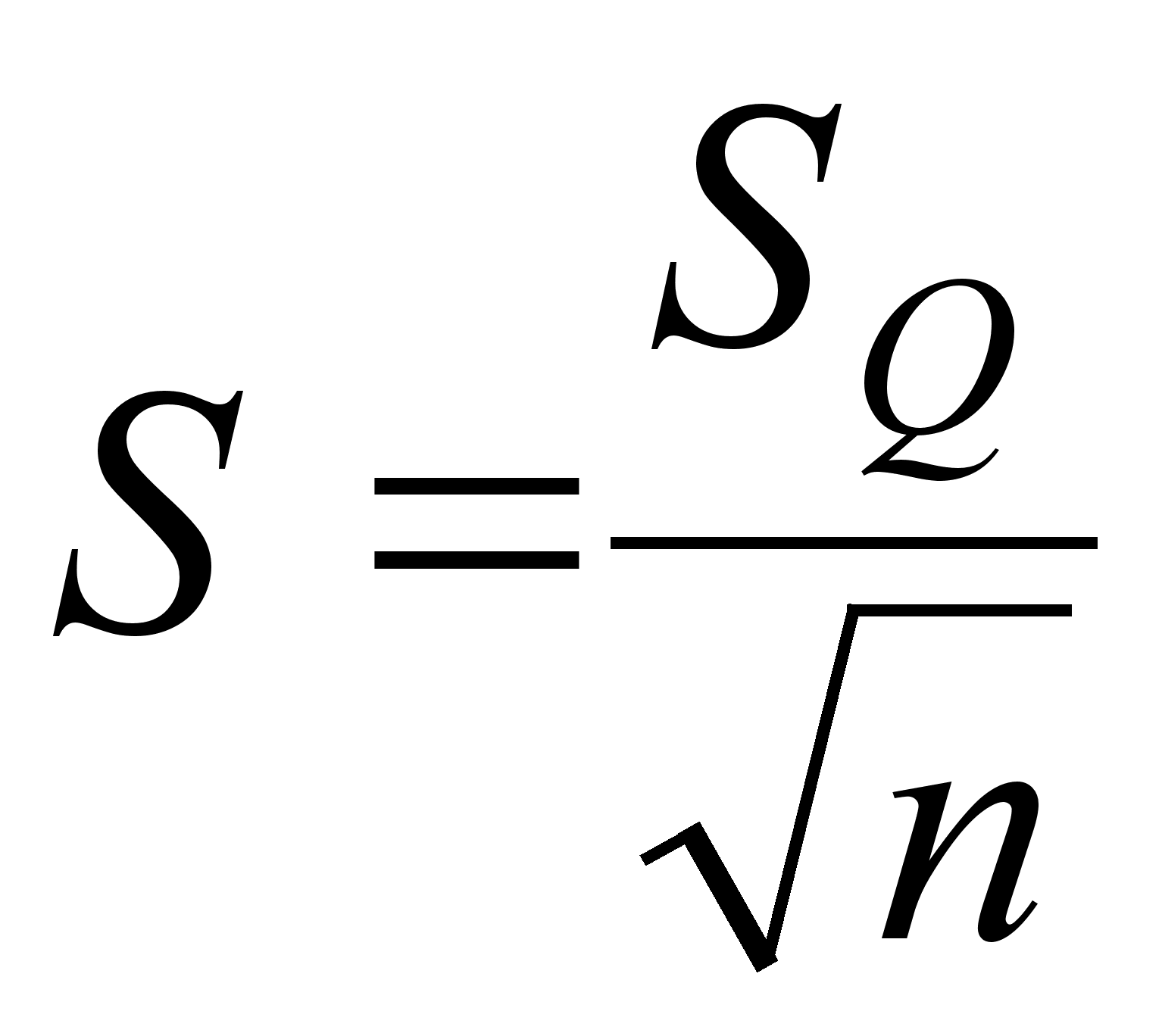 (13)
(13)
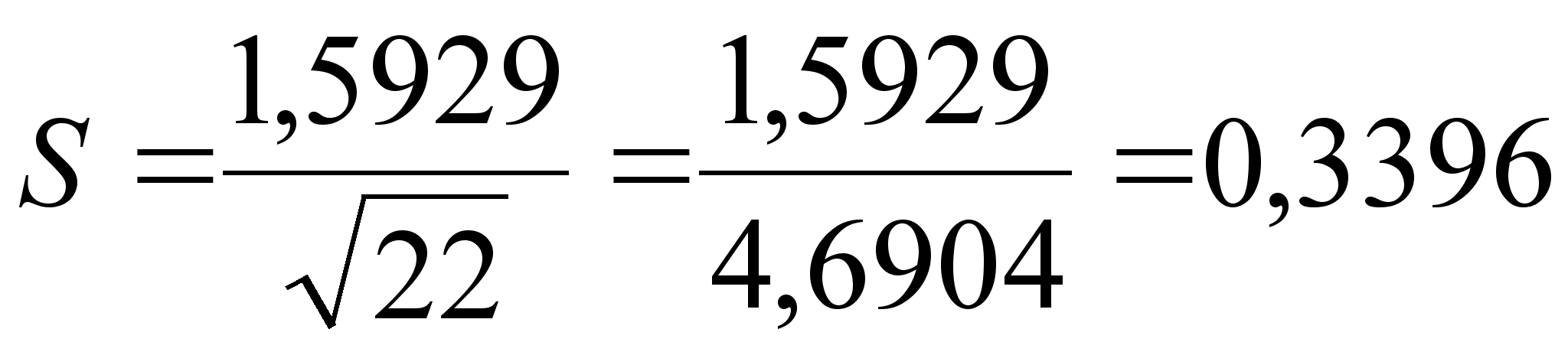
5. Определяем доверительный интервал.
Закон распределения вероятности результата измерений признан нормальным, поэтому доверительный интервал для заданной доверительной вероятности P определяется из распределения Стьюдента.
P
= 0,98;
![]() ;
t
= 2,33;
;
t
= 2,33;
![]() ;
(14)
;
(14)
Значение Q будет находиться в пределах:
![]()
![]()
3. Обработка результатов нескольких серий измерений
Условие. При многократных измерениях одной и той же величины получены две серии по 12 (nj) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице 5. Вычислить результат многократных измерений.
Исходные данные:
Таблица 5
| Серия 1 | Серия 2 | ||||||
| № изме-рения | Результат измерения | № изме-рения | Результат измерения | № изме-рения | Результат измерения | № изме-рения | Результат измерения |
| 1 | 482 | 7 | 483 | 1 | 483 | 7 | 483 |
| 2 | 485 | 8 | 483 | 2 | 483 | 8 | 482 |
| 3 | 486 | 9 | 481 | 3 | 483 | 9 | 481 |
| 4 | 486 | 10 | 480 | 4 | 483 | 10 | 481 |
| 5 | 483 | 11 | 492 | 5 | 484 | 11 | 483 |
| 6 | 483 | 12 | 486 | 6 | 484 | 12 | 495 |
Расчет.
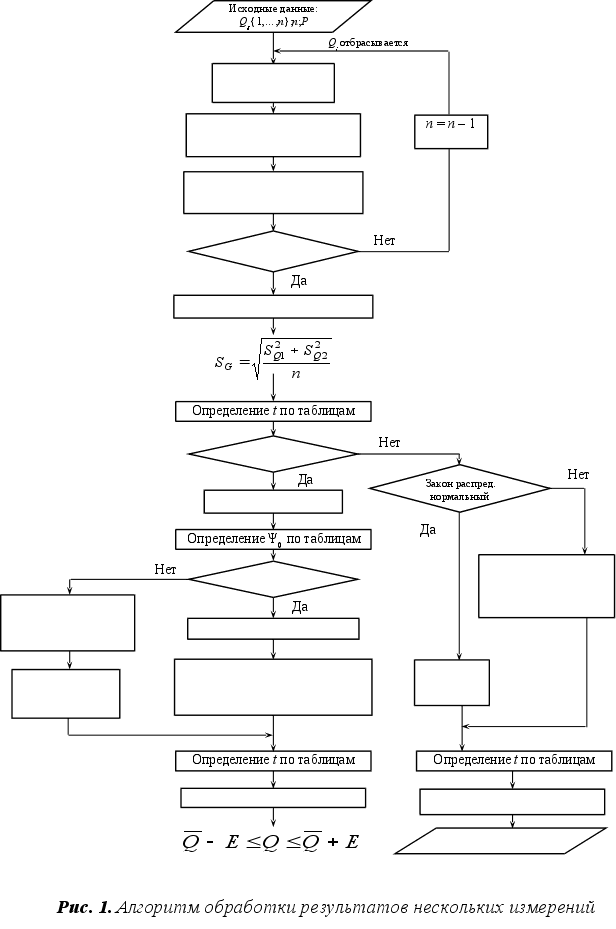
1. Обрабатываем экспериментальные данные по алгоритму, изложенному в п.п. 1–3 задания 2, при этом:
– определяем
оценки результата
измерения
![]() и среднеквадратического
отклонения
и среднеквадратического
отклонения
![]() ;
;
– обнаруживаем и исключаем ошибки;
– проверяем гипотезу о нормальности распределения оставшихся результатов измерений.
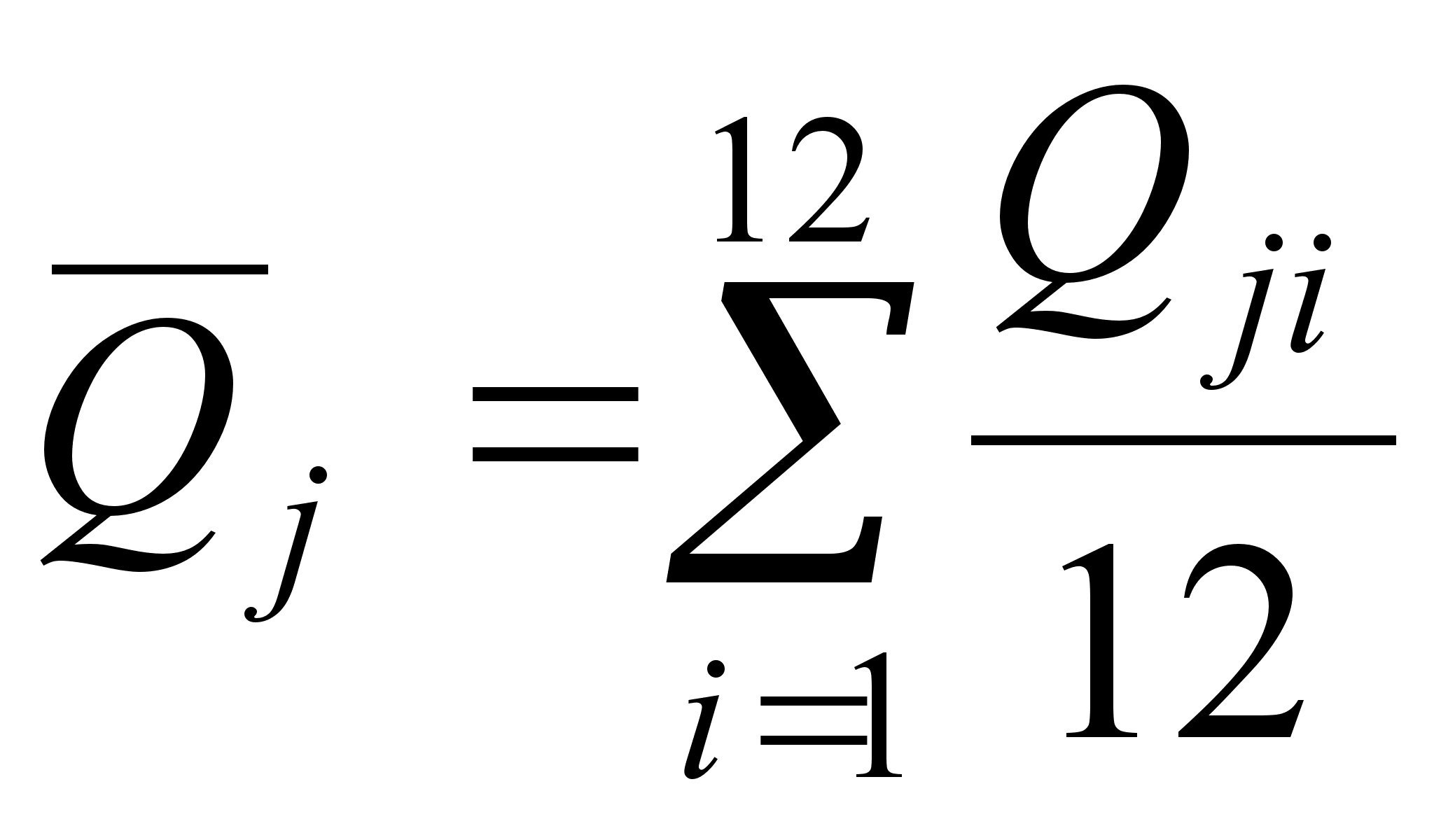
![]() (15)
(15)
![]()
![]()
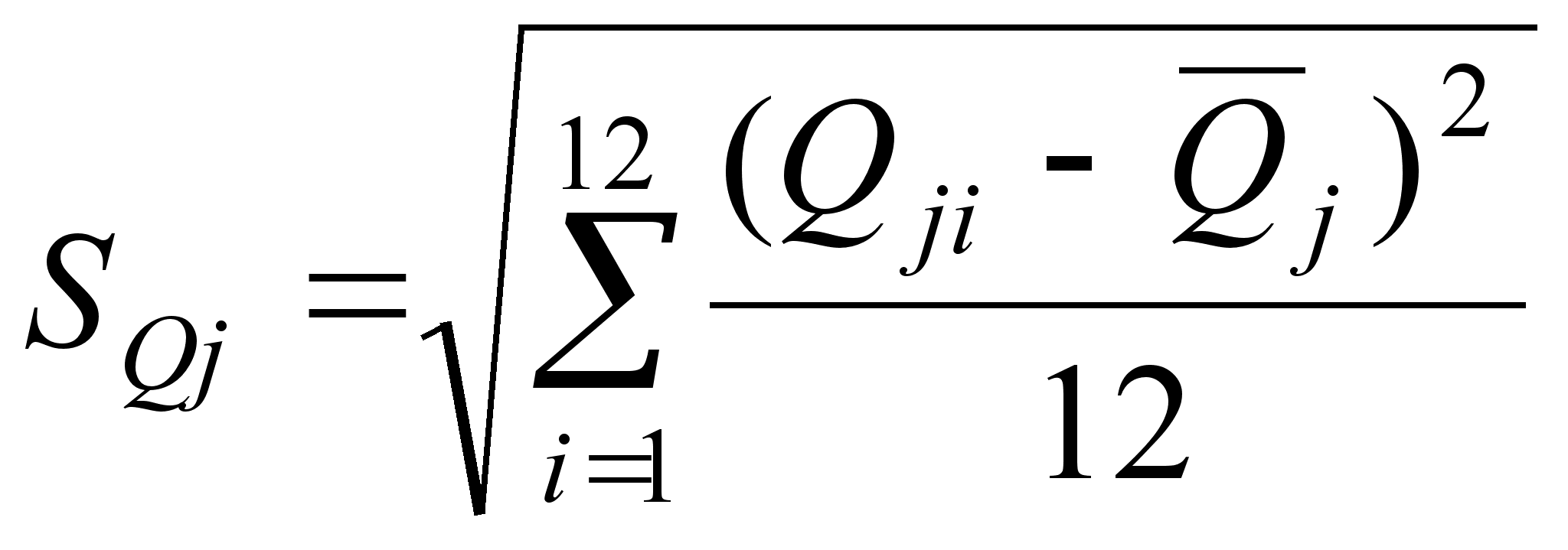 (16)
(16)
Таблица 6
| Серия 1 | Серия 2 | ||||||
| № из-мерения |
Результат измере-ния (Q1i) |
|
|
№ из-мерения |
Результат измере-ния (Q2i) |
|
|
| 1 | 482 | -2,1667 | 4,6944 | 1 | 483 | -0,7500 | 0,5625 |
| 2 | 485 | 0,8333 | 0,6944 | 2 | 483 | -0,7500 | 0,5625 |
| 3 | 486 | 1,8333 | 3,3611 | 3 | 483 | -0,7500 | 0,5625 |
| 4 | 486 | 1,8333 | 3,3611 | 4 | 483 | -0,7500 | 0,5625 |
| 5 | 483 | -1,1667 | 1,3611 | 5 | 484 | 0,2500 | 0,0625 |
| 6 | 483 | -1,1667 | 1,3611 | 6 | 484 | 0,2500 | 0,0625 |
| 7 | 483 | -1,1667 | 1,3611 | 7 | 483 | -0,7500 | 0,5625 |
| 8 | 483 | -1,1667 | 1,3611 | 8 | 482 | -1,7500 | 3,0625 |
| 9 | 481 | -3,1667 | 10,0278 | 9 | 481 | -2,7500 | 7,5625 |
| 10 | 480 | -4,1667 | 17,3611 | 10 | 481 | -2,7500 | 7,5625 |
| 11 | 492 | 7,8333 | 61,3611 | 11 | 483 | -0,7500 | 0,5625 |
| 12 | 486 | 1,8333 | 3,3611 | 12 | 495 | 11,2500 | 126,5625 |
|
Σ |
0 |
109,6667 |
Σ |
0 |
148,2500 |
||
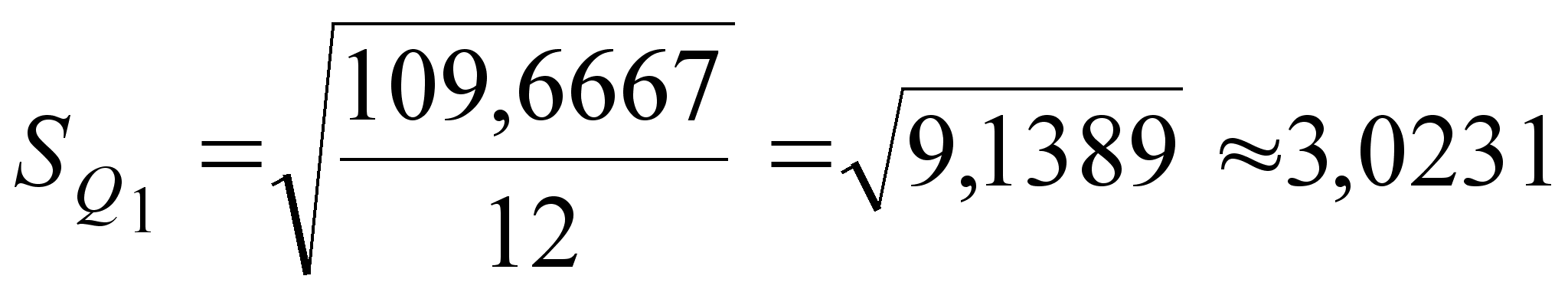 ;
;
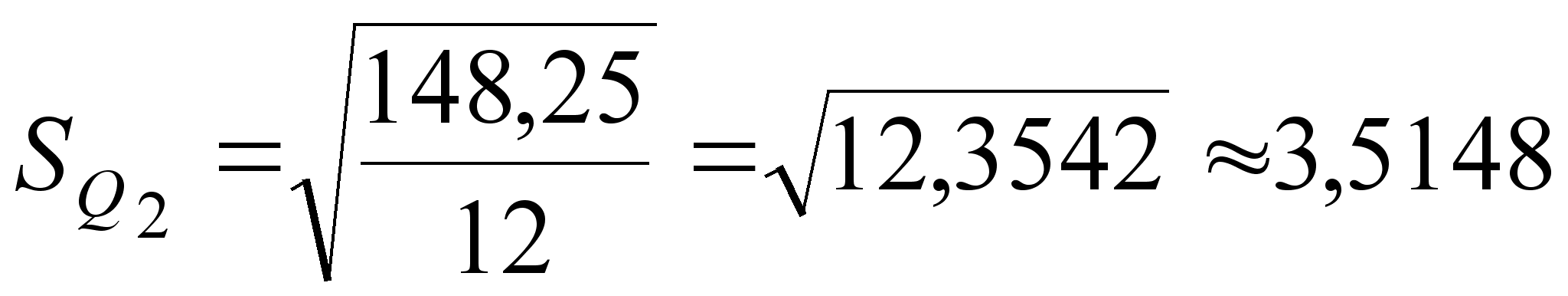
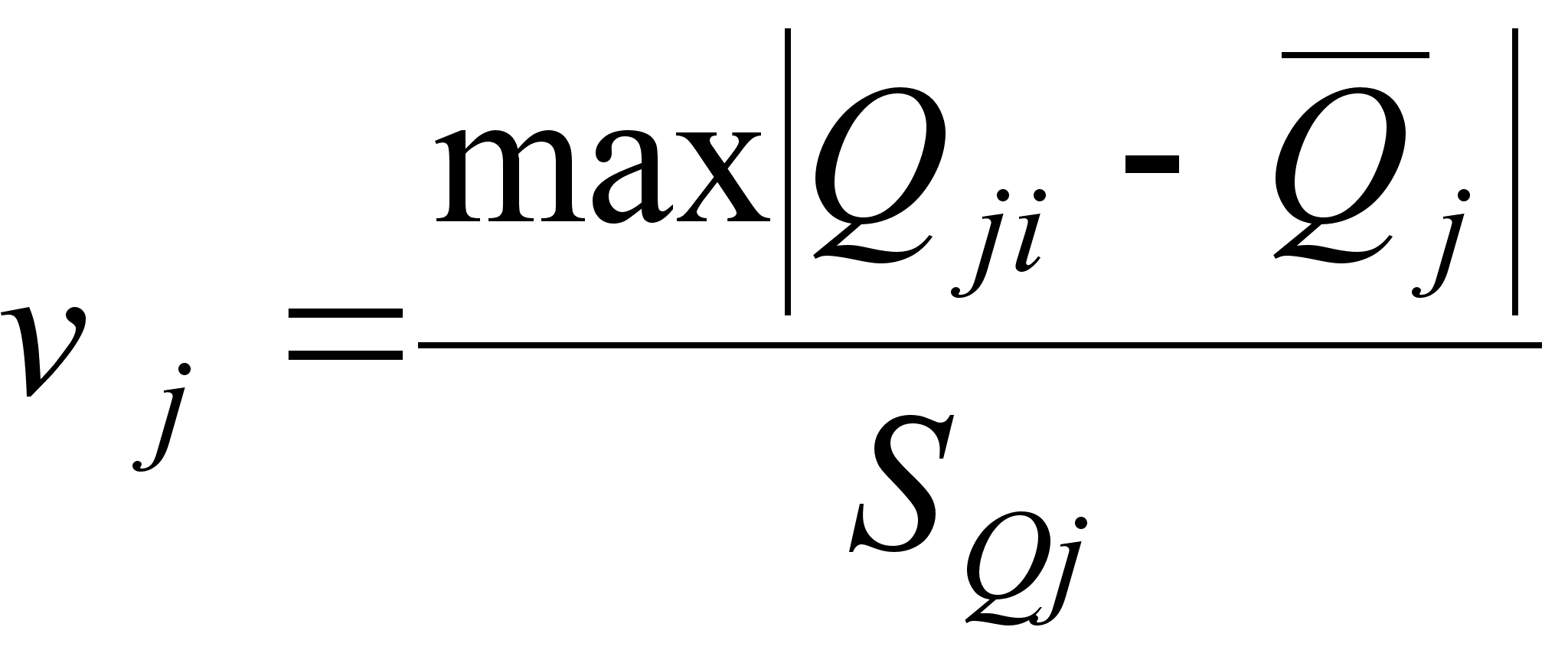 (17)
(17)
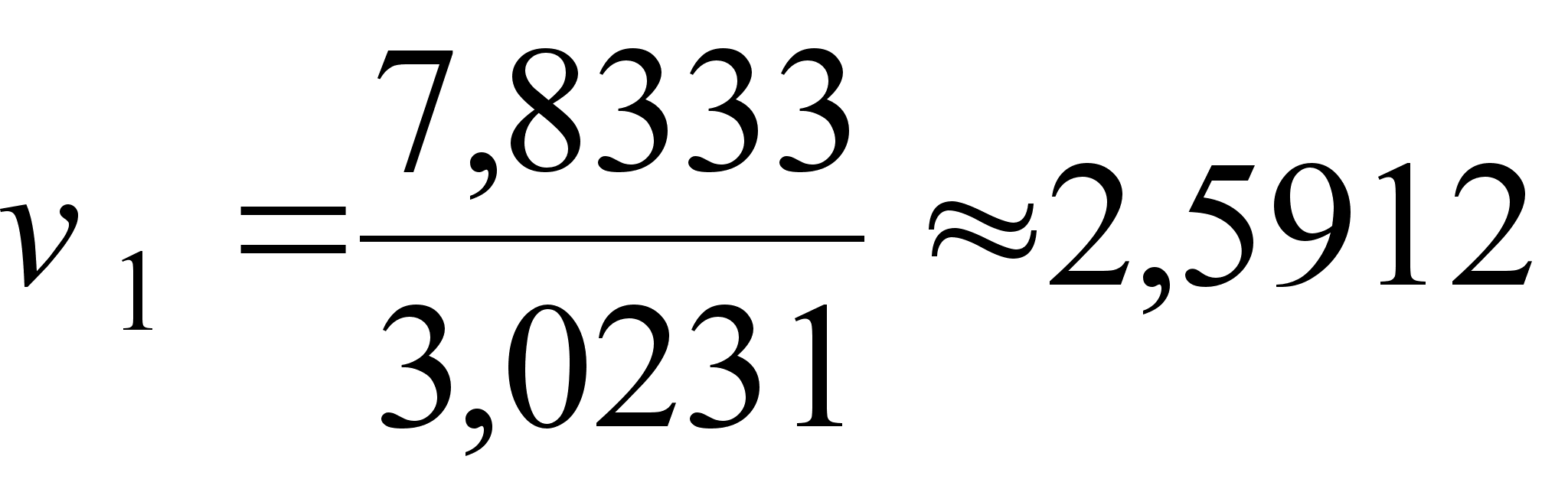 ;
;
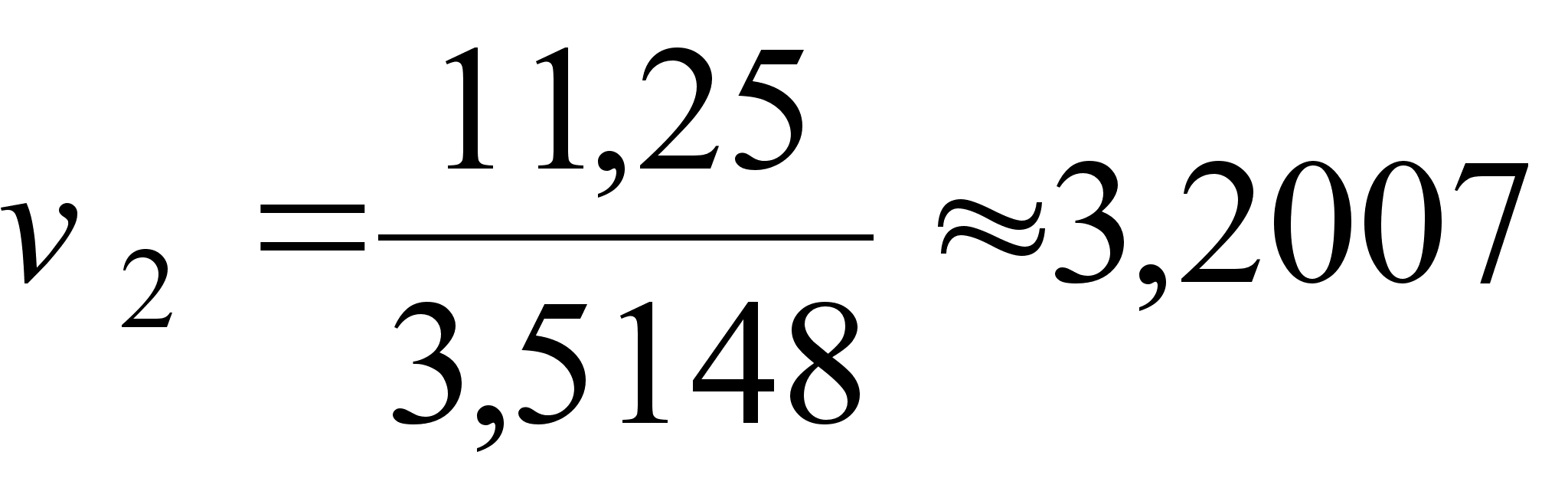 ;
;
![]() при n
= 12;
при n
= 12;
– сравниваем
![]() и
и
![]() с
с
![]() :
:
![]() и
и
![]() .
Результаты
измерения Q1,11
и Q2,12
являются ошибочными,
они должны быть
отброшены.
.
Результаты
измерения Q1,11
и Q2,12
являются ошибочными,
они должны быть
отброшены.
Повторяем вычисления, при этом отбрасываем измерения №1-11 и №2-12:
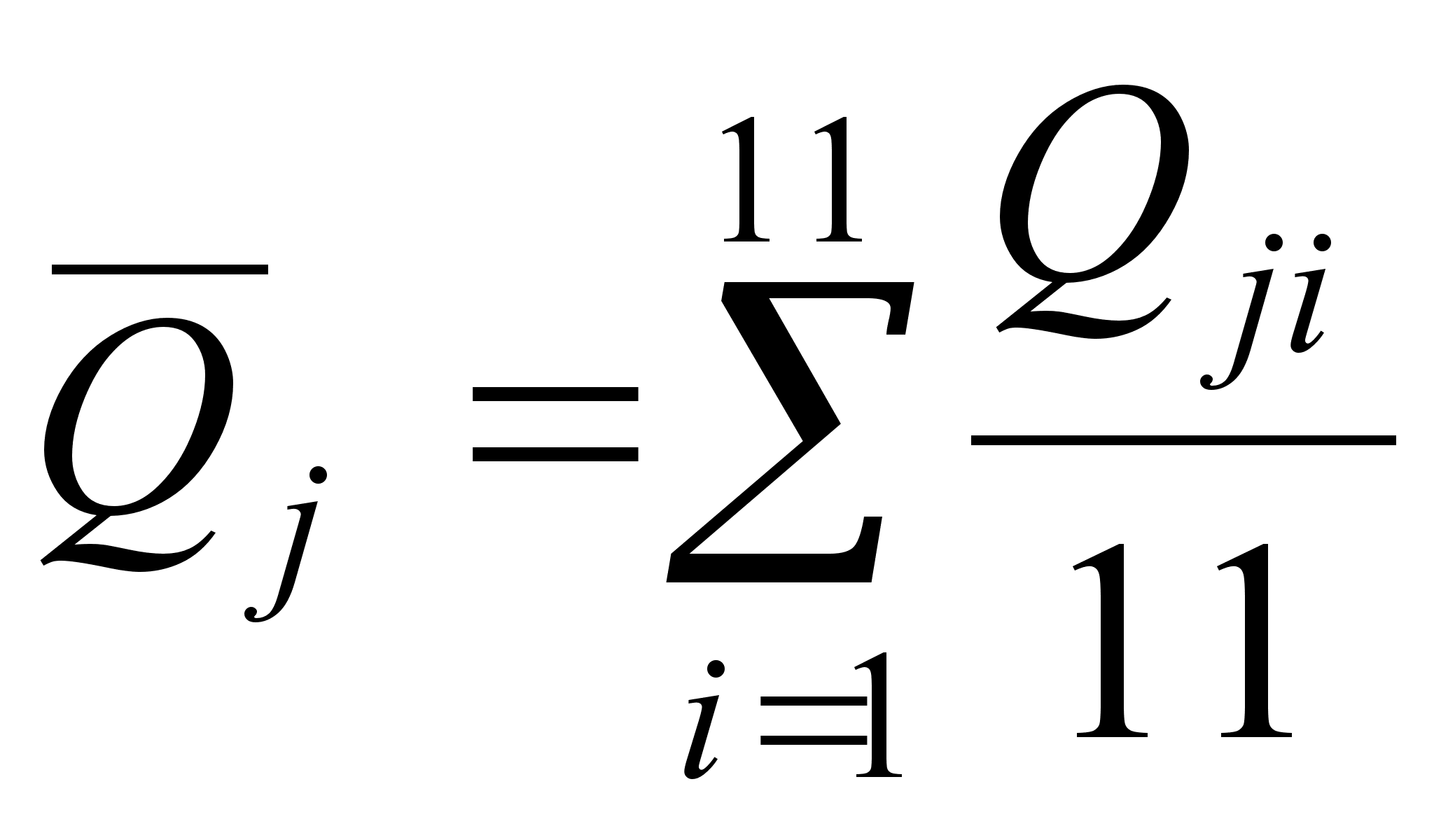 (18)
(18)
![]()
![]()
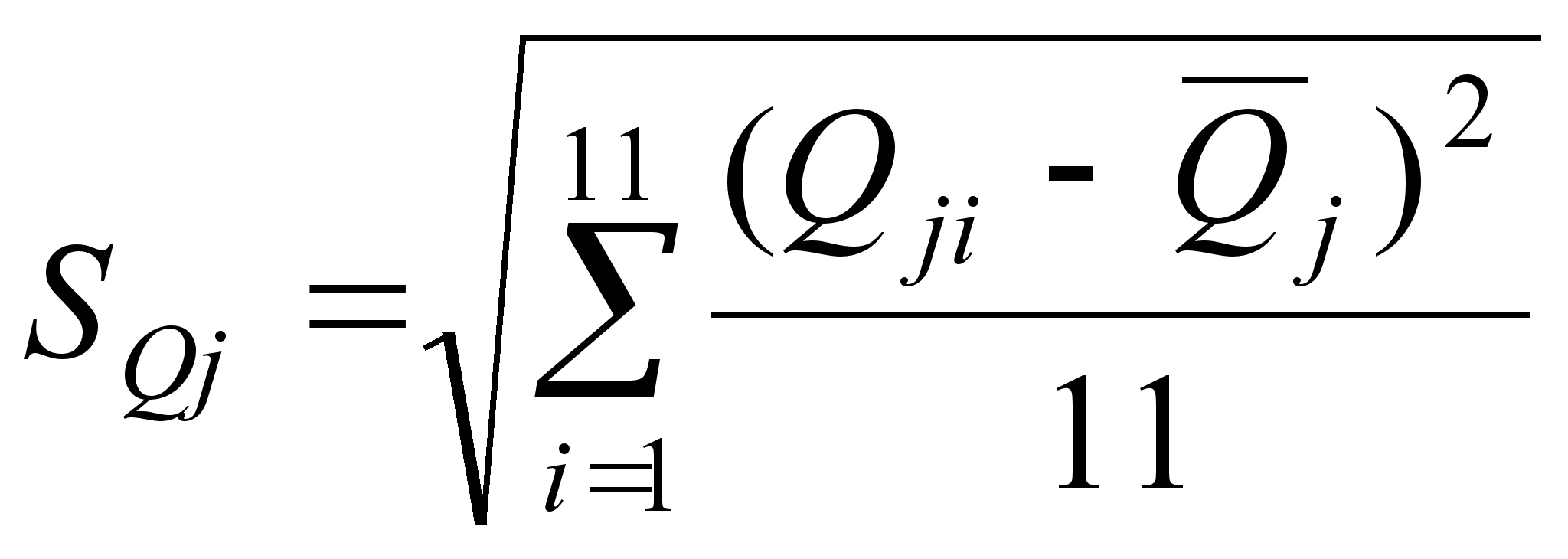 (19)
(19)
Таблица 7
| Серия 1 | Серия 2 | ||||||
| № из-мерения |
Результат измере-ния (Q1i) |
|
|
№ из-мерения |
Результат измере-ния (Q2i) |
|
|
| 1 | 482 | -1,4545 | 2,1157 | 1 | 483 | 0,2727 | 0,0744 |
| 2 | 485 | 1,5455 | 2,3884 | 2 | 483 | 0,2727 | 0,0744 |
| 3 | 486 | 2,5455 | 6,4793 | 3 | 483 | 0,2727 | 0,0744 |
| 4 | 486 | 2,5455 | 6,4793 | 4 | 483 | 0,2727 | 0,0744 |
| 5 | 483 | -0,4545 | 0,2066 | 5 | 484 | 1,2727 | 1,6198 |
| 6 | 483 | -0,4545 | 0,2066 | 6 | 484 | 1,2727 | 1,6198 |
| 7 | 483 | -0,4545 | 0,2066 | 7 | 483 | 0,2727 | 0,0744 |
| 8 | 483 | -0,4545 | 0,2066 | 8 | 482 | -0,7273 | 0,5289 |
| 9 | 481 | -2,4545 | 6,0248 | 9 | 481 | -1,7273 | 2,9835 |
| 10 | 480 | -3,4545 | 11,9339 | 10 | 481 | -1,7273 | 2,9835 |
| 11 | 486 | 2,5455 | 6,4793 | 11 | 483 | 0,2727 | 0,0744 |
|
Σ |
0 |
42,7273 |
Σ |
0 |
10,1818 |
||
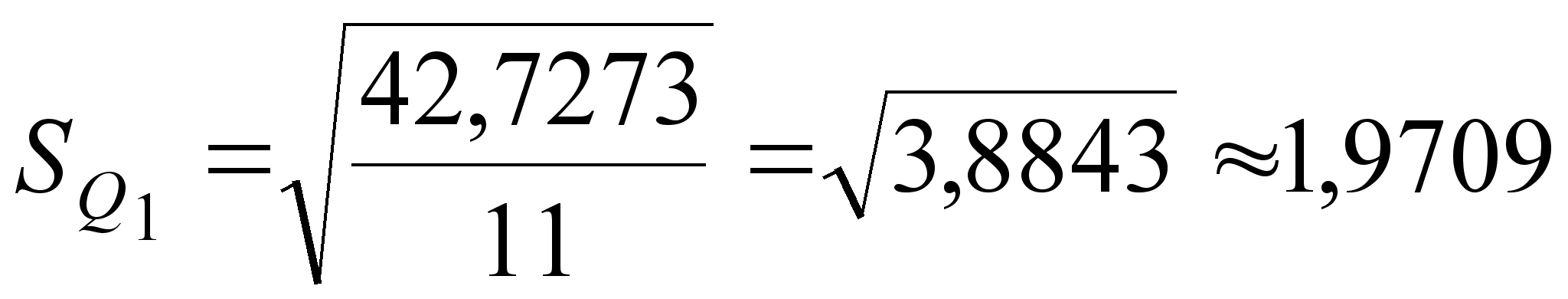 ;
;
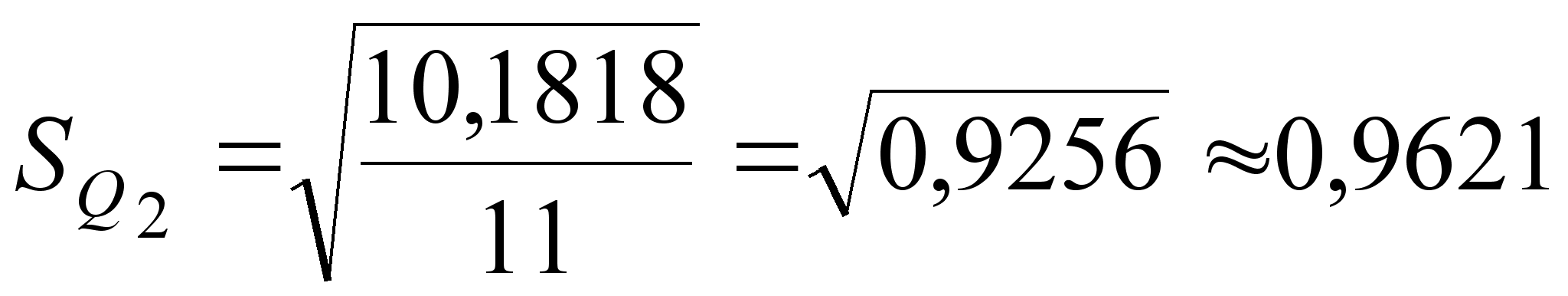
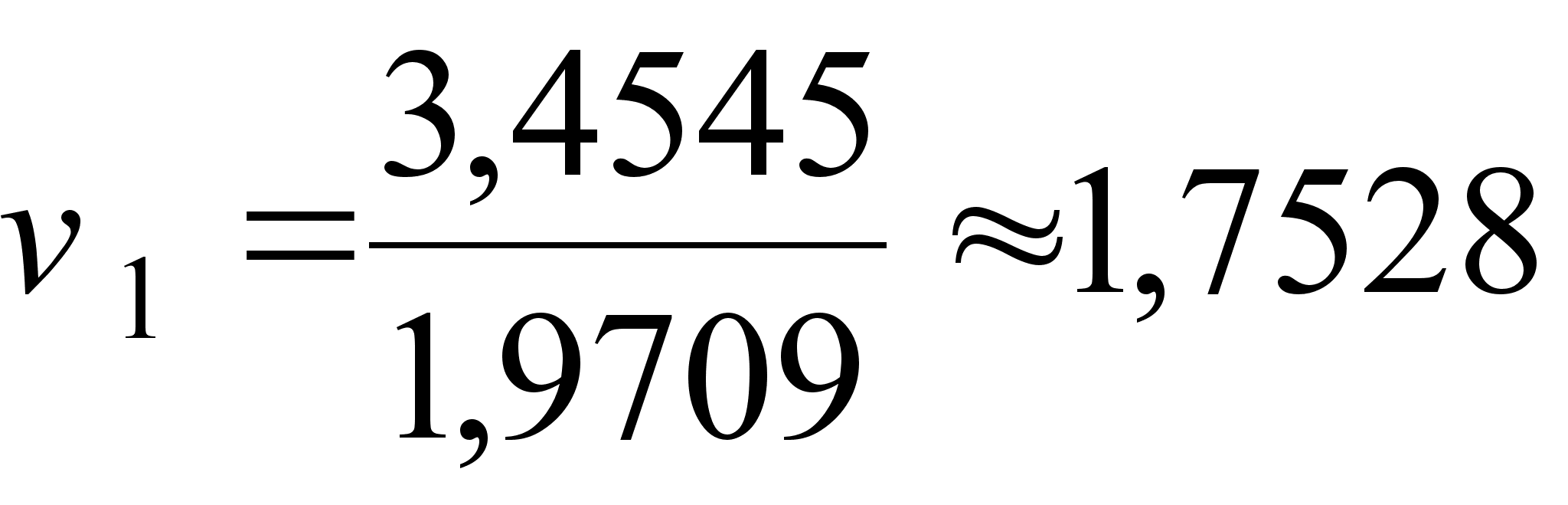 ;
;
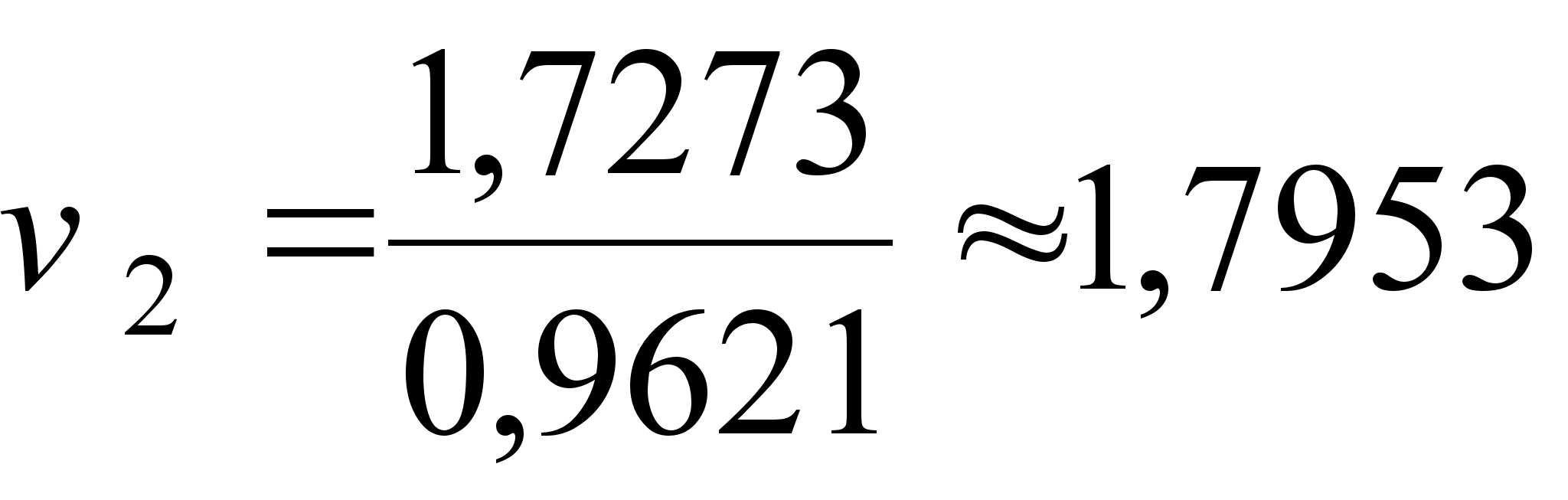 ;
;
![]() при n
= 11;
при n
= 11;
Сравниваем
![]() и
и
![]() с
с
![]() :
:
![]() и
и
![]() .
Результаты
измерений №1 10
и №2-9 не являются
ошибочными
и окончательно
остается 11 измерений
для обоих серий
измерений, т.е.
n
= 11.
.
Результаты
измерений №1 10
и №2-9 не являются
ошибочными
и окончательно
остается 11 измерений
для обоих серий
измерений, т.е.
n
= 11.
– Так
как n
![]() .
.
2. Проверяем значимость различия средних арифметических серий. Для этого:
– вычисляем моменты закона распределения разности:
![]() ,
(21)
,
(21)
![]()
n1 = n2 = n
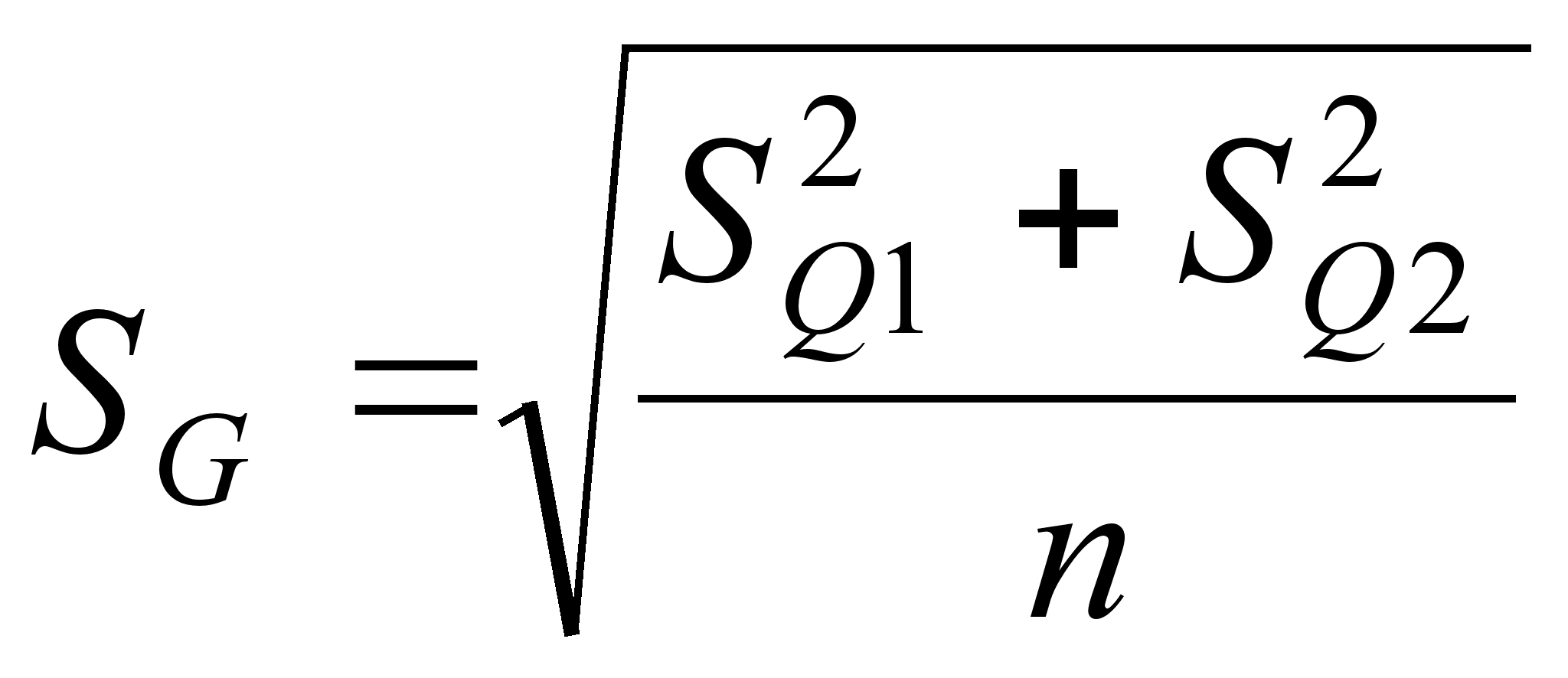 (22)
(22)
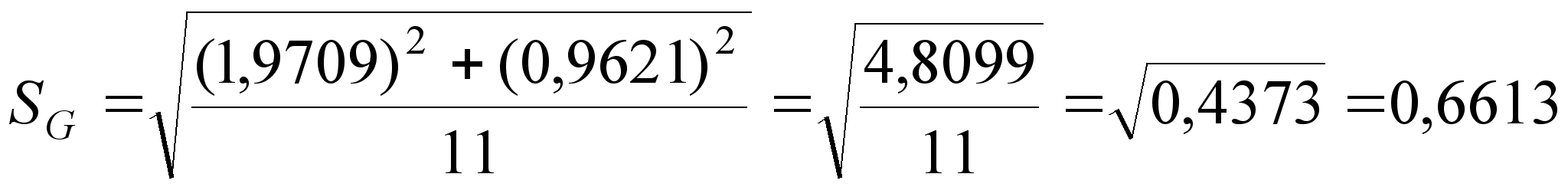
– задавшись доверительной вероятностью P = 0,95, определяем из таблицы интегральной функции нормированного нормального распределения Ф(t) значение t.
![]()
t = 1,645
– сравниваем
![]() с
с
![]() ,
,
![]() .
.
![]()
![]() .
Различия между
средними
арифметическими
в сериях с
доверительной
вероятностью
P
можно признать
незначимым
.
Различия между
средними
арифметическими
в сериях с
доверительной
вероятностью
P
можно признать
незначимым
3. Проверим равнорассеянность результатов измерений в сериях, для этого:
– определяем значение Ψ:
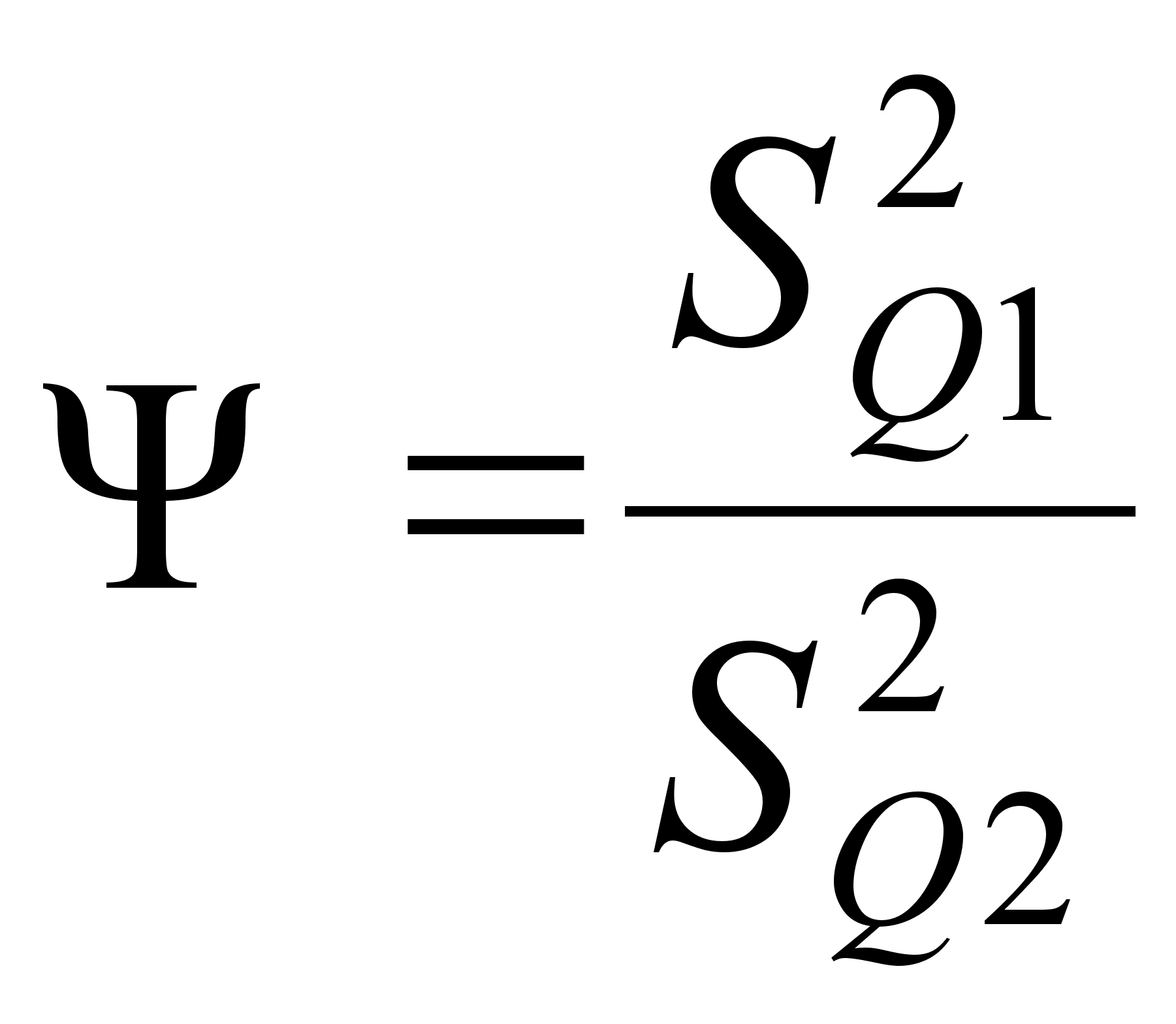 (23)
(23)
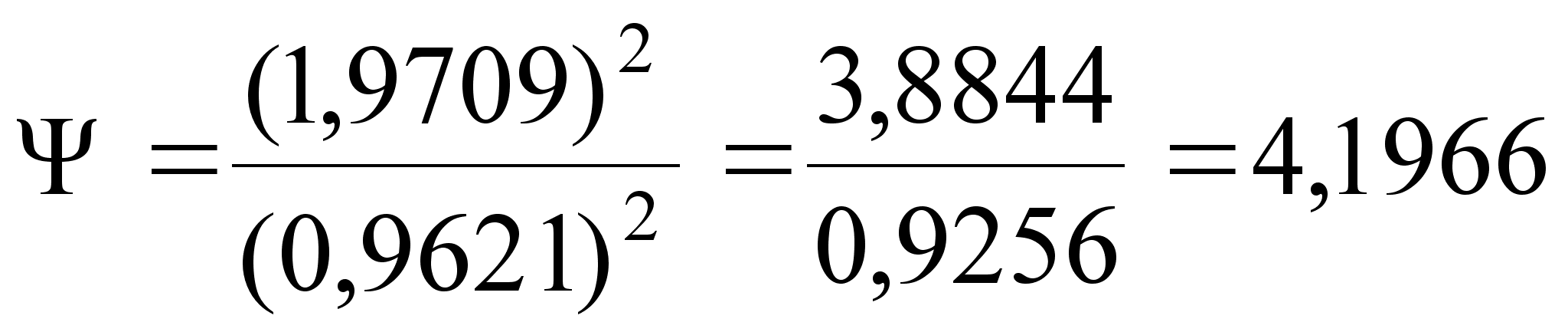 > 1
> 1
Из таблицы находим значение аргумента интегральной функции распределения Фишера Ψ0; Ψ0=1,96 при P=0,95.
Сравниваем Ψ и Ψ0: Ψ > Ψ0, следовательно, серии с доверительной вероятностью P = 0,95 считаем рассеянными.
4. Обрабатываем совместно результаты измерения обеих серий с учетом весовых коэффициентов:
– определяем
оценки результата
измерения![]() и среднеквадратического
отклонения
S
и среднеквадратического
отклонения
S
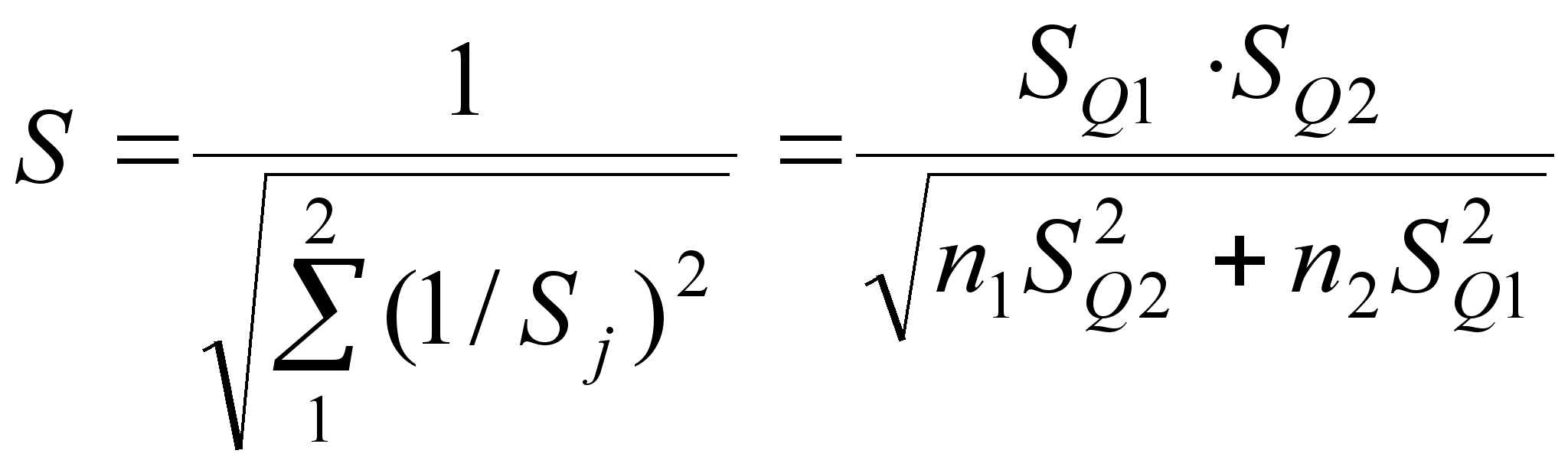 (24)
(24)
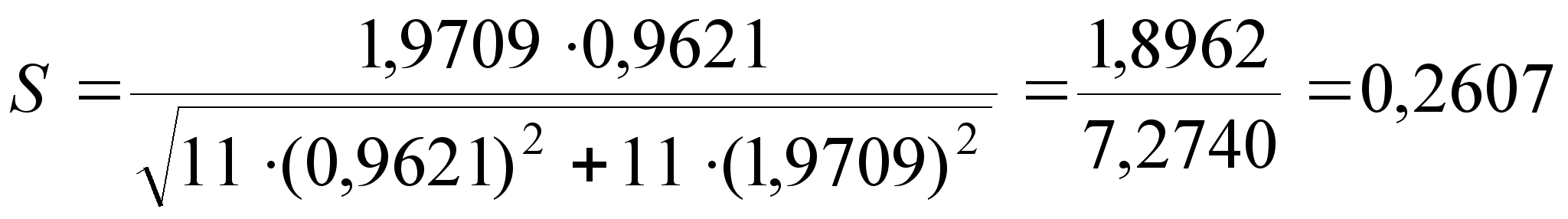
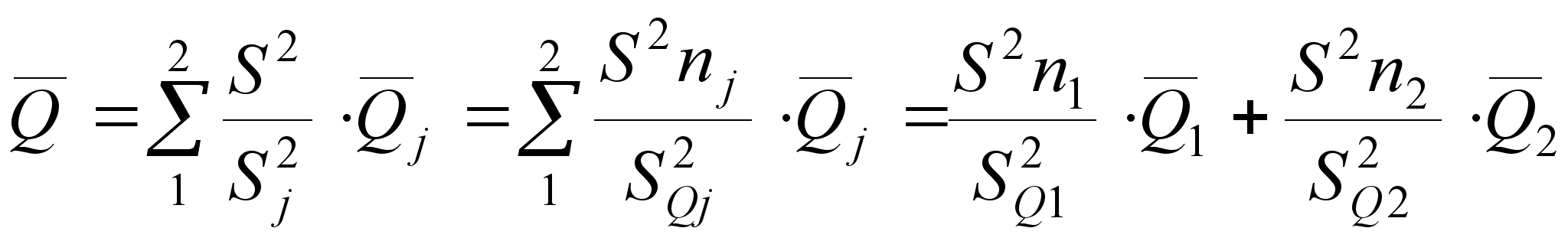 (25)
(25)
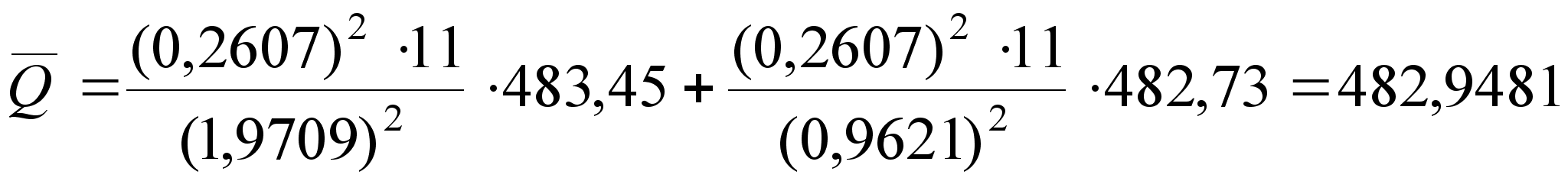
– задавшись доверительной вероятностью P = 0,95, определяем по таблице t = 1,96. Определяем доверительный интервал.
![]()
![]()
![]()
4. Функциональные преобразования результатов измерений (косвенные измерения)
Условие. При многократных измерениях независимых величин X и Y получено по 12 (n) результатов измерений. Эти результаты после внесения поправок представлены в таблице 8. Определить результат вычисления Z = f (X,Y).
Исходные данные:
Таблица 8
|
Функция Z=f(X,Y) |
№ изме-рения | Значения величин | |||
|
X – масса |
Y – радиус сферы |
||||
| мкг | кг | мкм | м | ||
|
плотность материала Z=3X/4πY3 |
1 | 482 |
4,82·10-7 |
483 |
4,83·10-4 |
| 2 | 485 |
4,85·10-7 |
483 |
4,83·10-4 |
|
| 3 | 486 |
4,86·10-7 |
483 |
4,83·10-4 |
|
| 4 | 486 |
4,86·10-7 |
483 |
4,83·10-4 |
|
| 5 | 483 |
4,83·10-7 |
484 |
4,84·10-4 |
|
| 6 | 483 |
4,83·10-7 |
484 |
4,84·10-4 |
|
| 7 | 483 |
4,83·10-7 |
483 |
4,83·10-4 |
|
| 8 | 483 |
4,83·10-7 |
482 |
4,82·10-4 |
|
| 9 | 481 |
4,81·10-7 |
481 |
4,81·10-4 |
|
| 10 | 480 |
4,80·10-7 |
481 |
4,81·10-4 |
|
| 11 | 492 |
4,92·10-7 |
483 |
4,83·10-4 |
|
| 12 | 486 |
4,86·10-7 |
495 |
4,95·10-4 |
|
Расчет.
1. Обрабатываем экспериментальные данные по алгоритму, изложенному в п.п. 1–3 задания 2, при этом:
– определяем
оценки результатов
измерений
![]() ,
,
![]() и среднеквадратических
отклонений
и среднеквадратических
отклонений
![]() и
и
![]() ;
;
– обнаруживаем и исключаем ошибки;
– проверяем гипотезу о нормальности распределения оставшихся результатов измерений.
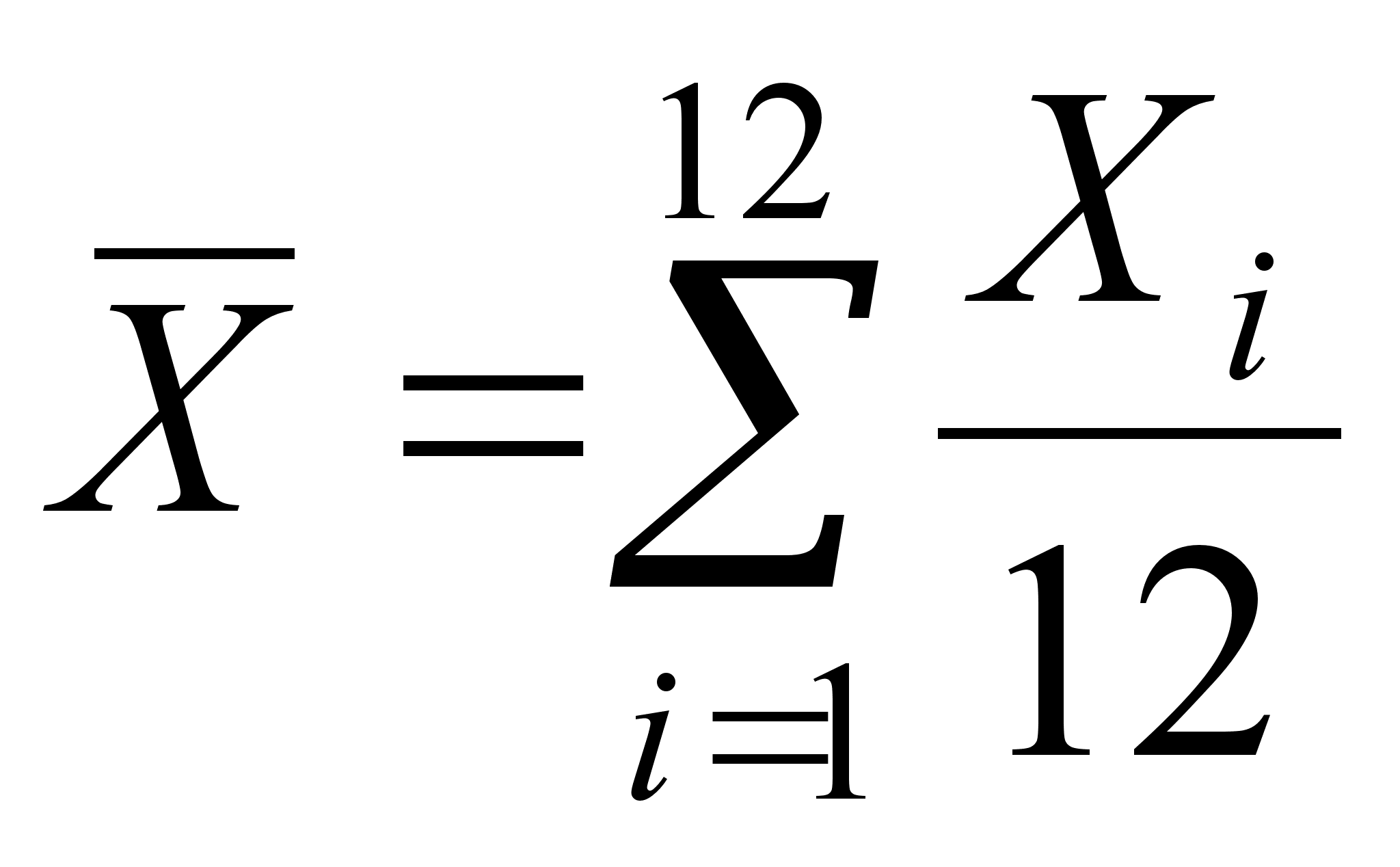 ;
; 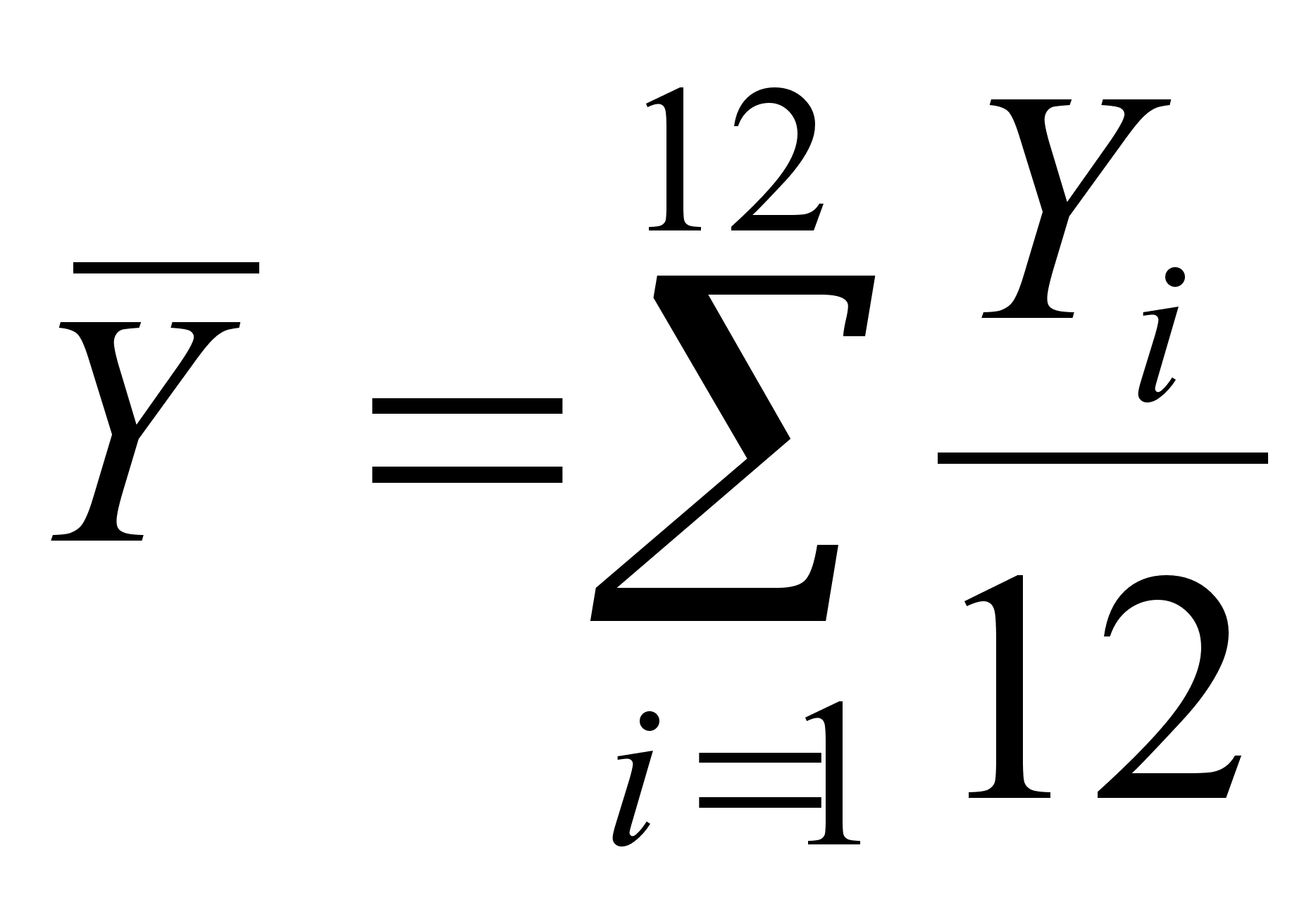 (25)
(25)
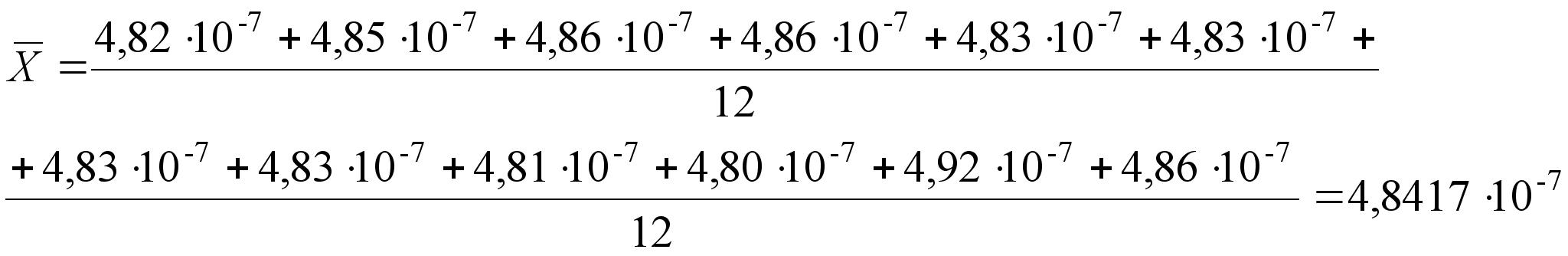
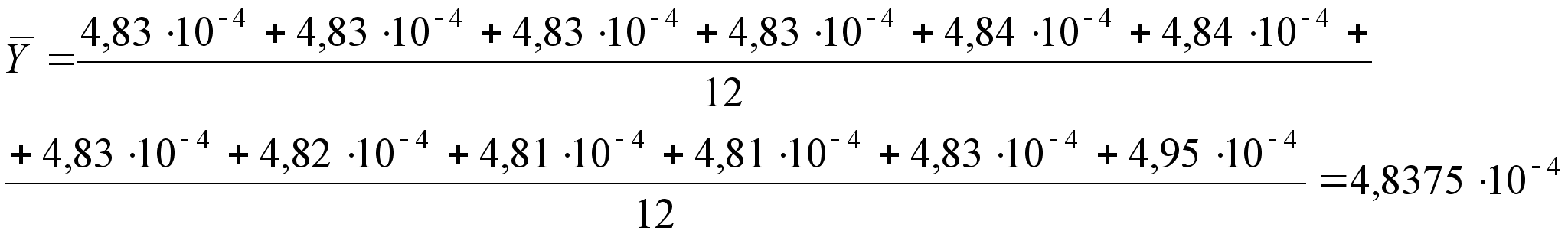
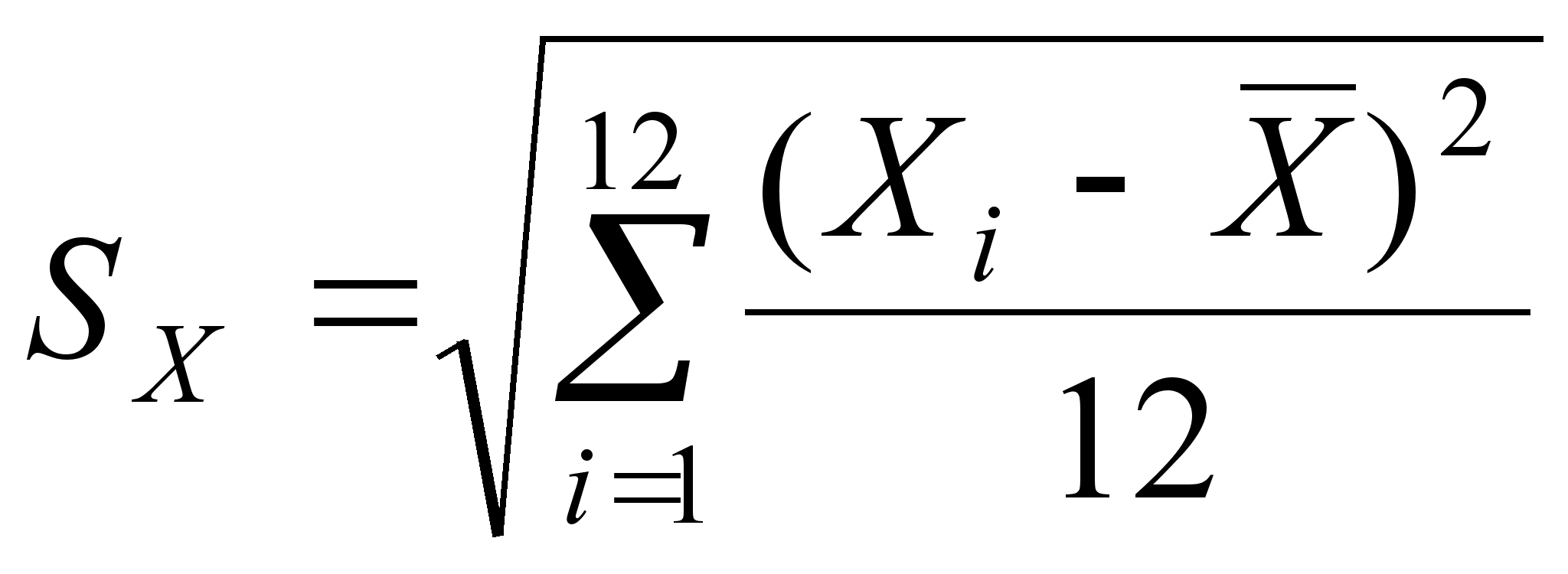 ;
; 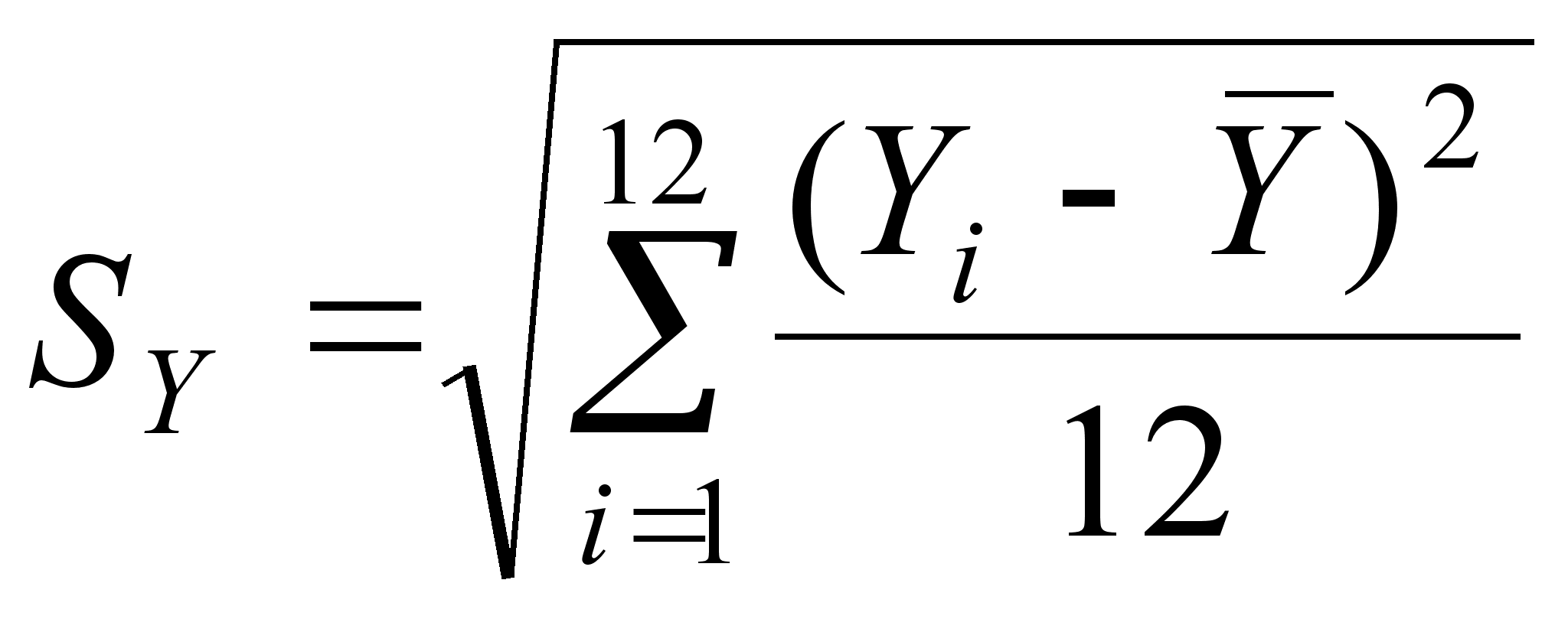 (26)
(26)
Таблица 9
|
Значения X |
Значения Y |
||||||
| № из-мерения |
Результат измере-ния (Xi) |
|
|
№ из-мерения |
Результат измере-ния (Yi) |
|
|
| 1 |
4,82·10-7 |
-2,1667·10-9 |
4,6944·10-18 |
1 |
4,83·10-4 |
-7,5·10-7 |
5,625·10-13 |
| 2 |
4,85·10-7 |
8,3333·10-10 |
6,9444·10-19 |
2 |
4,83·10-4 |
-7,5·10-7 |
5,625·10-13 |
| 3 |
4,86·10-7 |
1,8333·10-9 |
3,3611·10-18 |
3 |
4,83·10-4 |
-7,5·10-7 |
5,625·10-13 |
| 4 |
4,86·10-7 |
1,8333·10-9 |
3,3611·10-18 |
4 |
4,83·10-4 |
-7,5·10-7 |
5,625·10-13 |
| 5 |
4,83·10-7 |
-1,1667·10-9 |
1,3611·10-18 |
5 |
4,84·10-4 |
2,5·10-7 |
6,25·10-14 |
| 6 |
4,83·10-7 |
-1,1667·10-9 |
1,3611·10-18 |
6 |
4,84·10-4 |
2,5·10-7 |
6,25·10-14 |
| 7 |
4,83·10-7 |
-1,1667·10-9 |
1,3611·10-18 |
7 |
4,83·10-4 |
-7,5·10-7 |
5,625·10-13 |
| 8 |
4,83·10-7 |
-1,1667·10-9 |
1,3611·10-18 |
8 |
4,82·10-4 |
-1,75·10-6 |
3,0625·10-12 |
| 9 |
4,81·10-7 |
-3,1667·10-9 |
1,0028·10-17 |
9 |
4,81·10-4 |
-2,75·10-6 |
7,5625·10-12 |
| 10 |
4,80·10-7 |
-4,1667·10-9 |
1,7361·10-17 |
10 |
4,81·10-4 |
-2,75·10-6 |
7,5625·10-12 |
| 11 |
4,92·10-7 |
7,8333·10-9 |
6,1361·10-17 |
11 |
4,83·10-4 |
-7,5·10-7 |
5,625·10-13 |
| 12 |
4,86·10-7 |
1,8333·10-9 |
3,3611·10-18 |
12 |
4,95·10-4 |
1,125·10-5 |
1,2656·10-10 |
|
Σ |
0 |
1,0967·10-16 |
Σ |
0 |
1,4825·10-10 |
||
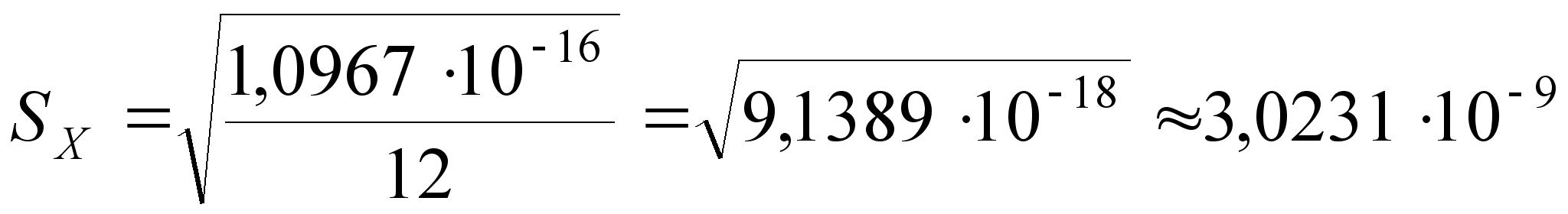 ;
;
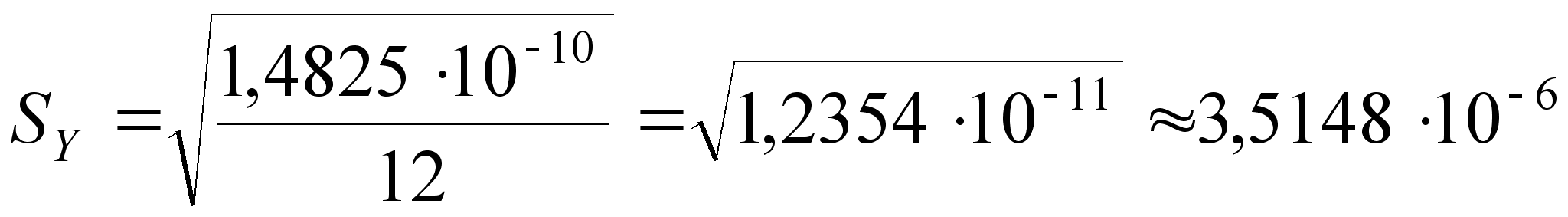 ;
;
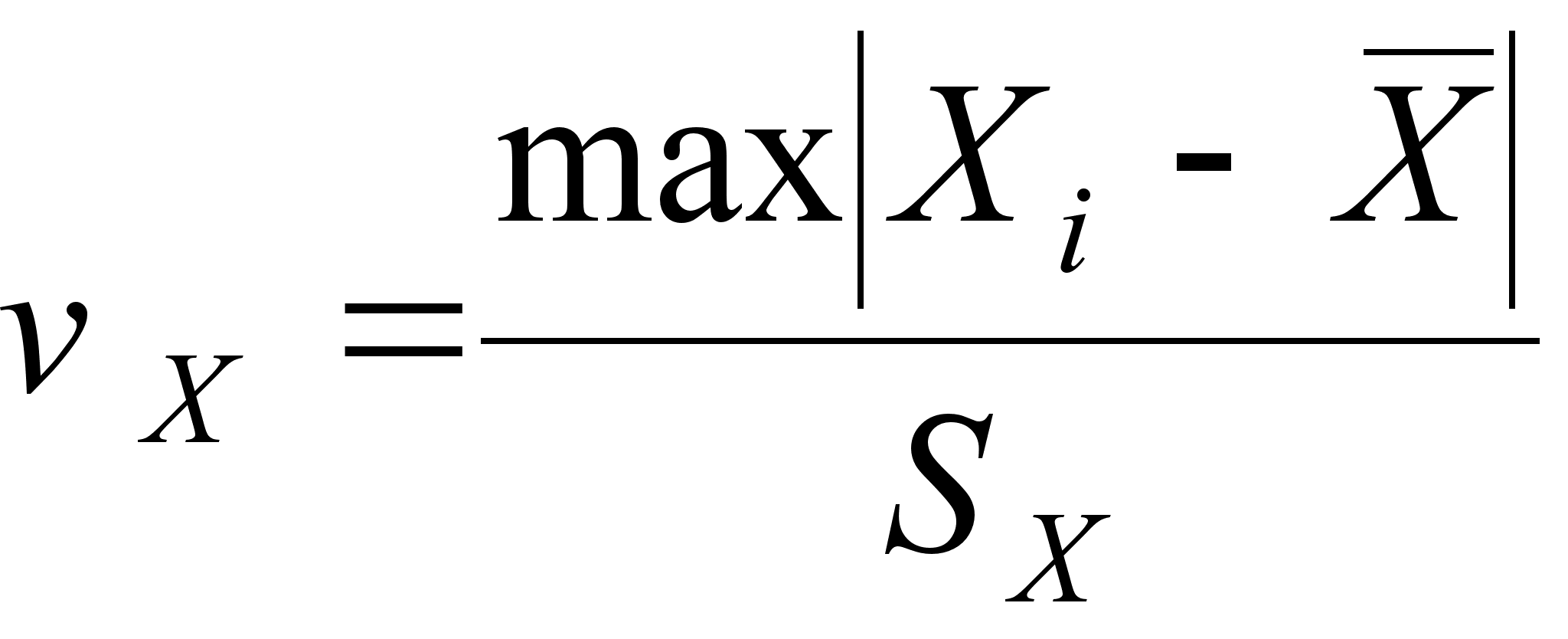 ;
; 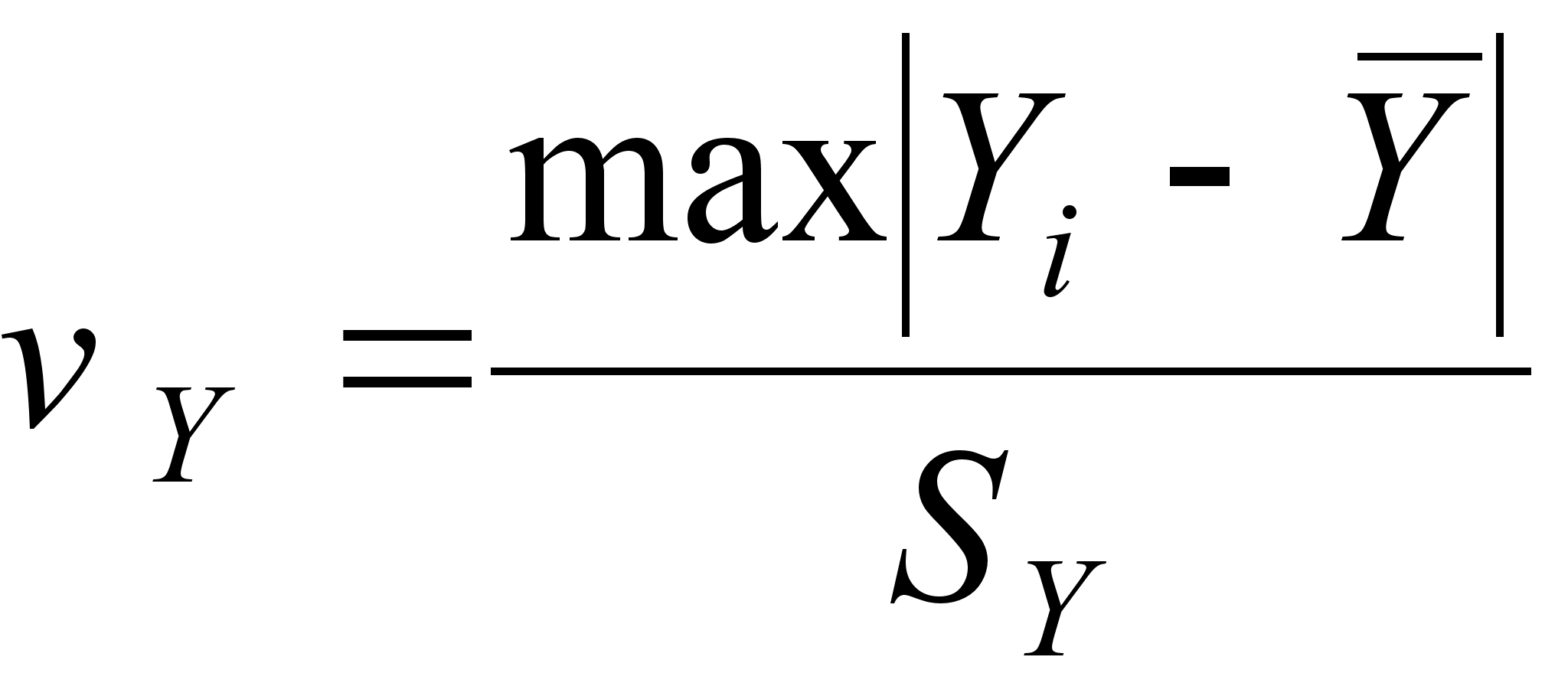 (27)
(27)
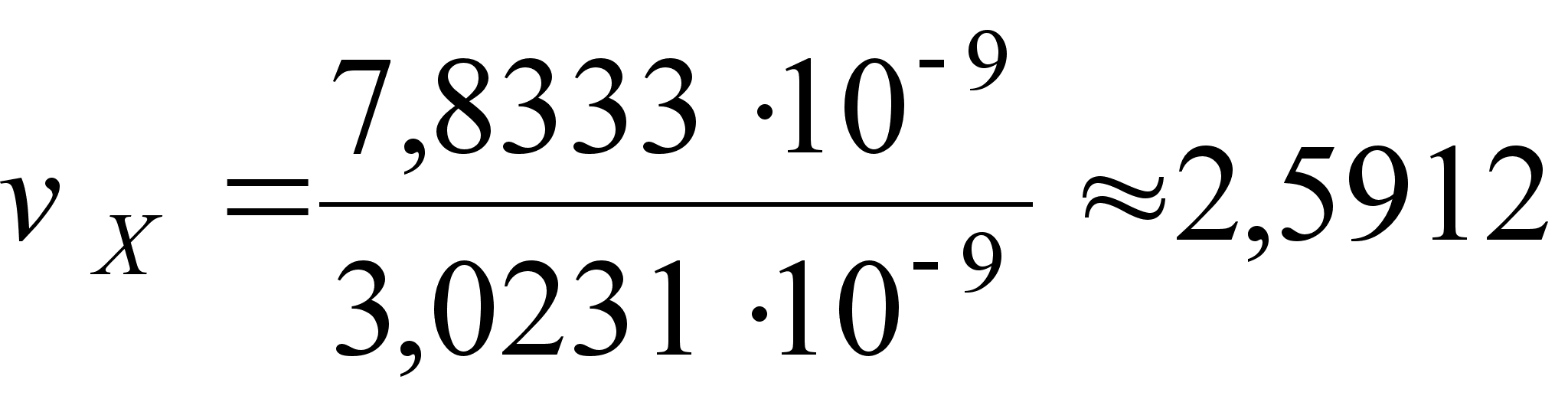 ;
;
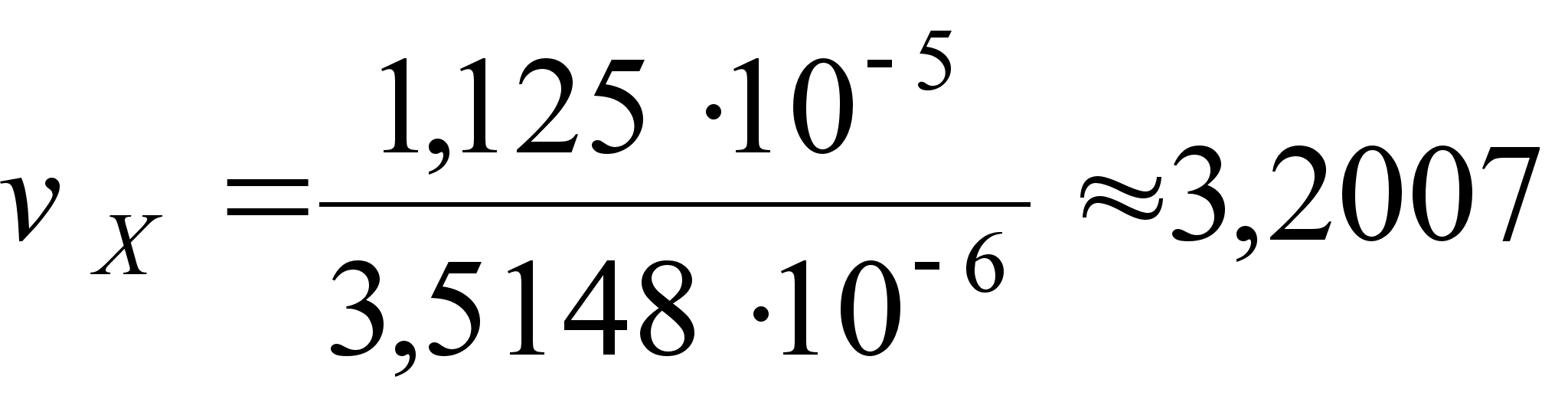 ;
;
![]() при n
= 12;
при n
= 12;
– сравниваем
![]() и
и
![]() с
с
![]() :
:
![]() и
и
![]() .
Результаты
измерения X11
и Y12
являются ошибочными,
они должны быть
отброшены.
.
Результаты
измерения X11
и Y12
являются ошибочными,
они должны быть
отброшены.
Повторяем вычисления, при этом отбрасываем измерения X11 и Y12:
Таблица 10
|
Значения X |
Значения Y |
||||||
| № из-мерения |
Результат измере-ния (Xi) |
|
|
№ из-мерения |
Результат измере-ния (Yi) |
|
|
| 1 |
4,82·10-7 |
-1,4545·10-9 |
2,1157·10-18 |
1 |
4,83·10-4 |
2,7273·10-7 |
0,07438·10-14 |
| 2 |
4,85·10-7 |
1,5455·10-9 |
2,3884·10-18 |
2 |
4,83·10-4 |
2,7273·10-7 |
0,07438·10-14 |
| 3 |
4,86·10-7 |
2,5455·10-9 |
6,4793·10-18 |
3 |
4,83·10-4 |
2,7273·10-7 |
0,07438·10-14 |
| 4 |
4,86·10-7 |
2,5455·10-9 |
6,4793·10-18 |
4 |
4,83·10-4 |
2,7273·10-7 |
0,07438·10-14 |
| 5 |
4,83·10-7 |
-4,5455·10-10 |
2,0661·10-19 |
5 |
4,84·10-4 |
1,2727·10-6 |
1,6198·10-12 |
| 6 |
4,83·10-7 |
-4,5455·10-10 |
2,0661·10-19 |
6 |
4,84·10-4 |
1,2727·10-6 |
1,6198·10-12 |
| 7 |
4,83·10-7 |
-4,5455·10-10 |
2,0661·10-19 |
7 |
4,83·10-4 |
2,7273·10-7 |
0,07438·10-14 |
| 8 |
4,83·10-7 |
-4,5455·10-10 |
2,0661·10-19 |
8 |
4,82·10-4 |
-7,2727·10-7 |
5,2893·10-13 |
| 9 |
4,81·10-7 |
-2,4545·10-9 |
6,0248·10-18 |
9 |
4,81·10-4 |
-1,7273·10-6 |
2,9835·10-12 |
| 10 |
4,80·10-7 |
-3,4545·10-9 |
1,1934·10-17 |
10 |
4,81·10-4 |
-1,7273·10-6 |
2,9835·10-12 |
| 11 |
4,86·10-7 |
2,5455·10-9 |
6,4793·10-18 |
11 |
4,83·10-4 |
2,7273·10-7 |
0,07438·10-14 |
|
Σ |
0 |
4,2727·10-17 |
Σ |
0 |
1,0182·10-11 |
||
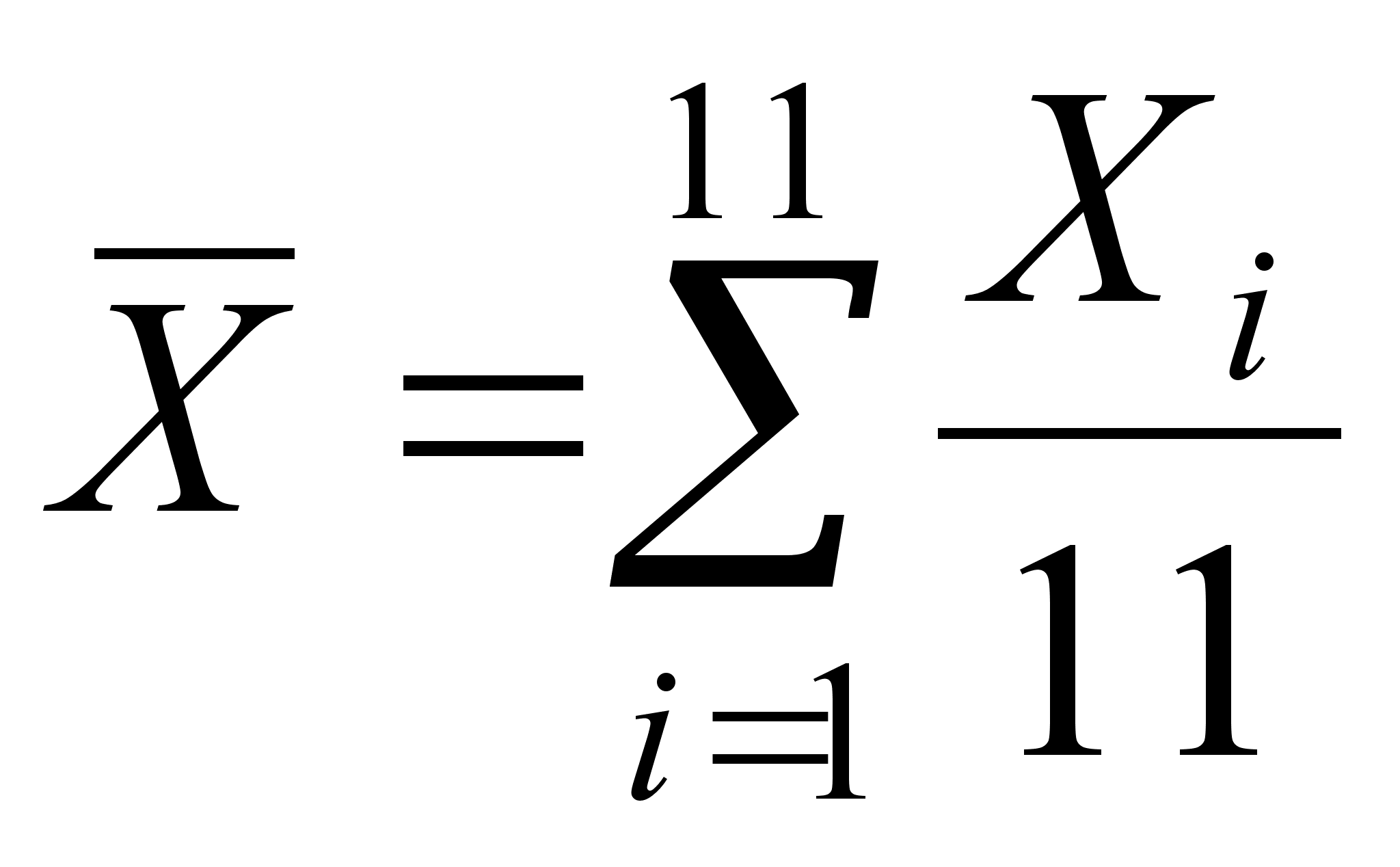
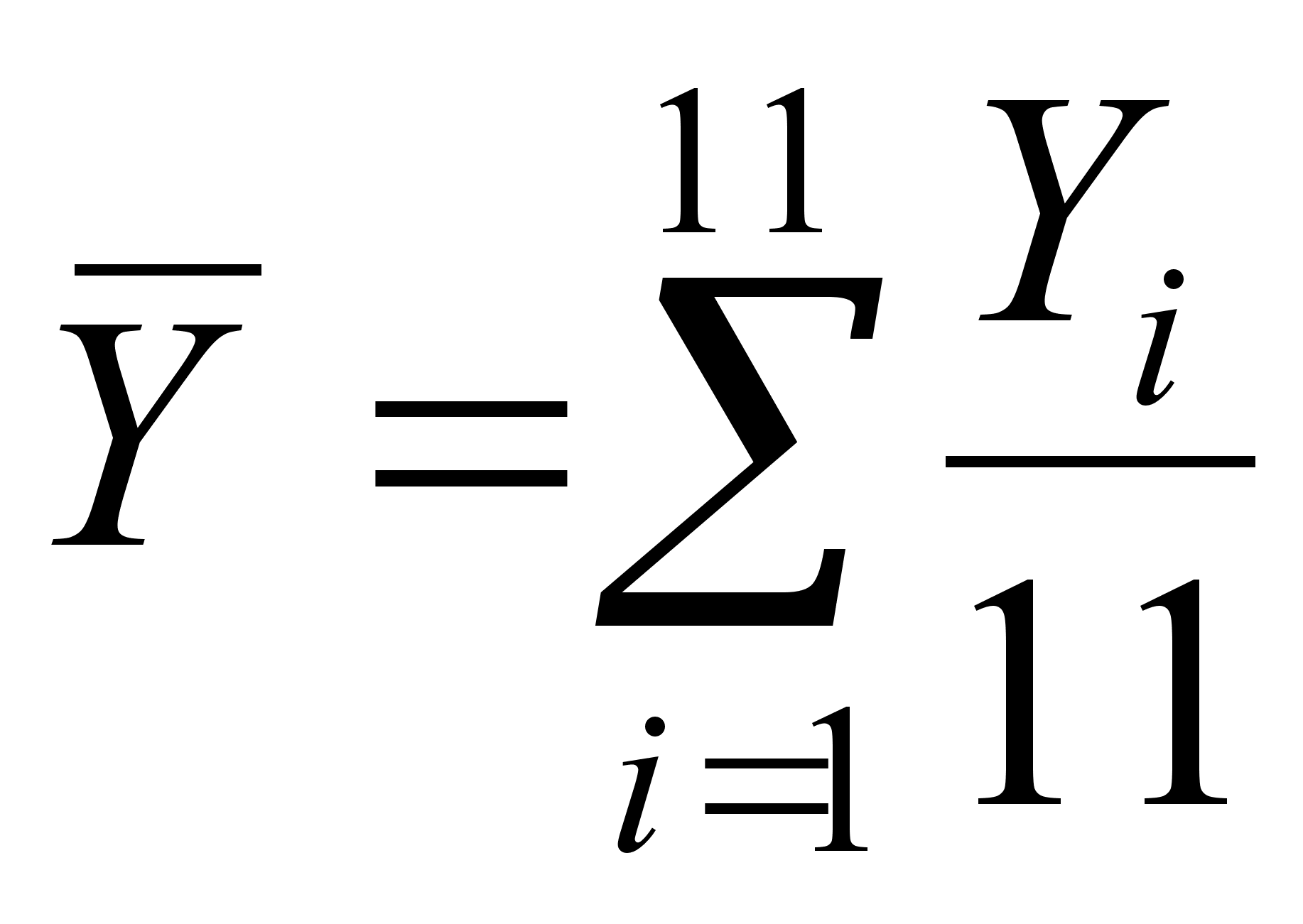 (28)
(28)
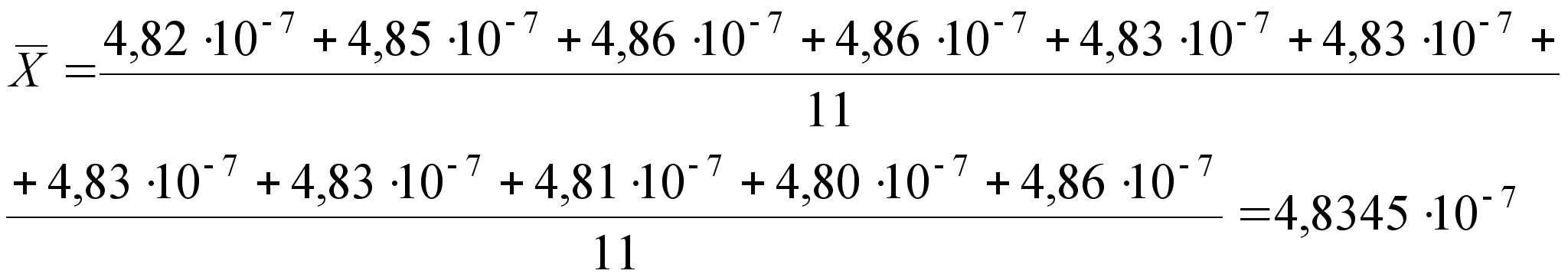
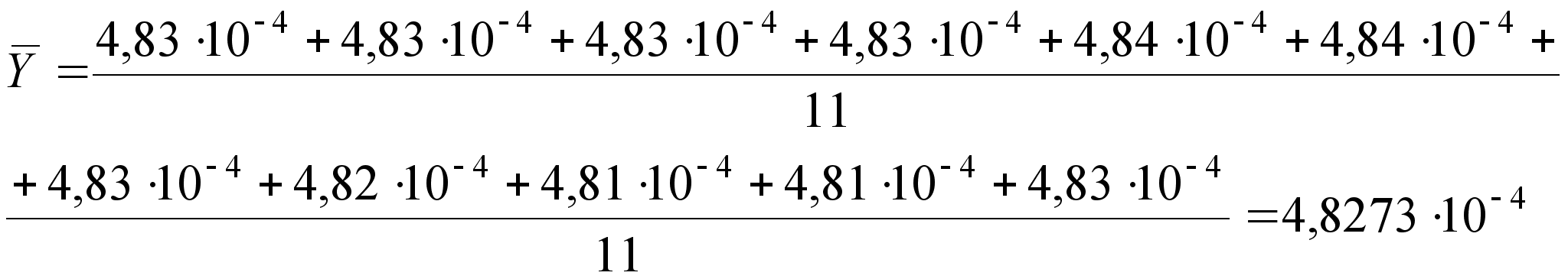
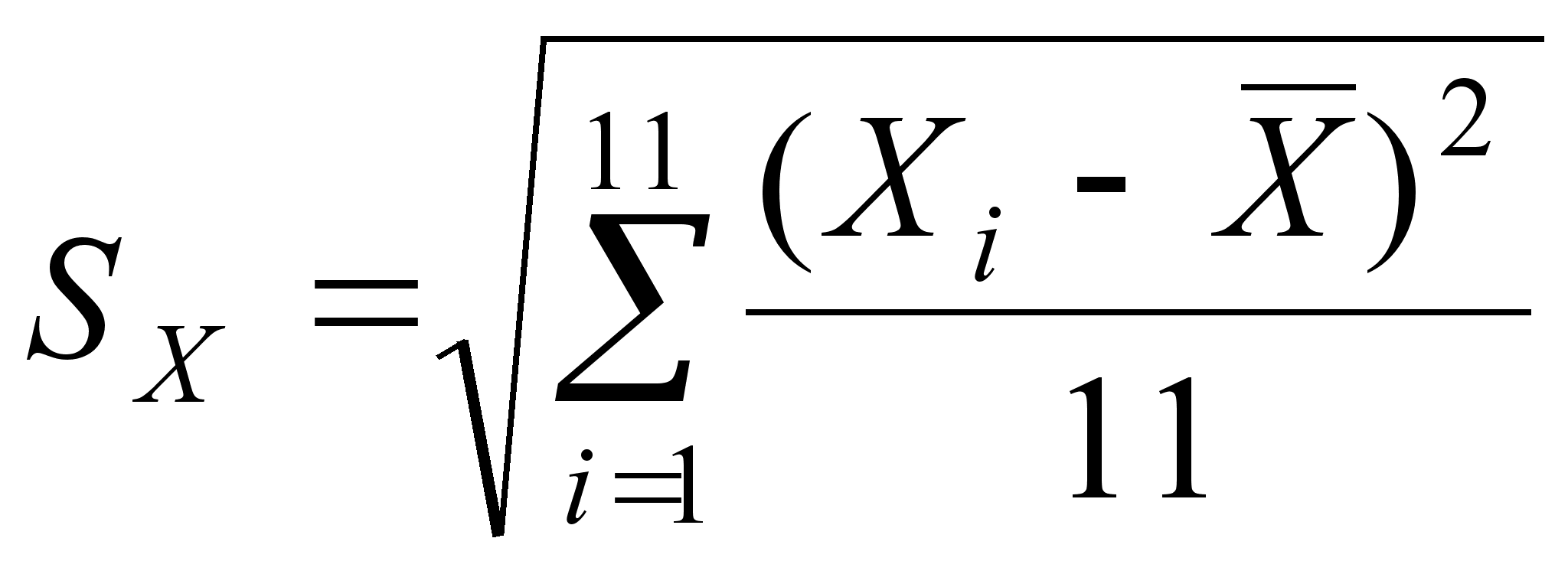 ;
;
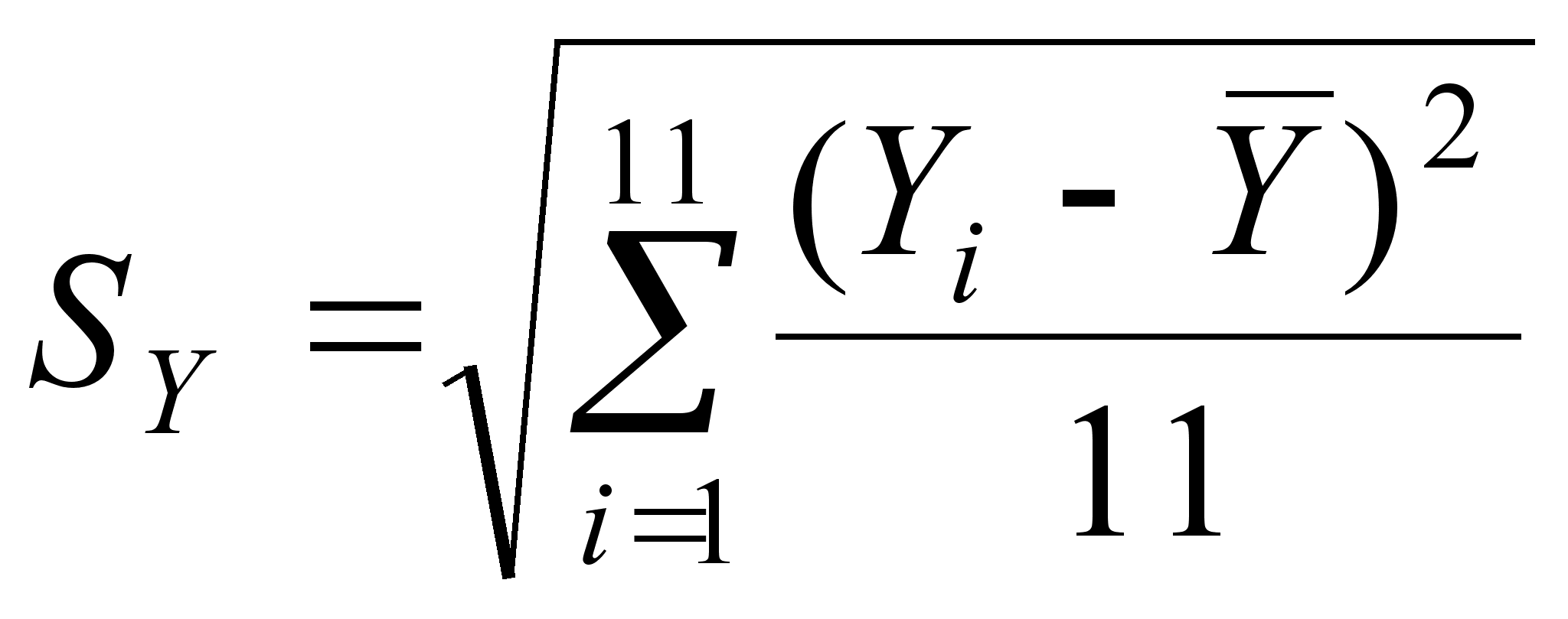 (29)
(29)
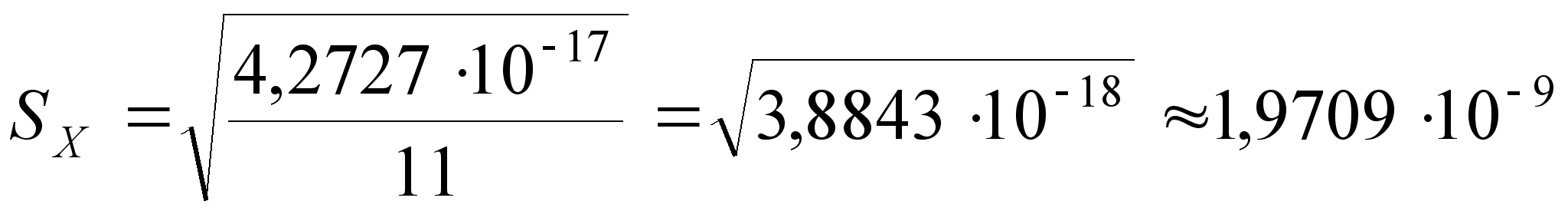 ;
;
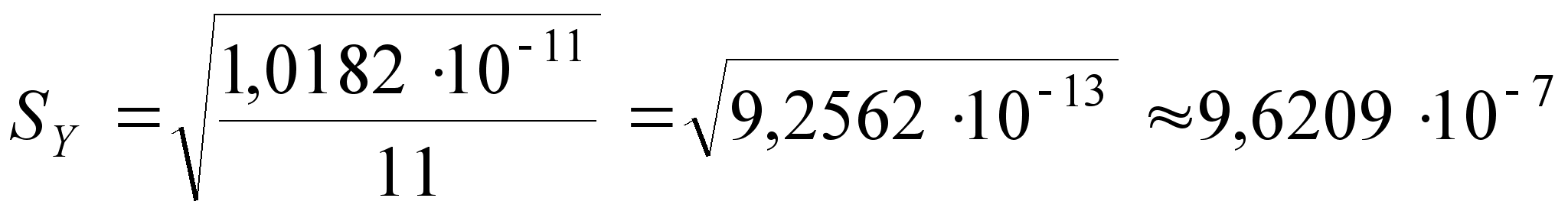
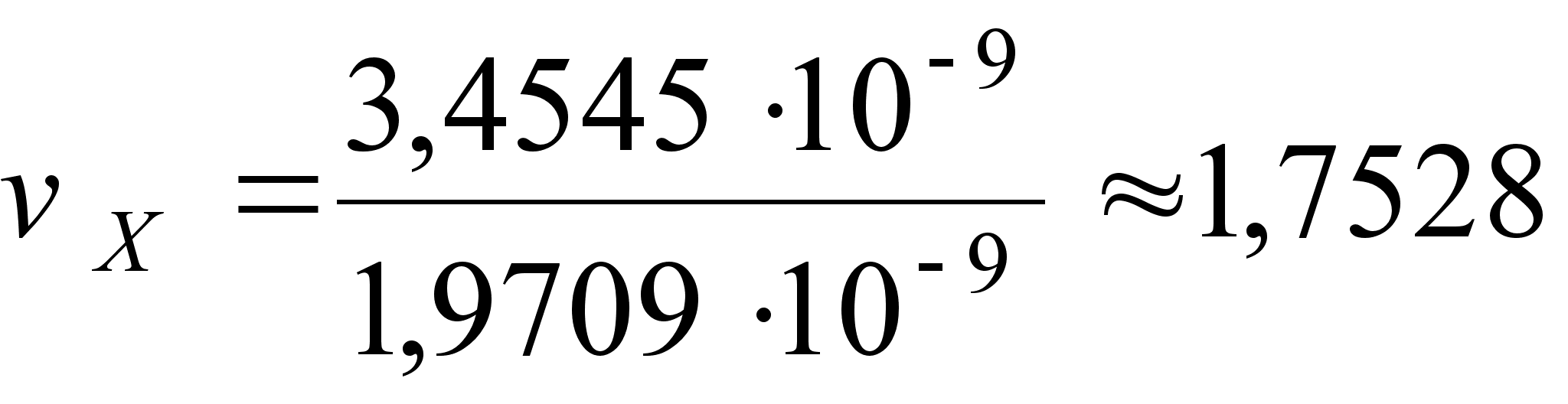 ;
;
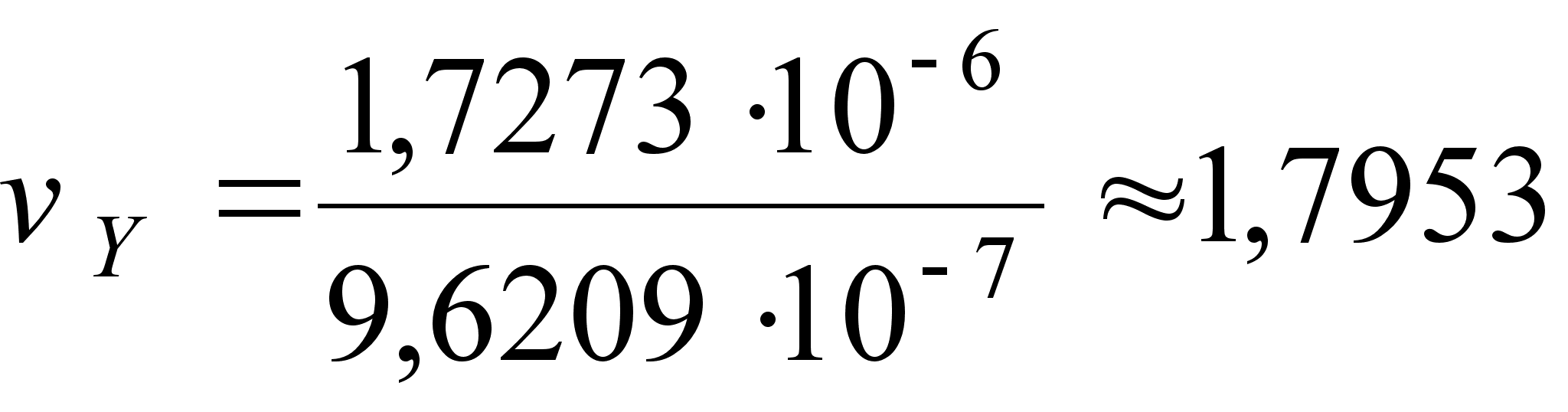 ;
;
![]() при n
= 11;
при n
= 11;
Сравниваем
![]() и
и
![]() с
с
![]() :
:
![]() и
и
![]() .
Результаты
измерений X10
и Y9
не являются
ошибочными
и окончательно
остается 11 измерений
для обоих видов
величин измерений,
т.е. n
= 11.
.
Результаты
измерений X10
и Y9
не являются
ошибочными
и окончательно
остается 11 измерений
для обоих видов
величин измерений,
т.е. n
= 11.
Так как
n
![]() .
.
2. Определяем оценку среднего значения функции
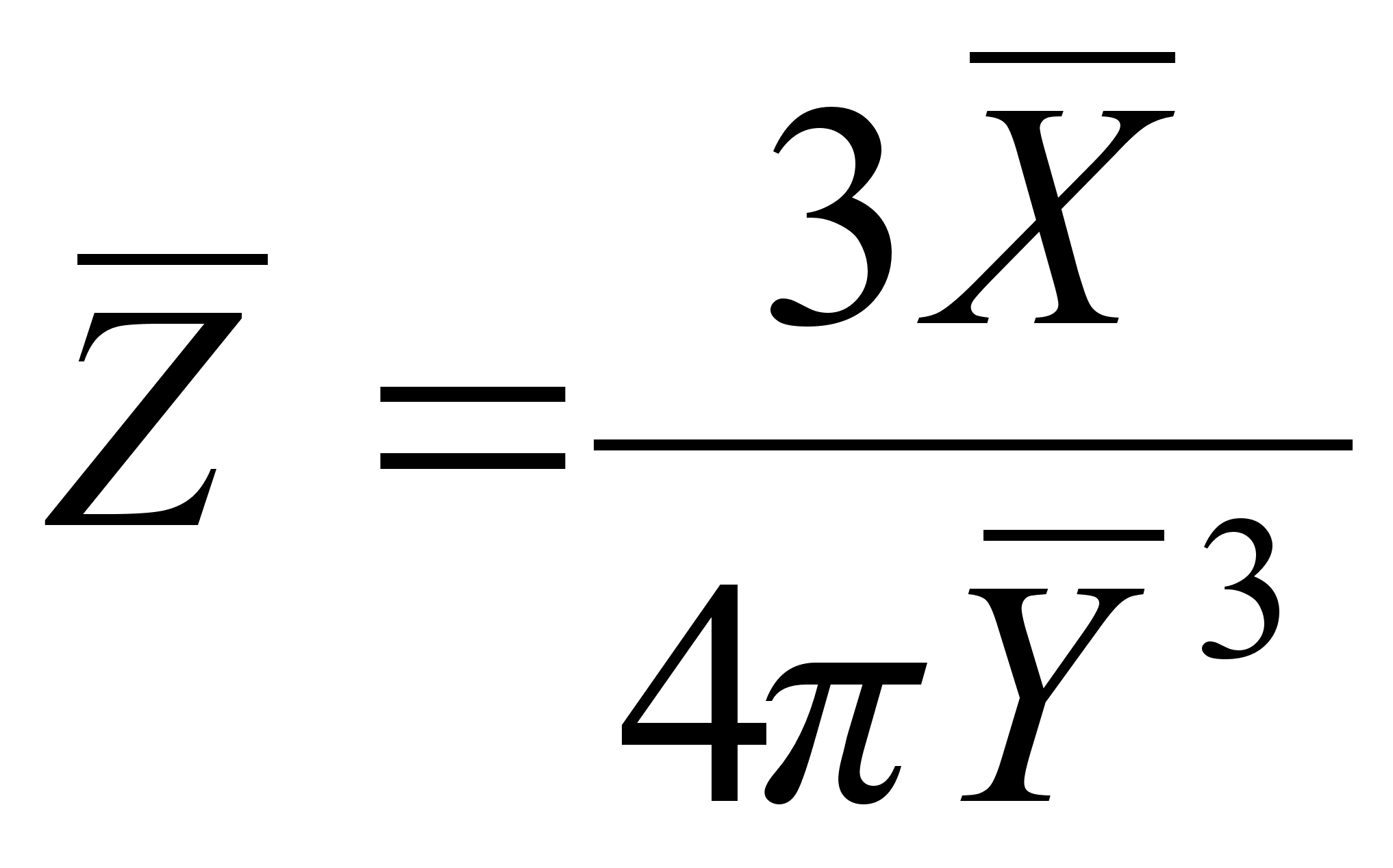 ; (30)
; (30)
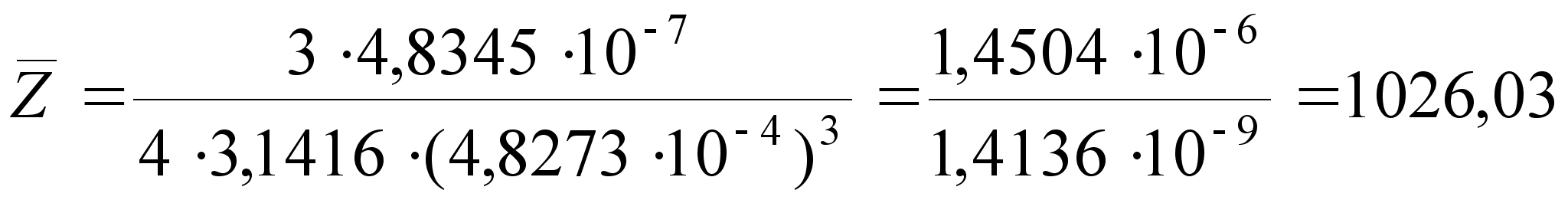
3. Находим частные производные первого и второго порядка для функции Z = f (X,Y) по X и Y.
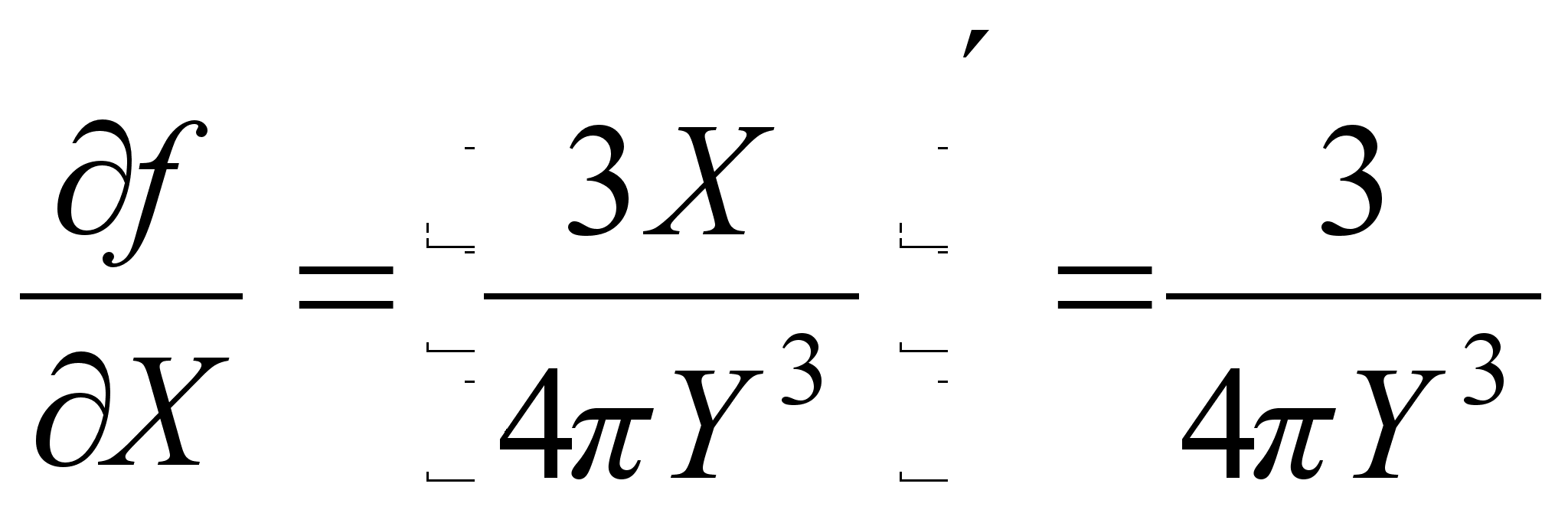 ;
;
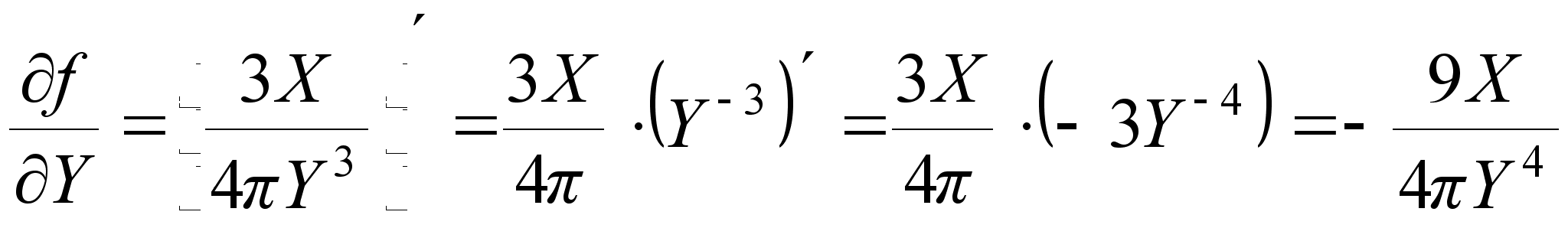 ;
;
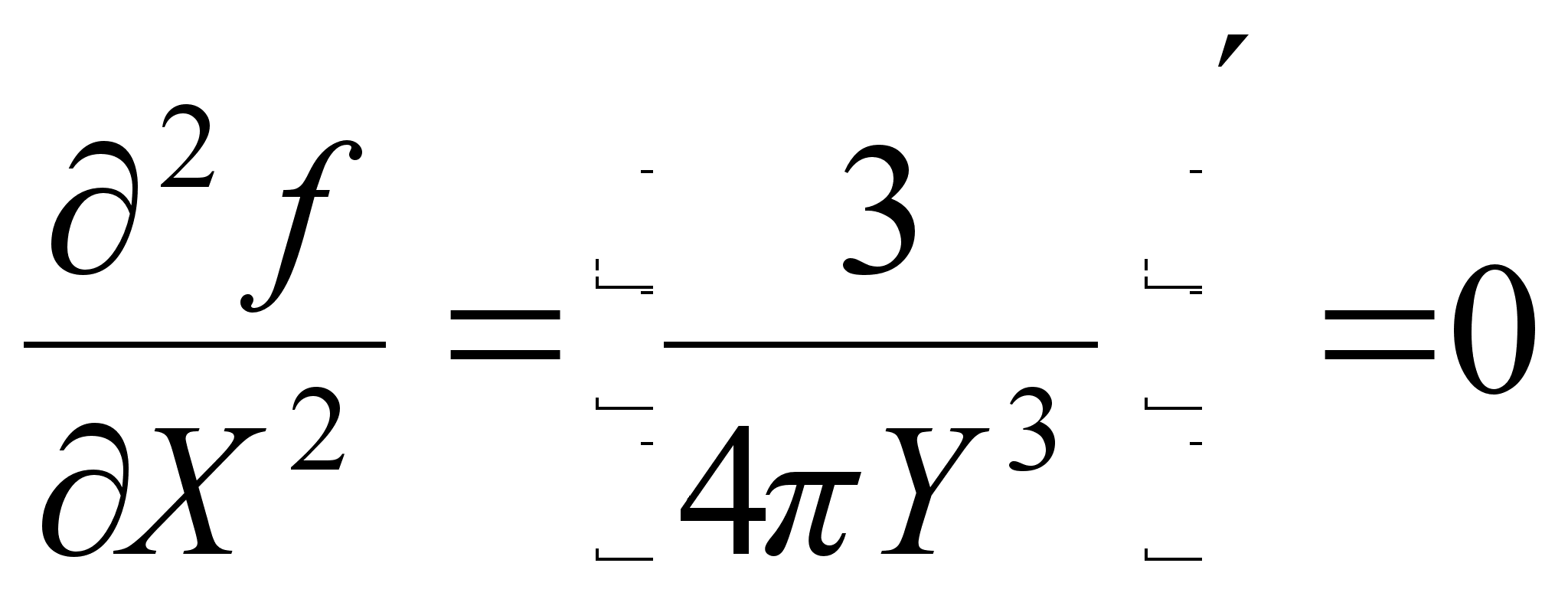 ;
;
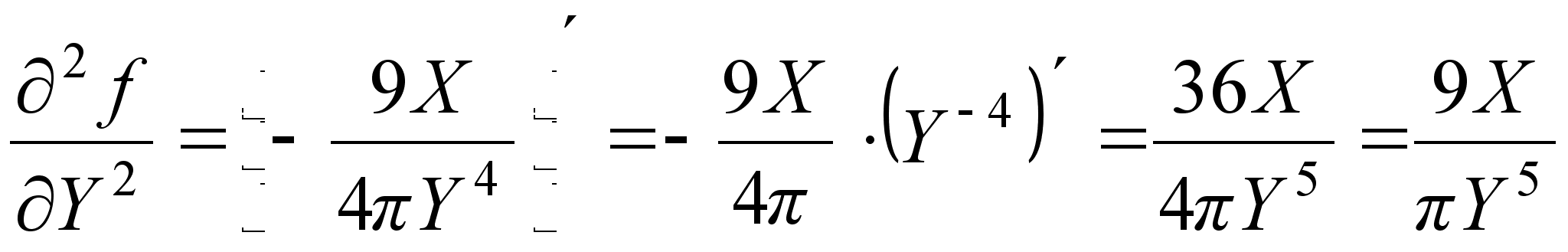 ;
;
Определяем поправку:
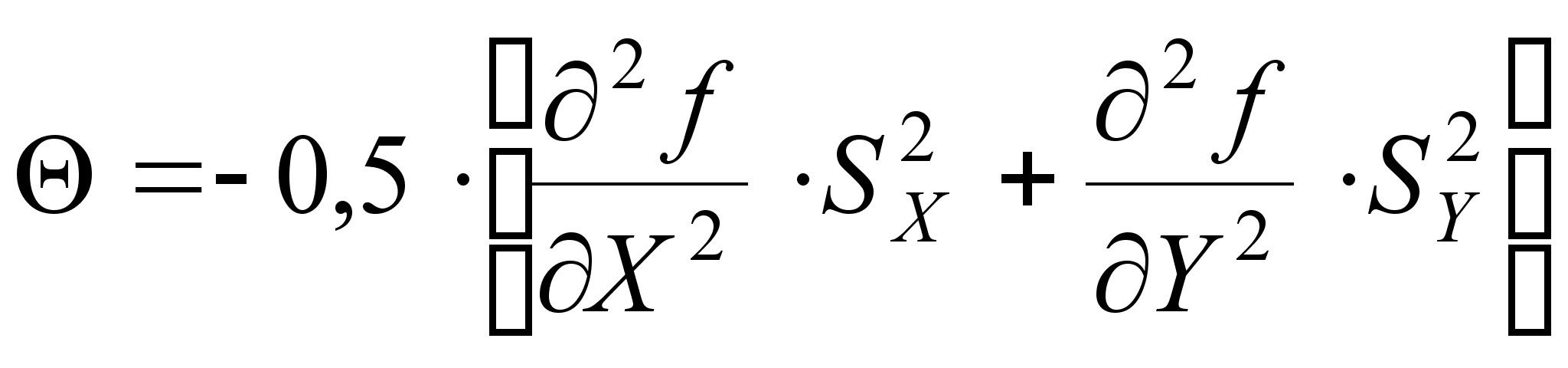 (31)
(31)
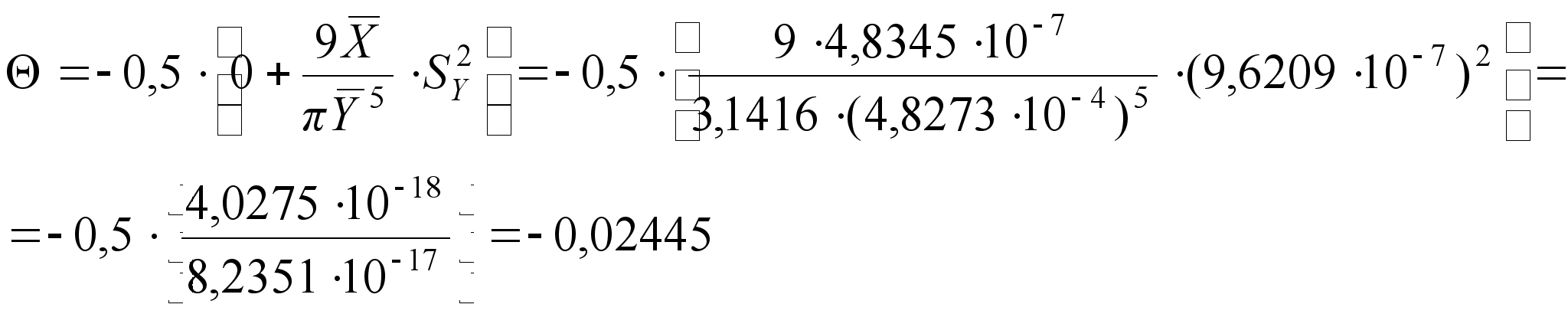
4. Определяем оценку стандартного отклонения функции
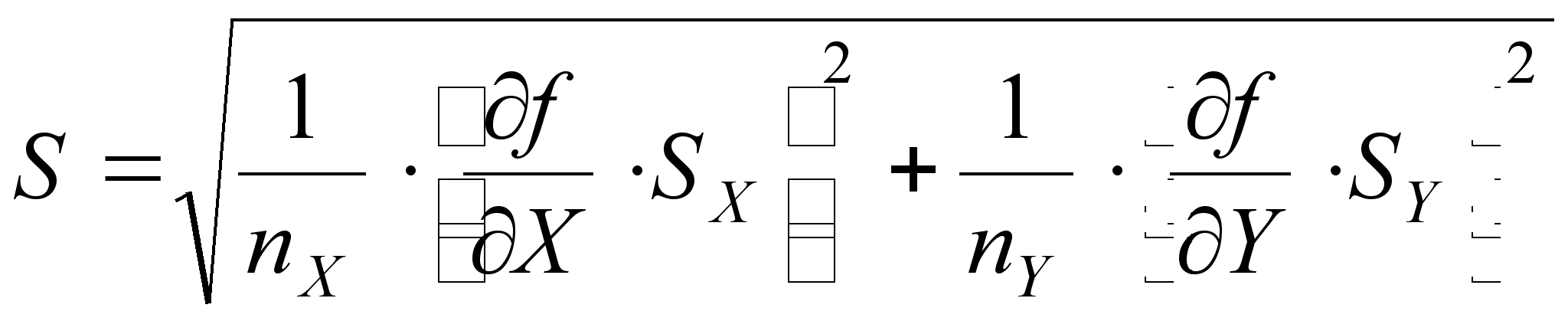 (32)
(32)
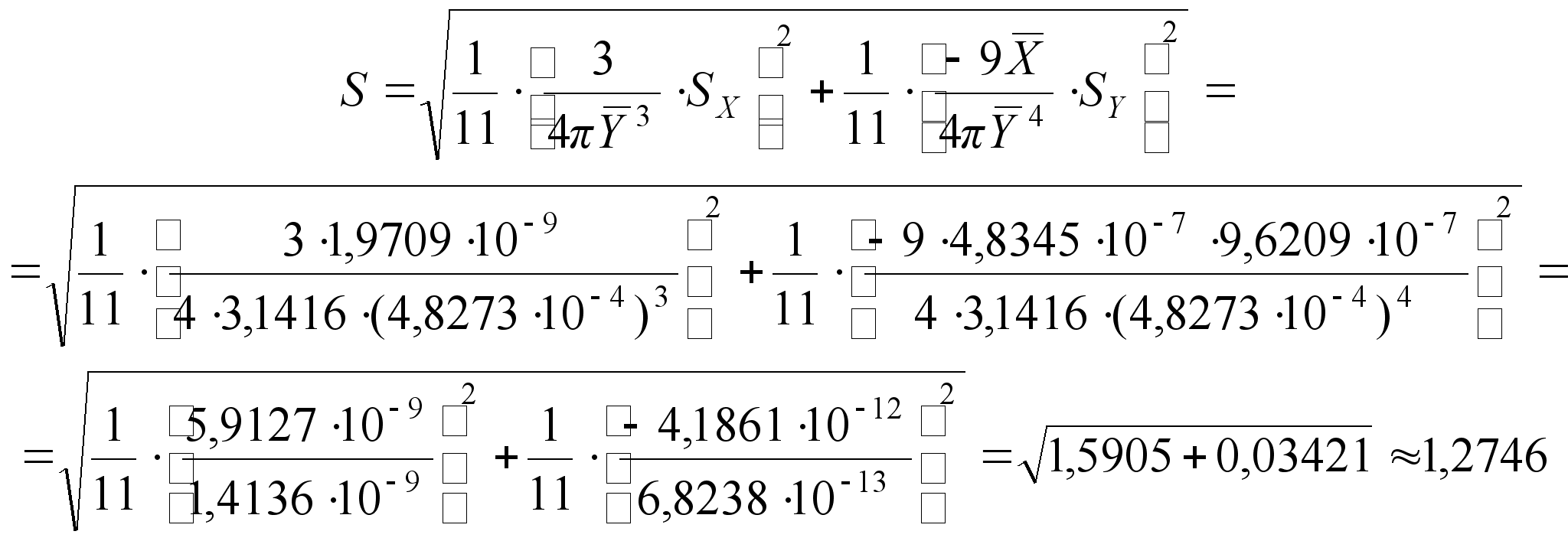
5. Находим число степеней свободы
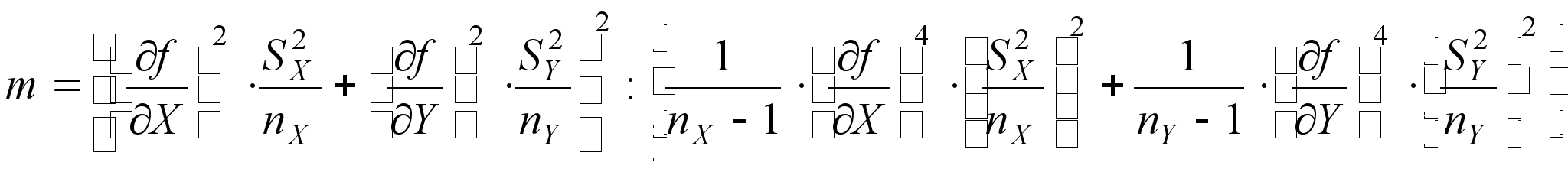 (33)
(33)
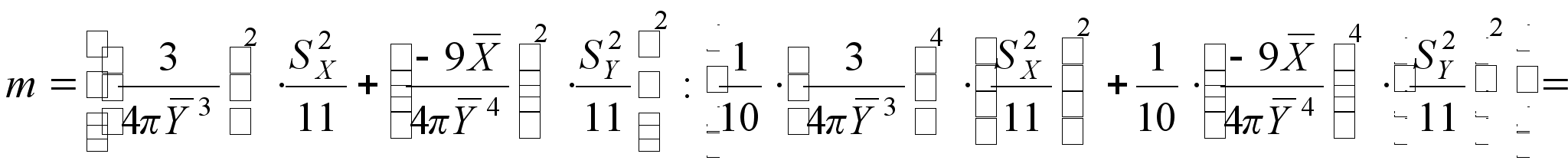
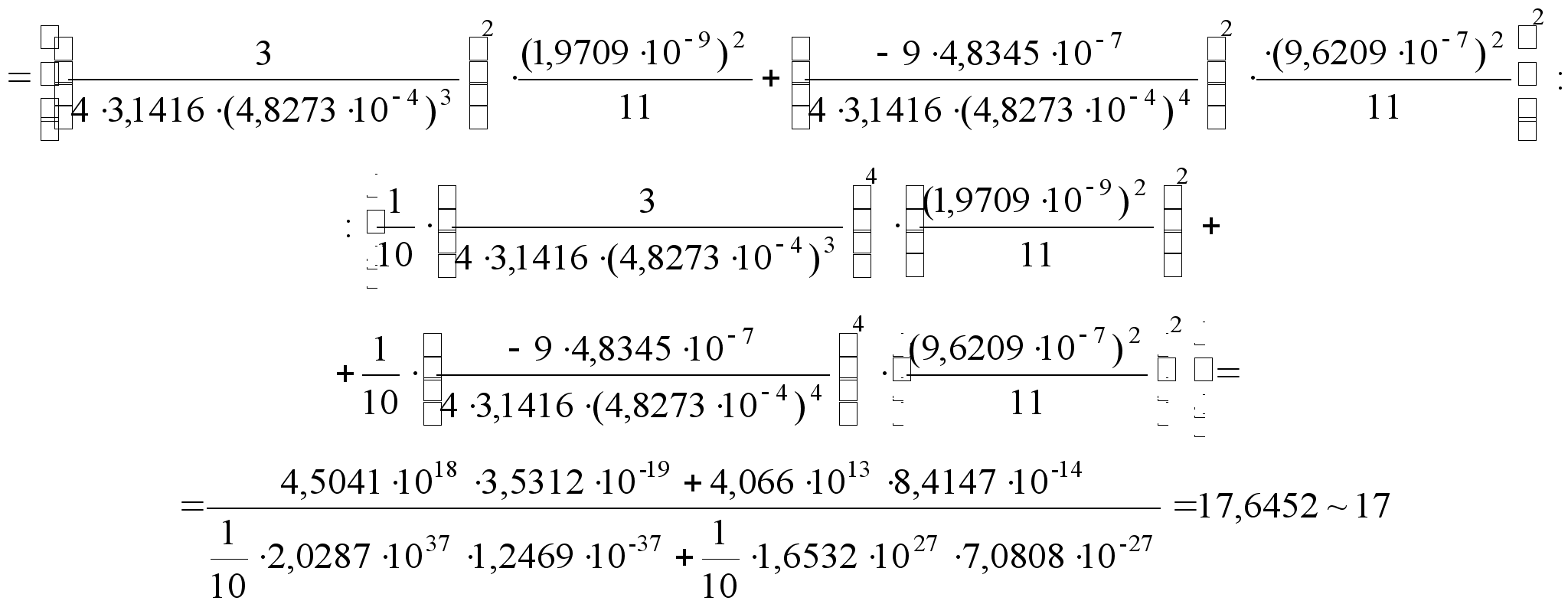
Определяем доверительный интервал для функции, для этого задаемся доверительной вероятностью P = 0,98 и из распределения Стьюдента находим t
n = m + 1 = 17 + 1 = 18
t = 2,57
![]() (34)
(34)
![]()
Значение функции будет находиться в промежутке:
![]()
![]()
5. Определение погрешностей результатов измерений методом математической статистики
Условие. В ходе измерений физической величины получены 100 результатов измерения, представленных в таблице 11. Исключить погрешности и определить достоверный результат измерения.
Исходные данные:
Таблица 11
| 20,05 | 20,24 | 20,17 | 20,16 | 20,08 | 20,22 | 20,19 |
| 20,01 | 20,28 | 20,15 | 20,17 | 20,25 | 20,23 | 20,20 |
| 20,04 | 20,26 | 20,16 | 20,18 | 20,23 | 20,21 | 20,10 |
| 20,30 | 20,28 | 20,17 | 20,19 | 20,06 | 20,07 | 20,18 |
| 20,34 | 20,29 | 20,30 | 20,20 | 20,13 | 20,11 | 20,17 |
| 20,35 | 20,30 | 20,27 | 20,10 | 20,05 | 20,13 | 20,06 |
| 20,25 | 20,25 | 20,26 | 20,15 | 20,10 | 20,10 | 20,15 |
| 20,30 | 20,20 | 20,28 | 20,11 | 20,15 | 20,20 | 20,20 |
| 20,29 | 20,24 | 20,25 | 20,14 | 20,10 | 20,19 | 20,19 |
| 20,25 | 20,21 | 20,20 | 20,07 | 20,14 | 20,08 | 20,17 |
| 20,27 | 20,23 | 20,25 | 20,13 | 20,13 | 20,18 | |
| 20,20 | 20,15 | 20,24 | 20,14 | 20,12 | 20,17 | |
| 20,25 | 20,20 | 20,21 | 20,10 | 20,06 | 20,16 | |
| 20,21 | 20,17 | 20,22 | 20,14 | 20,25 | 20,09 | |
| 20,21 | 20,18 | 20,15 | 20,08 | 20,24 | 20,15 |
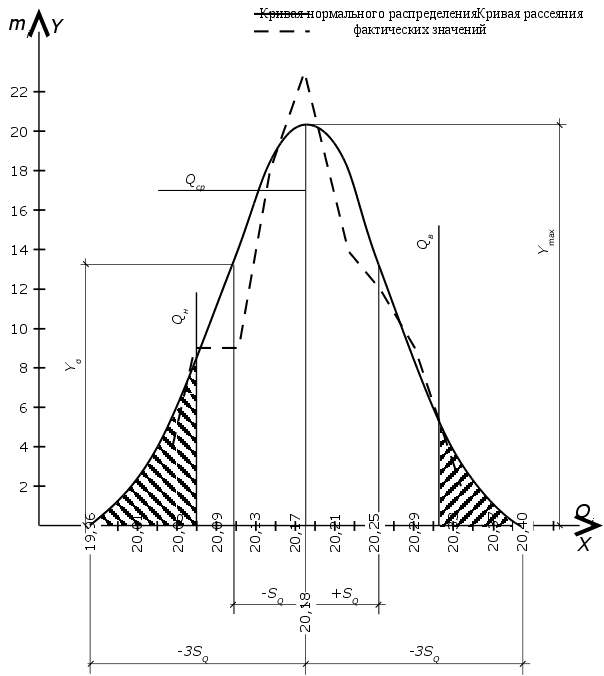
Расчет. Случайные погрешности, имеющие место при измерении, подчиняются закону нормального распределения, который графически изображается кривой Гаусса, имеющей симметричную форму с округленной вершиной и с каждой стороны по одной точке перегиба на некотором расстоянии от вершины.
При проведении исследования, чтобы составить графики и определить, на сколько полученная кривая рассеяния фактических результатов измерения приближается к теоретической кривой нормального распределения, обе кривые надо начертить совмещёнными в одинаковом масштабе. С этой целью рассчитаем данные, необходимые для построения кривой нормального распределения. Для сокращения расчетов и упрощения примерного построения кривой нормального распределения можно ограничиться определением только трех параметров: максимальной ординаты Ymax (при X = 0), ординаты для точек перегиба Yσ (при X = ±SQ) и величины поля рассеяния.
Результаты измерения Qi разбиваем на 9 групп через установленные интервалы с указанием абсолютной частоты (mi) появления результата измерения внутри каждого интервала. Данные располагаем для удобства расчетов в форме таблицы (таблица 12), заполняемой по мере проведения расчетов.
Величина интервала определяется по формуле:
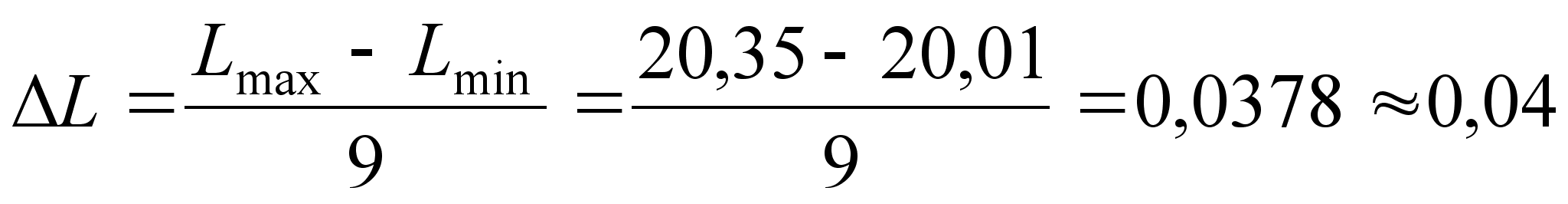 (35)
(35)
Таблица 12
| № группы | Границы интервала |
Qi |
mi |
Qi· mi |
|
|
|
| 1 | 20,01-20,05 | 20,0375 | 4 | 80,15 | -0,1470 | 21,5997 | 86,3989 |
| 2 | 20,06-20,09 | 20,0722 | 9 | 180,65 | -0,1122 | 12,5992 | 113,3929 |
| 3 | 20,10-20,12 | 20,1044 | 9 | 180,94 | -0,0800 | 6,4038 | 57,6345 |
| 4 | 20,13-20,16 | 20,1450 | 18 | 362,61 | -0,0395 | 1,5578 | 28,0396 |
| 5 | 20,17-20,20 | 20,1857 | 23 | 464,27 | 0,0012 | 0,0014 | 0,0322 |
| 6 | 20,21-20,24 | 20,2243 | 14 | 283,14 | 0,0398 | 1,5854 | 22,1959 |
| 7 | 20,25-20,27 | 20,2550 | 12 | 243,06 | 0,0705 | 4,9747 | 59,6965 |
| 8 | 20,28-20,31 | 20,2911 | 9 | 182,62 | 0,1066 | 11,3727 | 102,3540 |
| 9 | 20,32-20,35 | 20,3450 | 2 | 40,69 | 0,1605 | 25,7704 | 51,5408 |
|
Σ |
100 |
2018,13 |
0 |
521,2851 |
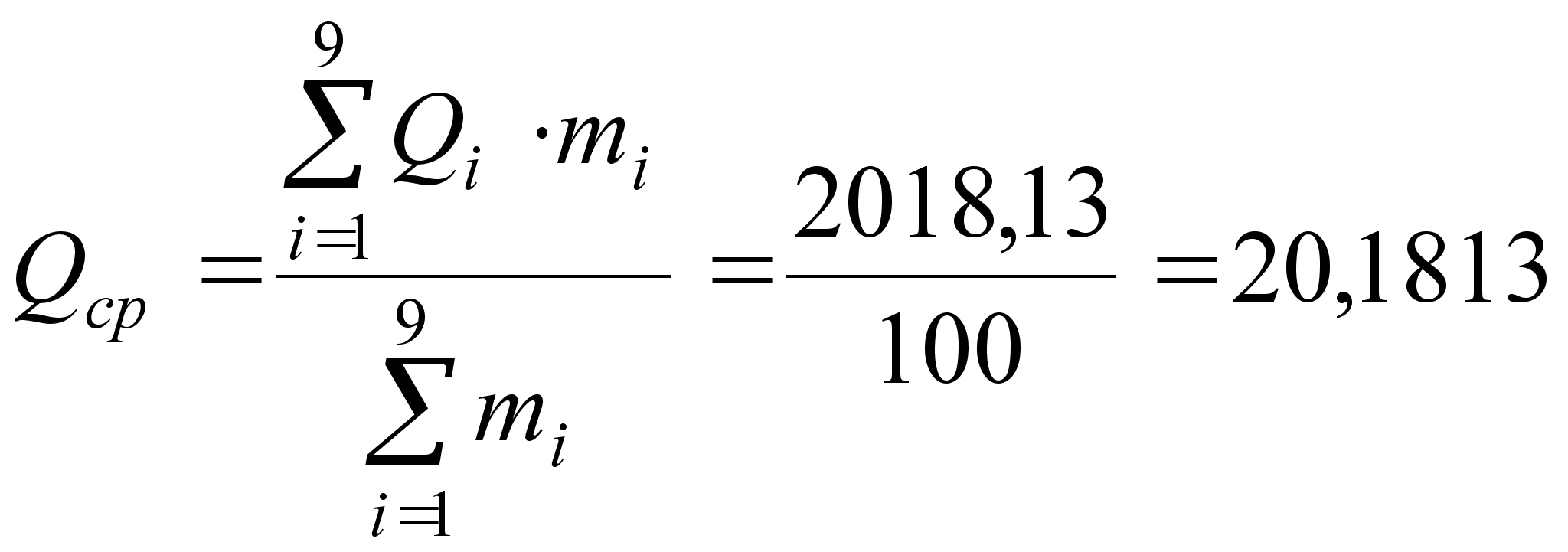 (36)
(36)
Определим среднеквадратическое отклонение:
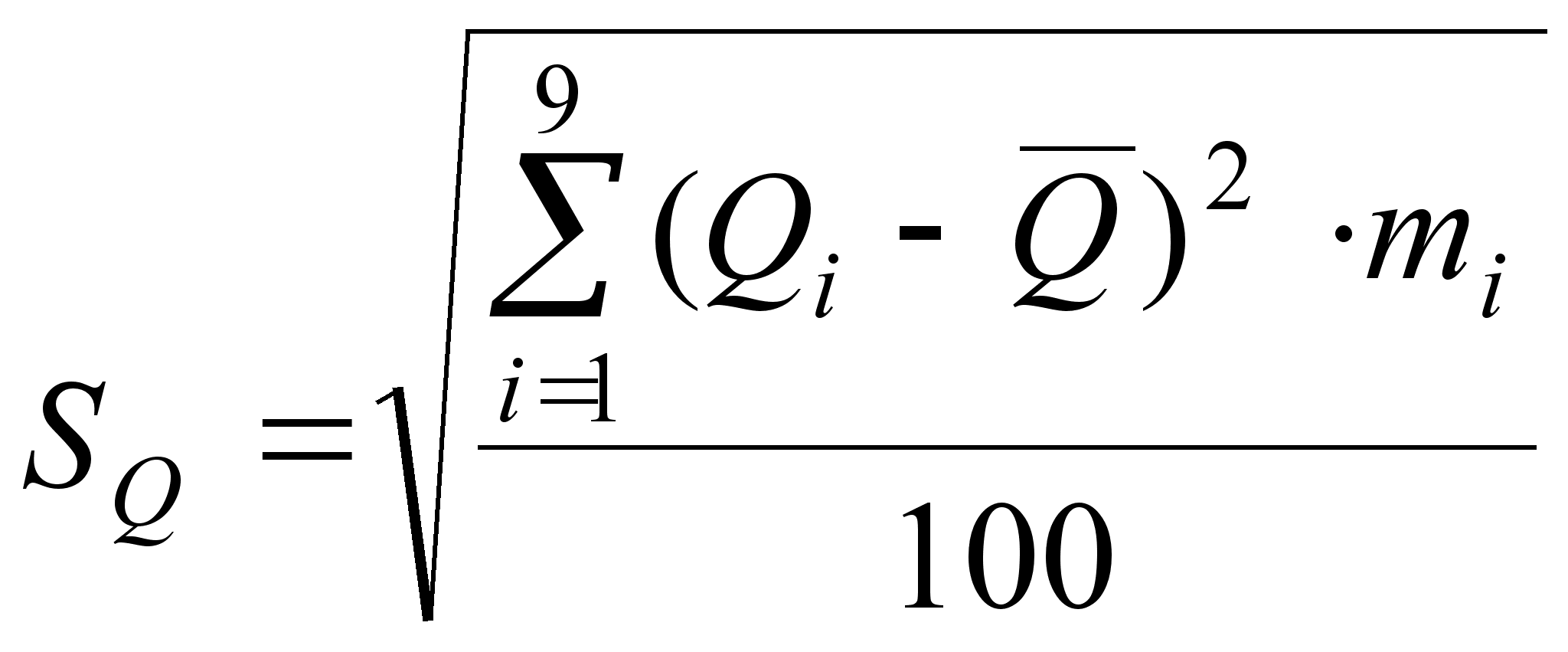 (37)
(37)
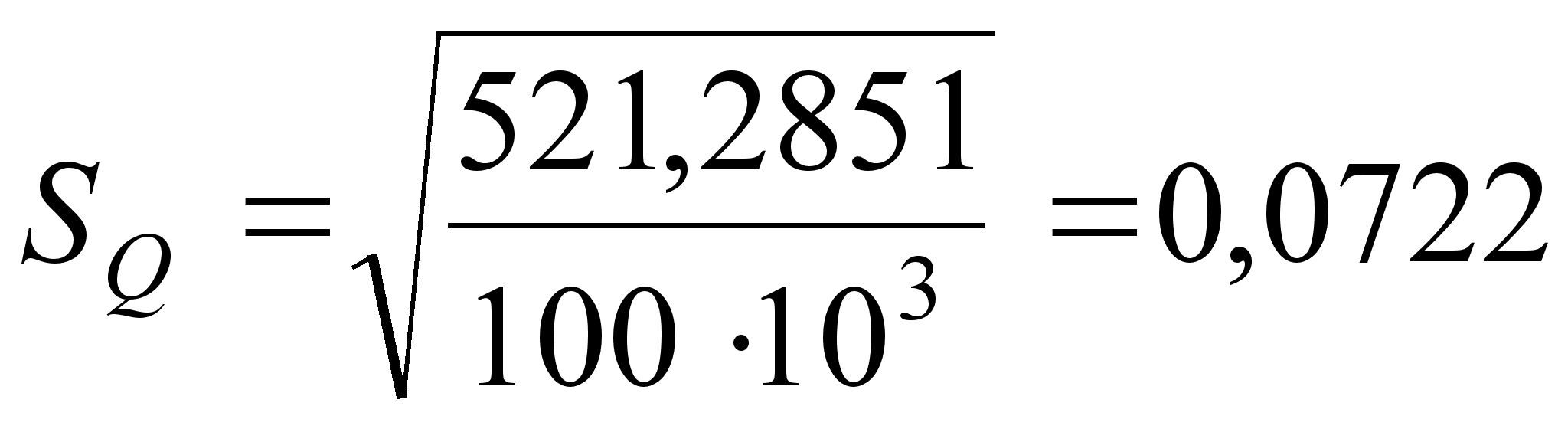
Для построения кривой нормального рассеяния определим:
1. Ymax: 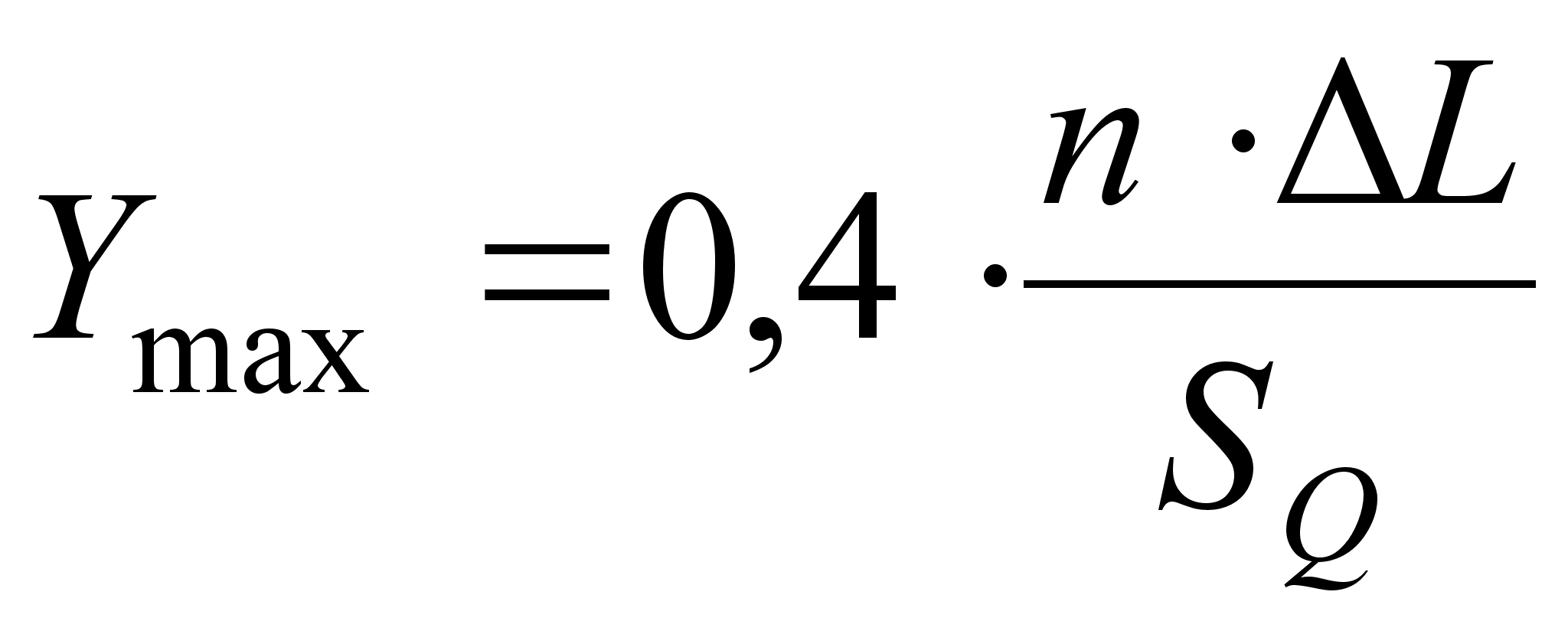 (38)
(38)
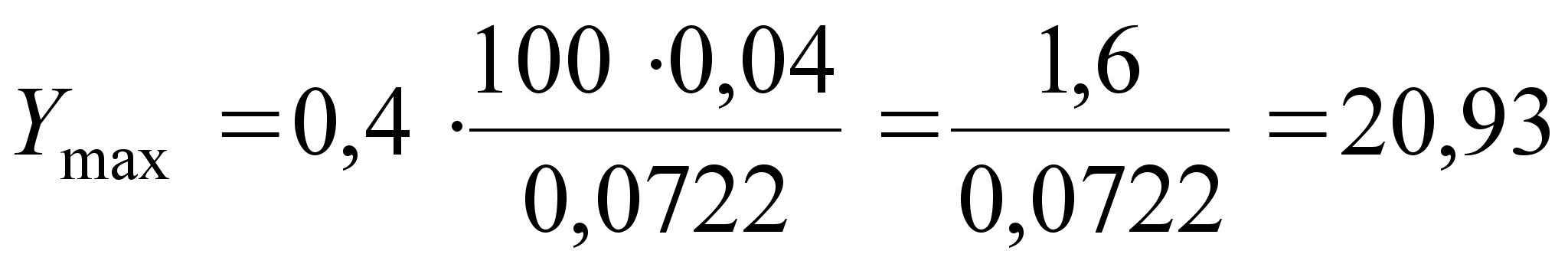
2. Y для точек перегиба (X = +σ):
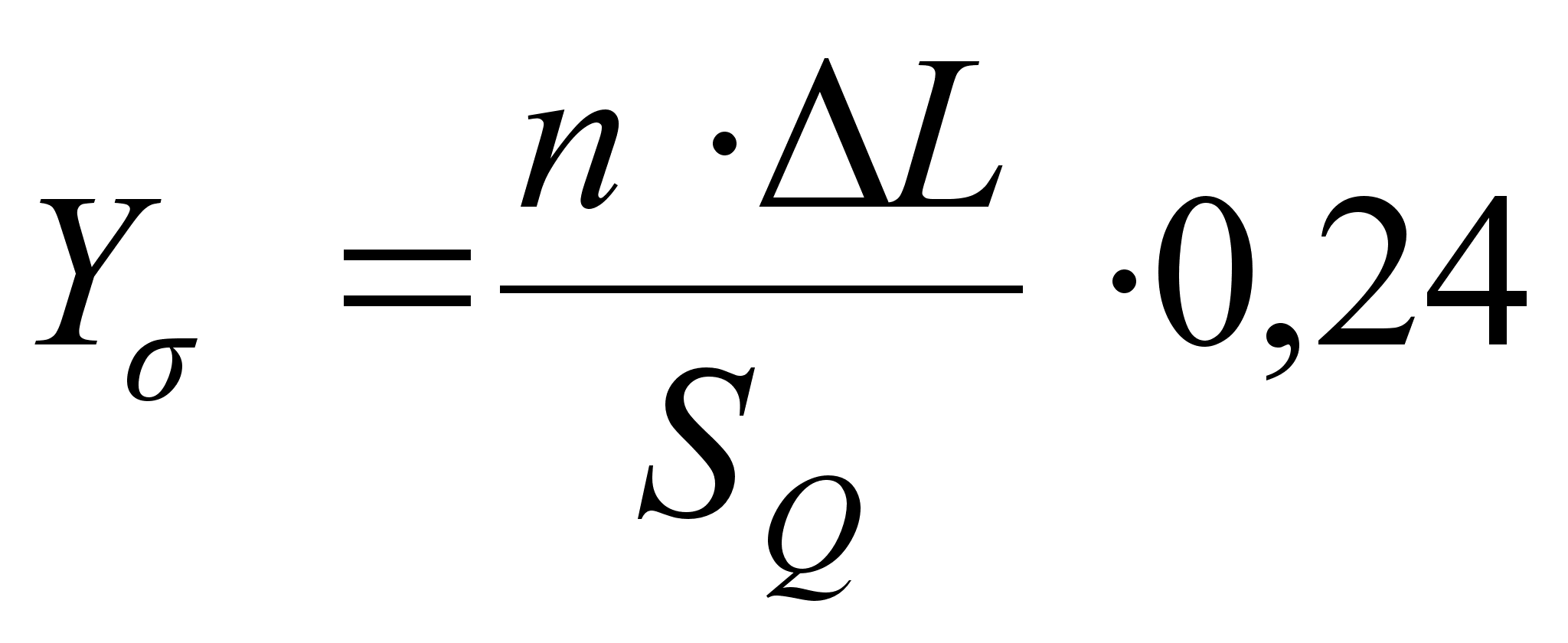 (39)
(39)
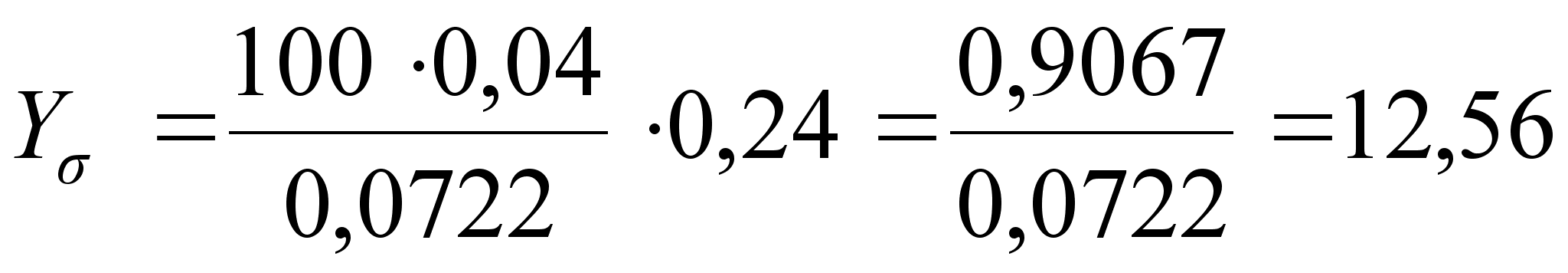
3. Величина поля рассеяния
![]()
4. Координаты кривой нормального рассеяния
![]()
![]()
![]()
![]()
По этим данным строится кривая нормального распределения непосредственно на графике рассеяния фактических значений.
Величина смещения центра поля рассеяния от середины области допустимых значений по абсциссе равна:
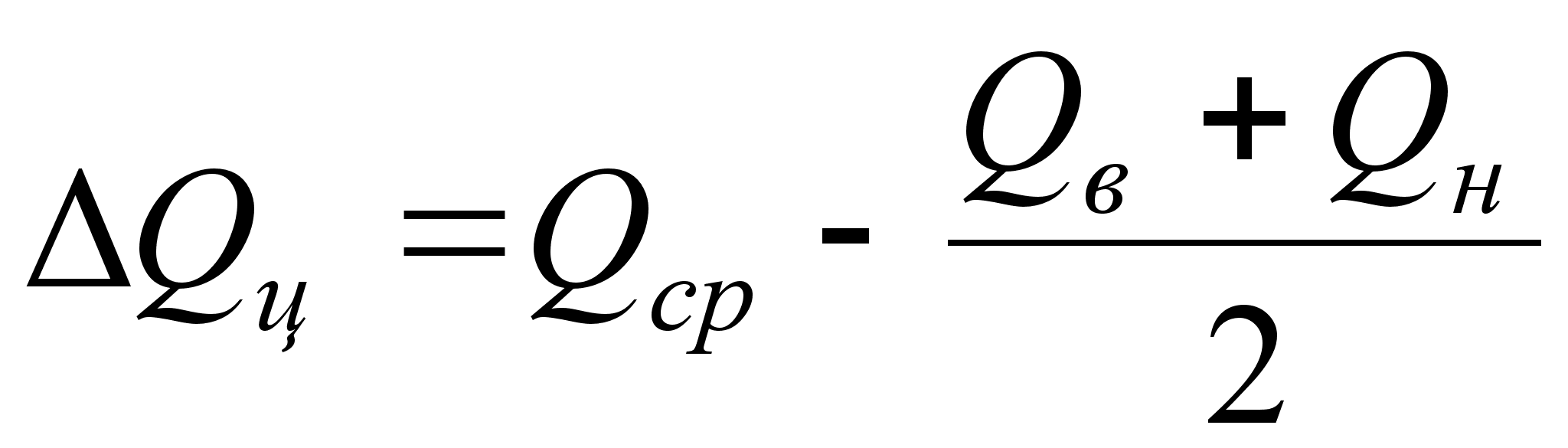 , (40)
, (40)
где: Qср – абсцисса центра поля рассеяния;
Qв – верхнее предельное значение области допустимых значений;
Qн – нижнее предельное значение области допустимых значений.
![]()
Значения аргумента для верхнего и нижнего предельно допустимых значений определим по формулам:
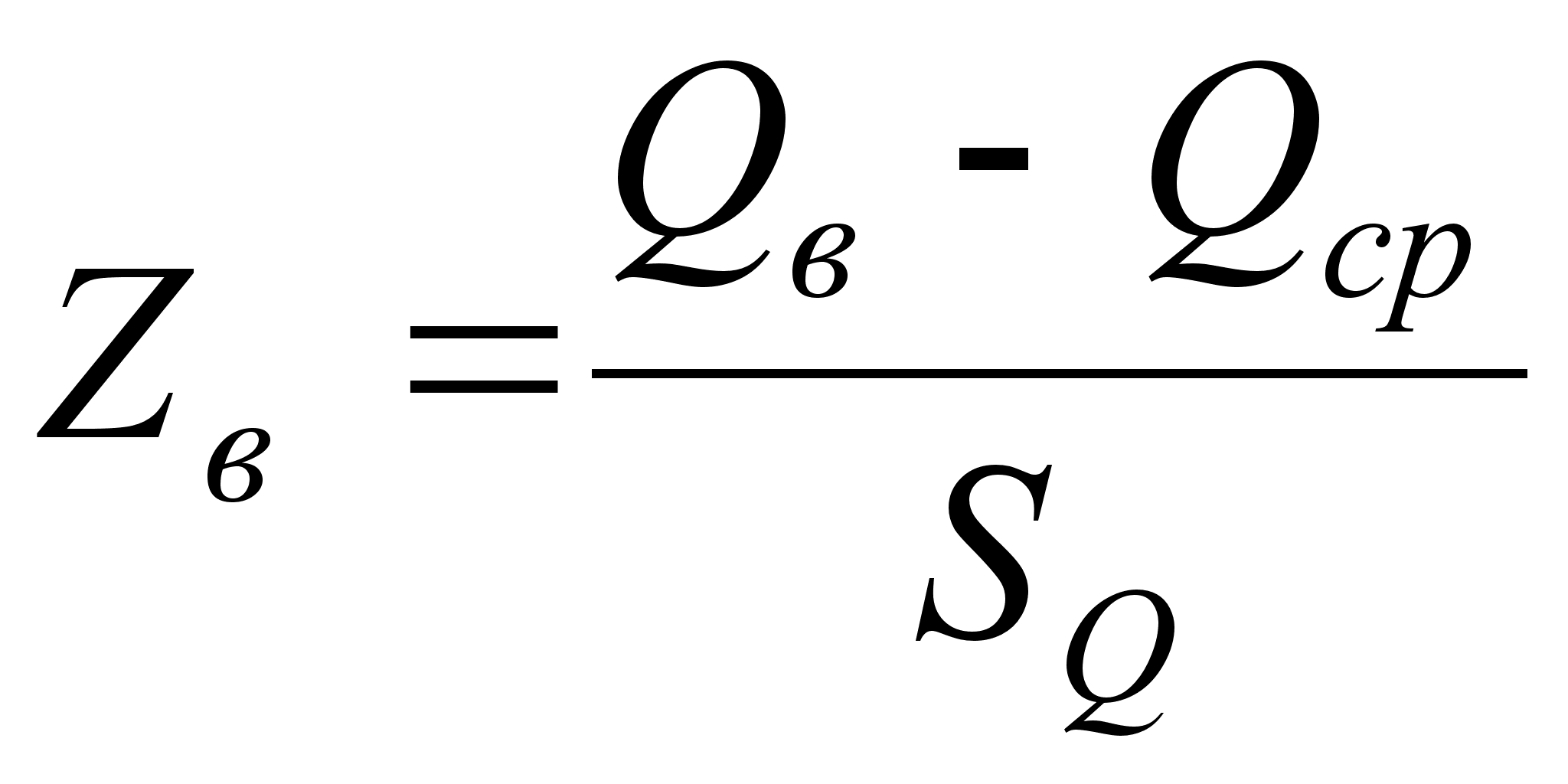 ,
, 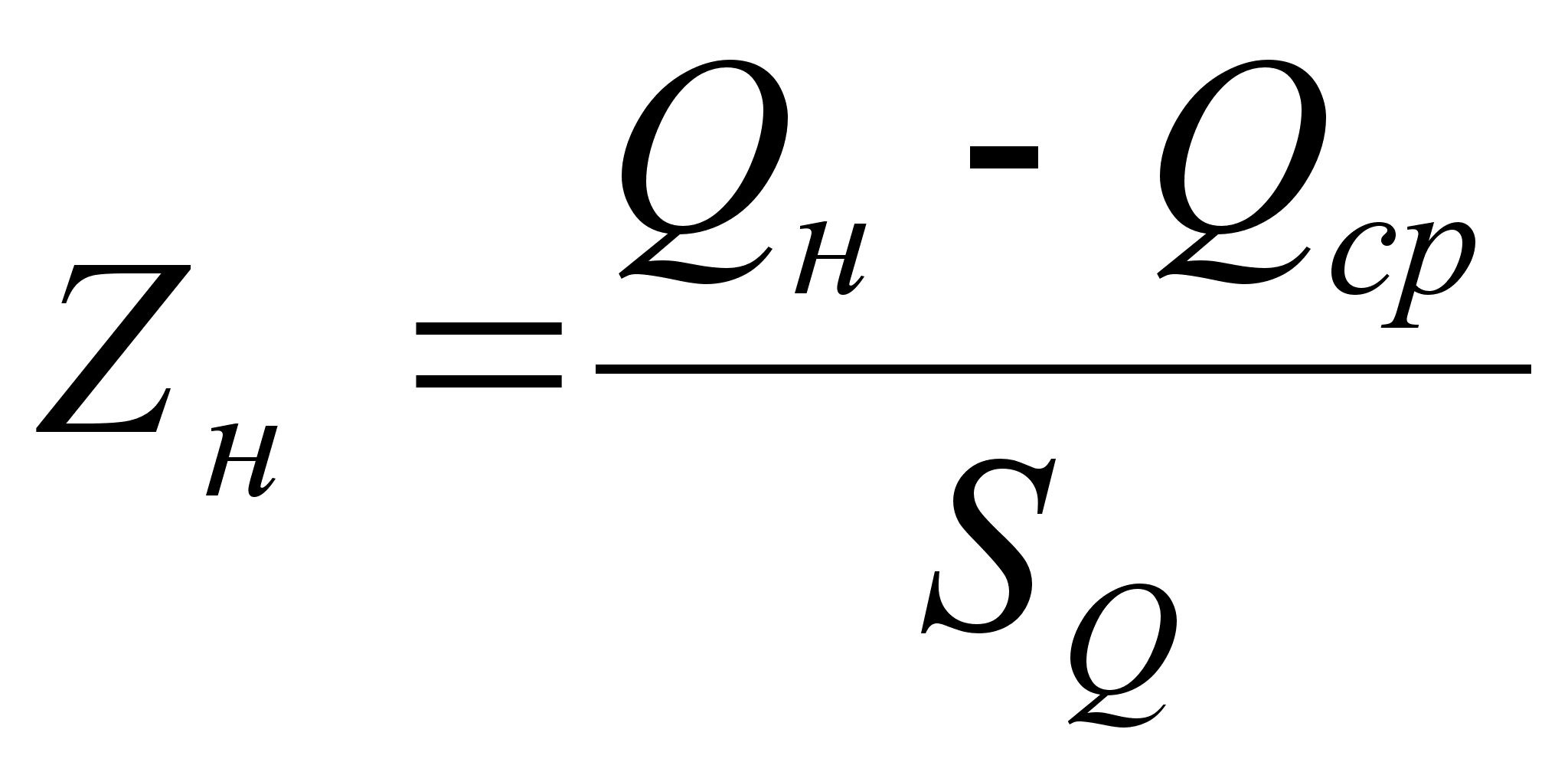 ; (41)
; (41)
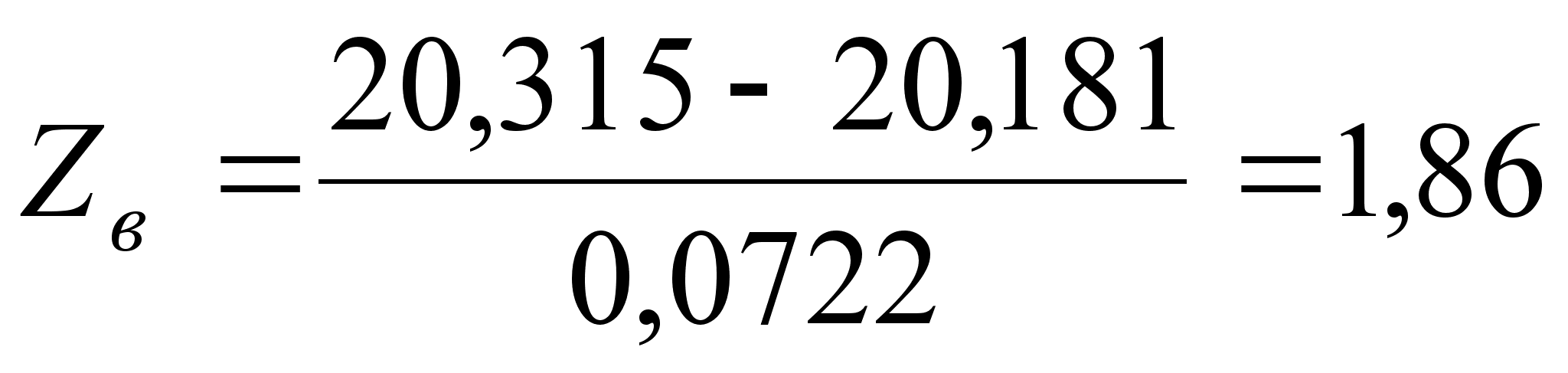 ;
; 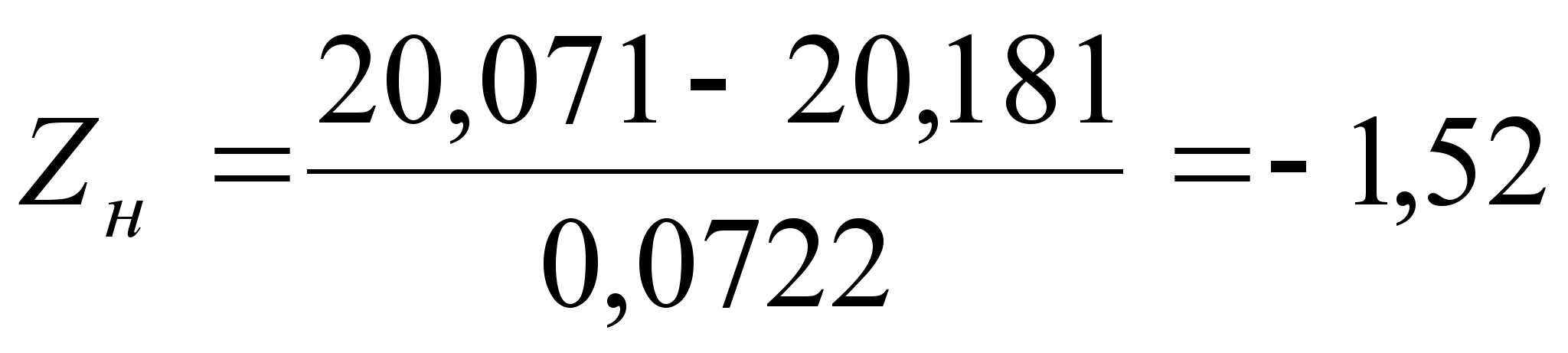 ;
;
Вероятность ошибки τ (%)
– по верхнему пределу, τв = [0,5–Ф(Zв)]·100%=[0,5–Ф(1,86)]·100%=3,14%
– по нижнему пределу, τн = [0,5–Ф(Zн)]·100%=[0,5–Ф(-1,52)]·100%=6,43%
Рис. 2. Кривая рассеяния фактических значений и
кривая нормального распределения
Литература
Шишкин И.Ф. Метрология, стандартизация и управление качеством – М.: Изд-во стандартов, 1990.
ГОСТ 8.401–80.
Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986. – 544 с.
Атамалян Э.Г. Приборы и методы измерения электрических величин. – М.: Высшая школа, 1989. – 384 с.

Курсовая работа
30
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Ливенский политехнический колледж
(филиал) Орел ГТУ
кафедра ПМиС
КУРСОВАЯ РАБОТА
по дисциплине: «Метрология, стандартизация и сертификация»
по теме: «Статистическая обработка экспериментальных данных»
Выполнил:
студент гр. 21 – с
направление 550100
курс 2
шифр 994145 ____________________Старина А.Г.
Работу проверил ____________________Бакурова Ю.А.
Оценка ___________________
Дата защиты ______________
ЛИВНЫ 2002