| Скачать .docx |
Реферат: Методические указания по выполнению практических и лабораторных работ по статистике содержат требования по их выполнению, порядок расчетов вручную и с использованием ms excel, ппп statistica.
ВВЕДЕНИЕ
Методические указания по выполнению практических и лабораторных работ по статистике содержат требования по их выполнению, порядок расчетов вручную и с использованием MS Excel, ППП Statistica.
Часть II методических указаний характеризует расчет показателей вариации: размаха вариации, квартилей и квартильного отклонения, среднего линейного отклонения, дисперсии и среднего квадратического отклонения, коэффициентов осцилляции, вариации, асимметрии, эксцесса и других.
Расчет показателей вариации наряду с построением интервальных и дискретных вариационных рядов и расчетом средних величин, представленными в части I методических указаний, имеет большое значение для анализа рядов распределения.
1. ПРАКТИЧЕСКАЯ РАБОТА №3
РАСЧЕТ ПОКАЗАТЕЛЕЙ ВАРИАЦИИ
Цель работы: получение практических навыков в расчете различных показателей (меры) вариации в зависимости от поставленных исследованием задач.
Порядок выполнения работы:
1. Определить вид и форму (простая или взвешенная) показателей вариации.
2. Рассчитать показатели степени вариации для сгруппированных и несгруппированных данных и показатели формы распределения.
3. Сформулировать выводы.
Пример расчета показателей вариации
1. Определение вида и формы показателей вариации.
Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся: размах вариации, квартильное отклонение, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Относительными показателями являются коэффициенты осцилляции, вариации, относительное линейное отклонение и т. д.
Размах вариации (R) является наиболее простым измерителем вариации признака и определяется по следующей формуле:
![]() , (1)
, (1)
где ![]() – наибольшее значение варьирующего признака;
– наибольшее значение варьирующего признака;
![]() – наименьшее значение варьирующего признака.
– наименьшее значение варьирующего признака.
Квартильное отклонение (Q) – применяется для характеристики вариации признака в совокупности. Может использоваться вместо размаха вариации во избежание недостатков, связанных с использованием крайних значений.
![]() , (2)
, (2)
где ![]() и
и ![]() – соответственно первая и третья квартили распределения.
– соответственно первая и третья квартили распределения.
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине ![]() ; 25% единиц будут заключены между
; 25% единиц будут заключены между ![]() и
и ![]() ; 25% единиц будут заключены между
; 25% единиц будут заключены между ![]() и
и ![]() , и остальные 25% превосходят
, и остальные 25% превосходят ![]() .
.
Квартили определяются по формулам:
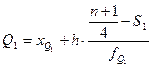 , (3)
, (3)
![]() где
где ![]() – нижняя граница интервала, в котором находится первая квартиль;
– нижняя граница интервала, в котором находится первая квартиль;
![]() – сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль;
– сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль;
![]() – частота интервала, в котором находится первая квартиль.
– частота интервала, в котором находится первая квартиль.
![]() , (4)
, (4)
где Ме – медиана ряда;
![]() , (5)
, (5)
![]() условные обозначения те же, что и для величины
условные обозначения те же, что и для величины ![]() .
.
В симметричных или умеренно асимметричных распределениях Q»2/3s. Так как на квартильное отклонение не влияют отклонения всех значений признака, то его использование следует ограничить случаями, когда определение среднего квадратического отклонения затруднительно или невозможно.
Среднее линейное отклонение (![]() ) представляет собой среднюю величину из абсолютных отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения.
) представляет собой среднюю величину из абсолютных отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения.
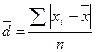 (6) - невзвешенное среднее линейное отклонение,
(6) - невзвешенное среднее линейное отклонение,
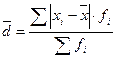 (7) - взвешенное среднее линейное отклонение.
(7) - взвешенное среднее линейное отклонение.
Дисперсия (![]() ) – средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия вычисляется по формулам простой невзвешенной и взвешенной.
) – средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия вычисляется по формулам простой невзвешенной и взвешенной.
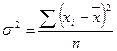 (8) - невзвешенная,
(8) - невзвешенная,![]()
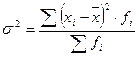 (9) - взвешенная.
(9) - взвешенная.
Среднее квадратическое отклонение (s) – наиболее распространенный показатель вариации, представляет собой квадратный корень из значения дисперсии.
![]() (10)
(10)
Размах вариации, квартильное отклонение, среднее линейное и квадратическое отклонения – величины именованные, имеют размерность осредняемого признака.
Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Чаще всего относительные показатели выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности.
Коэффициент осцилляции рассчитывается по формуле:
![]() , (11)
, (11)
Относительное линейное отклонение (линейный коэффициент вариации):
![]() , (12)
, (12)
Относительный показатель квартильной вариации:
![]() (13) или
(13) или ![]() (14)
(14)
Коэффициент вариации:
![]() , (15)
, (15)
Наиболее часто применяемый в статистике показатель относительной колеблемости – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и как характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (Ефимова М.Р., Рябцев В.М. Общая теория статистики: Учебник М.: Финансы и статистика, 1991 г., стр. 105).
Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму).
В практике статистического исследования приходится встречаться с самыми различными распределениями. При изучении однородных совокупностей имеем дело, как правило, с одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности, появление двух и более вершин говорит о необходимости перегруппировки данных с целью выделения более однородных групп. Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса. Симметричным
является распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. В связи с этим простейший показатель асимметрии
основан на соотношении показателей центра распределения: чем больше разница между средними ![]() , тем больше асимметрия ряда.
, тем больше асимметрия ряда.
Для сравнительного анализа степени асимметрии нескольких распределений рассчитывают относительный показатель As:
![]() . (16)
. (16)
Величина показателя As может быть положительной и отрицательной. Положительная величина показателя указывает на наличие правосторонней асимметрии (правая ветвь относительно максимальной ординаты вытянута больше, чем левая). При правосторонней асимметрии между показателями центра распределения существует соотношение: ![]() . Отрицательный знак показателя асимметрии свидетельствует о наличии левосторонней асимметрии (Рисунок 1). Между показателями центра распределения в этом случае имеется такое соотношение:
. Отрицательный знак показателя асимметрии свидетельствует о наличии левосторонней асимметрии (Рисунок 1). Между показателями центра распределения в этом случае имеется такое соотношение: ![]() .
.
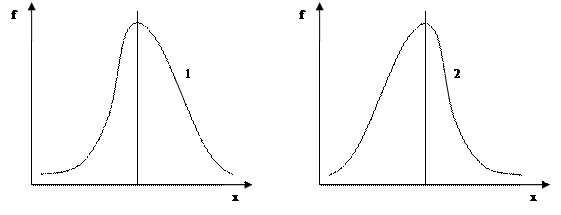 |
Рисунок 1 – Распределение: 1 – с правосторонней асимметрией; 2 – с левосторонней асимметрией.
Другой показатель, предложенный шведским математиком Линдбергом, рассчитывают по формуле:
![]()
![]() , (17)
, (17)
где П – процент тех значений признака, которые превосходят по величине среднюю арифметическую.
Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна нулю):
![]() , (18)
, (18)
где ![]() - центральный момент третьего порядка:
- центральный момент третьего порядка:
![]() (19) - для несгруппированных данных;
(19) - для несгруппированных данных;
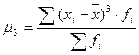 (20) - для сгруппированных данных.
(20) - для сгруппированных данных.
σ – среднеквадратическое отклонение.
Применение этого показателя дает возможность не только определить величину асимметрии, но и ответить на вопрос о наличии или отсутствии асимметрии в распределении признака в генеральной совокупности. Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений n и рассчитывается по формуле:
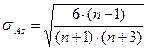 . (21)
. (21)
Если отношение ![]() , асимметрия существенна, и распределение признака в генеральной совокупности не является симметричным. Если отношение
, асимметрия существенна, и распределение признака в генеральной совокупности не является симметричным. Если отношение ![]()
![]() , асимметрия несущественна, ее наличие может быть объяснено влиянием различных случайных обстоятельств.
, асимметрия несущественна, ее наличие может быть объяснено влиянием различных случайных обстоятельств.
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Линдбергом предложен следующий показатель для оценки эксцесса:
![]() , (22)
, (22)
где П – доля (%) количества вариантов, лежащих в интервале, равном половине среднего квадратического отклонения в ту или другую сторону от средней арифметической.
Наиболее точным является показатель, использующий центральный момент четвертого порядка:
![]() , (23)
, (23)
где ![]() - центральный момент четвертого момента;
- центральный момент четвертого момента;
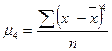 (24) - для несгруппированных данных;
(24) - для несгруппированных данных;
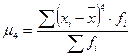 (25) - для сгруппированных данных.
(25) - для сгруппированных данных.
На рисунке 2 представлены два распределения: одно – островершинное (величина эксцесса положительная), второе – плосковершинное (величина эксцесса отрицательная). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. В нормальном распределении отношение ![]() .
.
 |
Рисунок 2 – Распределение: 1,4 – нормальное; 2 – островершинное; 3 – плосковершинное
Средняя квадратическая ошибка эксцесса рассчитывается по формуле:
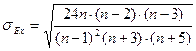 , (26)
, (26)
где n – число наблюдений.
Если ![]() , то эксцесс существенен, если
, то эксцесс существенен, если ![]() , то несущественен.
, то несущественен.
Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое исследование к типу кривых нормального распределения.
2. Рассмотрим методику исчисления показателей вариации.
Пример 1.
Таблица 1 - Данные об объеме продаж валюты нескольких отделений Центробанка.
| Номер отделения |
Объем продаж, млн. руб. |
| 1 |
10,2 |
| 2 |
15,7 |
| 3 |
24,3 |
| 4 |
17,5 |
| 5 |
16,8 |
| 6 |
19,2 |
| 7 |
15,4 |
Определить средний объем продаж валюты по совокупности отделений, рассчитать абсолютные и относительные показатели вариации.
Рассчитаем размах вариации:
R = ![]() = 24,3 - 10,2 = 14,1 млн. руб.
= 24,3 - 10,2 = 14,1 млн. руб.
Для определения отклонений значений признака от средней и их квадратов строим вспомогательную таблицу:
Таблица 2 – Расчетная таблица
| Номер отделения |
|
|
|
| 1 |
10,2 |
-6,81 |
46,38 |
| 2 |
15,7 |
-1,31 |
1,72 |
| 3 |
24,3 |
7,29 |
53,14 |
| 4 |
17,5 |
0,49 |
0,24 |
| 5 |
16,8 |
-0,21 |
0,04 |
| 6 |
19,2 |
2,19 |
4,80 |
| 7 |
15,4 |
1,61 |
2,59 |
| Итого |
119,1 |
108,91 |
Среднее значение находим по формуле средней арифметической простой:
![]() млн. руб.
млн. руб.
Среднее линейное отклонение:
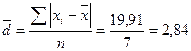 млн. руб.
млн. руб.
Дисперсия:
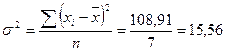
Среднее квадратическое отклонение:
![]() млн. руб.
млн. руб.
Рассчитаем относительные показатели вариации.
Коэффициент осцилляции:
![]()
Относительное линейное отклонение:
![]()
Коэффициент вариации:![]()
![]()
![]() Для расчета показателей формы распределения строим вспомогательную таблицу:
Для расчета показателей формы распределения строим вспомогательную таблицу:
Таблица 3 – Расчетная таблица
|
|
|
|
|
| 10,2 |
-6,81 |
-315,82 |
2150,743 |
| 15,7 |
-1,31 |
-2,25 |
2,945 |
| 24,3 |
7,29 |
387,42 |
2824,295 |
| 17,5 |
0,49 |
0,12 |
0,058 |
| 16,8 |
-0,21 |
-0,01 |
0,002 |
| 19,2 |
2,19 |
10,50 |
23,003 |
| 15,4 |
-1,61 |
-4,17 |
6,719 |
| 75,79 |
5007,764 |
Далее рассчитываем показатели асимметрии, эксцесса и их ошибки:
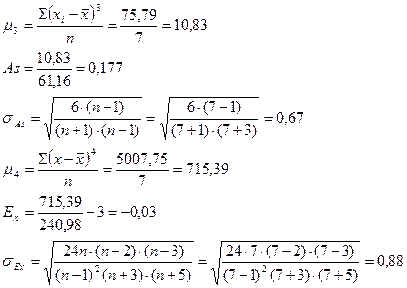
Пример 2.
Таблица 4 - Данные о товарообороте предприятий одной из отраслей промышленности.
| Группы предприятий по объему товарооборота |
Число предприятий |
| 10-15 |
3 |
| 15-20 |
7 |
| 20-25 |
10 |
| 25-30 |
18 |
| 30-35 |
22 |
| 35-40 |
12 |
| 40-45 |
5 |
| 45-50 |
3 |
| Итого |
80 |
Определить средний объем товарооборота, структурные средние, абсолютные и относительные показатели вариации и насколько фактическое распределение согласуется с нормальным (по показателям формы распределения).
Для расчета показателей построим вспомогательную таблицу.
Таблица 5 – Расчетная таблица
|
|
|
|
|
|
|
|
|
|
| 12,5 |
3 |
3 |
37,5 |
-17,5 |
52,5 |
918,8 |
-16078,13 |
281367,2 |
| 17,5 |
7 |
10 |
122,5 |
-12,5 |
87,5 |
1093,8 |
-13671,88 |
170898,4 |
| 22,5 |
10 |
20 |
225,0 |
-7,5 |
75,0 |
562,5 |
-4218,75 |
31640,6 |
| 27,5 |
18 |
38 |
495,0 |
-2,5 |
45,0 |
112,5 |
-281,25 |
703,1 |
| 32,5 |
22 |
60 |
715,0 |
2,5 |
55,0 |
137,5 |
343,75 |
859,4 |
| 37,5 |
12 |
72 |
450,0 |
7,5 |
90,0 |
675,0 |
5062,50 |
37968,8 |
| 42,5 |
5 |
77 |
212,5 |
12,5 |
62,5 |
781,3 |
9765,63 |
122070,3 |
| 47,5 |
3 |
80 |
142,5 |
17,5 |
52,5 |
918,8 |
16078,13 |
281367,2 |
| Итого |
80 |
2400 |
520 |
5200 |
-3000,00 |
926875,0 |
Размах вариации:
![]() млн. руб.
млн. руб.
Среднее значение находим по формуле средней арифметической взвешенной:
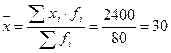 млн. руб.
млн. руб.
В интервальных рядах распределения мода определяется по формуле:
![]() (27)
(27)
В нашем случае мода будет равна:
![]() млн. руб.
млн. руб.
В интервальном вариационном ряду медиана определяется по формуле:
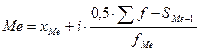 (28)
(28)
В нашем случае медиана будет равна:
![]() млн. руб.
млн. руб.
Квартильное отклонение:
![]() млн. руб.
млн. руб.
где ![]() и
и ![]() – соответственно первая и третья квартили распределения.
– соответственно первая и третья квартили распределения.
Квартили определяются по формулам:
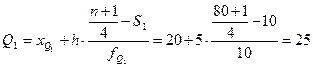 млн. руб.
млн. руб.
![]() млн. руб.
млн. руб.
![]() млн. руб.
млн. руб.
Среднее линейное отклонение:
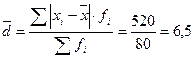 млн. руб.
млн. руб.
Дисперсия:
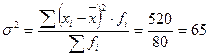
Среднее квадратическое отклонение:
![]() млн. руб.
млн. руб.
Рассчитаем относительные показатели вариации.
Коэффициент осцилляции:
![]()
Относительное линейное отклонение:
![]()
Относительный показатель квартильной вариации:
![]()
Коэффициент вариации:
![]()
Определим показатели формы распределения:
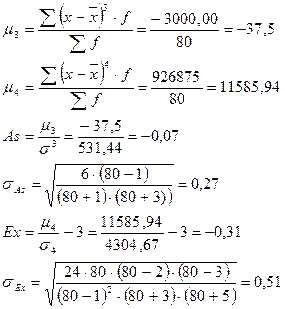
3. Формулировка выводов.
Сформулируем выводы по рассчитанным показателям вариации примера 2, в котором представлен интервальный ряд распределения предприятий по объему товарооборота, млн. руб.
Размах вариации свидетельствует о том, что разница между максимальным и минимальным значением составляет 40 млн. руб. Средний объем товарооборота – 30 млн. руб. Чаще всего встречающееся значение объема товарооборота в рассматриваемой совокупности предприятий – 31,4 млн. руб., причем 50% (40 предприятий) имеют объем товарооборота менее 30,5 млн. руб., а 50% свыше.
Квартильное отклонение, равное 5, свидетельствует об умеренной асимметрии распределения, так как в симметричных или умеренно асимметричных распределениях ![]() (в рассматриваемом примере
(в рассматриваемом примере ![]() ).
).
Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности. Так, средняя величина колеблемости объема товарооборота предприятий отраслей промышленности составляет: по среднему линейному отклонению - 6,5 млн. руб. (абсолютное отклонение); по среднему квадратическому отклонению - 8,1 млн. руб. Квадрат отклонений индивидуальных значений признака от их средней величины равен 65.
Разница между крайними значениями признака на 33,3% превышает среднее значение (![]() = 133,3%).
= 133,3%).
Относительное линейное отклонение (![]() = 21,7%) и относительный показатель квартильной вариации (
= 21,7%) и относительный показатель квартильной вариации (![]() = 16,4%) характеризуют однородность исследуемой совокупности, что подтверждает рассчитанный коэффициент вариации, равный 27% (V =27% меньше 33%).
= 16,4%) характеризуют однородность исследуемой совокупности, что подтверждает рассчитанный коэффициент вариации, равный 27% (V =27% меньше 33%).
По рассчитанным показателям асимметрии и эксцесса можно сделать вывод, что распределение плосковершинно (Ex < 0) и наблюдается левосторонняя асимметрия (As < 0). Асимметрия и эксцесс являются несущественными.
2. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Таблица 6 - Данные о производительности труда 10 рабочих
| Произведено продукции одним рабочим за смену, штук |
||||||
| Табельный номер рабочего |
1 вариант |
2 вариант |
3 вариант |
4 вариант |
5 вариант |
6 вариант |
| 1 |
11 |
23 |
43 |
63 |
85 |
59 |
| 2 |
15 |
27 |
49 |
75 |
96 |
48 |
| 3 |
18 |
34 |
45 |
81 |
79 |
56 |
| 4 |
10 |
37 |
47 |
63 |
85 |
39 |
| 5 |
11 |
37 |
45 |
58 |
90 |
56 |
| 6 |
14 |
25 |
43 |
63 |
78 |
61 |
| 7 |
13 |
27 |
45 |
71 |
85 |
59 |
| 8 |
11 |
37 |
48 |
75 |
76 |
47 |
| 9 |
9 |
34 |
39 |
71 |
69 |
60 |
| 10 |
15 |
25 |
51 |
63 |
90 |
54 |
Рассчитать показатели вариации и показатели формы распределения, сделать соответствующие выводы.
Таблица 7 – Данные о распределении населения по уровню среднедушевых денежных доходов в регионах страны
| Среднедушевой денежный доход в месяц, руб. |
Численность населения, тыс. чел. |
|||||
| 1 вариант |
2 вариант |
3 вариант |
4 вариант |
5 вариант |
6 вариант |
|
| до 800 |
12,7 |
10,2 |
13,1 |
30,3 |
15,4 |
2,3 |
| 800-1000 |
16,7 |
13,4 |
18,2 |
60,7 |
39,4 |
16,7 |
| 1000-1200 |
25,1 |
18,5 |
29,4 |
110,5 |
78,1 |
24,4 |
| 1200-1400 |
19,4 |
23,5 |
20,5 |
182,5 |
159,2 |
430,2 |
| 1400-1600 |
10,5 |
36,7 |
17,2 |
70,6 |
198,5 |
10,5 |
| 1600-1800 |
6,5 |
19,1 |
10,1 |
54,8 |
156,4 |
6,5 |
| 1800-2000 |
2,7 |
13,5 |
5,2 |
32,1 |
54,1 |
6,7 |
| 2000 и выше |
1,3 |
4,2 |
5,1 |
15,7 |
24,9 |
2,7 |
Определить показатели вариации и показатели формы распределения, сделать соответствующие выводы.