| Скачать .docx | Скачать .pdf |
Реферат: Преобразование Фурье
Kalmiik-forever
Глава I
Преобразование Фурье.
§1. Класс Шварца.
Преобразование Фурье отображает класс Шварца на себя.
Определение . Следующее множество комплекснозначных функций действительного переменного называется классом Шварца.
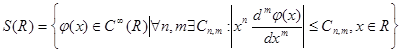 .
.
Класс Шварца иногда называют классом быстро убывающих функций.
Операции обычного сложения и умножения функции на число превращают класс Шварца в линейное векторное пространство:
"j,yÎS(R), a, bÎКвыполнено aj+byÎS(R).
Отметим несколько простых свойств функций из класса Шварца.
1) Если j(x)ÎS(R),то ![]()
2) Если j(x)ÎS(R),то j(x) ограничена на R.
3) Еслиj(x)ÎS(R),тоy(x)=xj(x)ÎS.
4) Если j(x)ÎS(R) и P(x) – многочлен, то P(x)j(x)ÎS.
5) Если j(x)ÎS(R),то ![]() .
.
Доказательство. Первые два свойства сразу следуют из неравенств
![]() .
.
Докажем свойство 3). Во первых, y=xjÎC∞ (R). Далее,
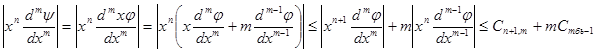 .
.
Свойство 4) получается из 3) последовательным применением. В самом деле, если P(x)=a0 +a1 x+…+an xn , то по свойству 3) имеем xi jÎS(R), потому функция P(x)j(x)=a0 j+a1 (xj)+a2 (x2 j)+…+an (xn j) принадлежит классу Шварца ввиду его линейности.
Свойство 5) доказывается аналогично свойству 3).
§2. Одномерное преобразование Фурье.
Определение. Функция
![]() (1)
(1)
называется преобразованием Фурье функции j(x) и обозначается F[j]. Ясно, что не для всякой функции j(x) интеграл (1) сходится, и потому не для всякой функции определено преобразование Фурье.
Если ![]() (интеграл Лебега), то будем говорить, что j принадлежит пространству L1
(R).
(интеграл Лебега), то будем говорить, что j принадлежит пространству L1
(R).
Предложение 1. Преобразование Фурье функции j(x) из L1 (R) определено и ограничено по модулю на действительной оси.
Доказательство следует из равенства ![]() и (1):
и (1):
![]()
Следствие. Преобразование Фурье определено для функций jÎS(R).
Доказательство. Достаточно доказать, что S(R)ÌL1 (R). Заметим, что если jÎS(R), то по свойству 4) функция (1+x2 )jÎS(R) и, следовательно, ограничена, а (1+x2 )-1 ÎL1 (R). Поэтому функция (1+x2 )j(1+x2 )-1 ÎL1 (R).
§3. Свойства преобразований Фурье функций из S ( R ).
1) ![]()
Доказательство получается дифференцированием в (1) под знаком интеграла. Это законно, так как интеграл, полученный после дифференцирования, мажорируется интегралом
![]()
сходимость которого вытекает из свойства 3): xj(x)ÎS(R)ÌL1 (R).
2) Если jÎS(R), то F[j]ÎC¥ (R).
Так как -ixjÎS, то доказательство немедленно вытекает из 1).
3) ![]()
Доказательство. Очевидно
![]()
теперь можно интегрировать по частям
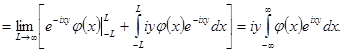
Это и доказывает свойство 3).
Предложение 2. Преобразование Фурье функции из класса Шварца есть снова функция из класса Шварца.
Доказательство. Многократно применяя свойства 1) и 3), устанавливаем
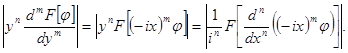
По свойствам 4) и 5) класса Шварца функция
![]()
лежит в классе Шварца SÌL1
, и тогда, по предложению пункта 2, функция ![]() ограничена некоторой постоянной, которую мы обозначим Cn
,
m
. Предложение доказано.
ограничена некоторой постоянной, которую мы обозначим Cn
,
m
. Предложение доказано.
§4. Обратное преобразование Фурье.
Определение . Функция
![]()
называется обратным преобразованием Фурье функции j(y) и обозначается F-1 [j].
Нетрудно проверить, что обратное преобразование Фурье функций из S(R) обладает свойствами, аналогичными прямому:
1) ![]()
2) ![]()
3) ![]()
Докажем, что F-1 [F[j]]=j для любой функции jÎS. Для этого потребуется
Лемма. Пусть непрерывная функция h(y)ÎL1 (R) имеет почти всюду ограниченную производную. Пусть
![]()
такой набор точек, что на интервалах (yi ,yi +1 ) функция h класса C2 , i=1,2,…,n. Тогда для всех x, отличных от yi , i=1,2,…,n+1, справедливо соотношение
![]()
Доказательство. Так как h(y)ÎL1 , то для всякого e>0 найдется такое А, что
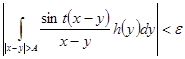
при всех t>0. Заметим, что
![]() (3)
(3)
Тогда
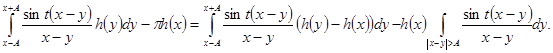
Второе слагаемое в (4) заменой z= t(x - y) приводится к виду
![]()
и, следовательно, стремится к нулю при ![]() в силу сходимости интеграла (3). Для доказательства леммы осталось показать, что первое слагаемое в (4) также стремится
в силу сходимости интеграла (3). Для доказательства леммы осталось показать, что первое слагаемое в (4) также стремится ![]() .
.
Введем обозначение
![]()
Если h класса C2 в окрестности точки x, то из равенства
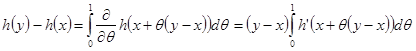
следует дифференцируемость функции g(y) в точке y = x. Итак, g(y) – кусочно-диференцируемая функция. Интегрируя по частям, устанавливаем
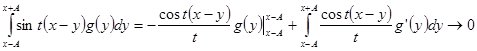
при ![]() Лемма доказана.
Лемма доказана.
Предложение 3. F-1 [F[j]]=j для любого jÎS(R).
Доказательство.
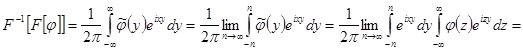
Внутренний интеграл сходится равномерно по yÎ[-n, n], поэтому возможна замена порядка интегрирования.
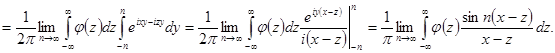
Теперь утверждение следует из леммы.
Из доказанного предложения вытекает, что преобразование Фурье взаимно-однозначно отображает класс Шварца в себя. Покажем что это отображение “на”. Определим оператор J переводящий функцию j(x) в функцию j(-x). Тогда очевидно равенство F=2pJF-1
, откуда, умножая справа на FJ/2p и используясь равенством JJ=1, будем иметь ![]() , где 1 справа надо понимать как тождественное отображение в S(R). Последнее равенство означает, что любая функция из S(R) есть преобразование Фурье некоторой функции.
, где 1 справа надо понимать как тождественное отображение в S(R). Последнее равенство означает, что любая функция из S(R) есть преобразование Фурье некоторой функции.
§5. Класс Шварца в многомерном случае.
Мультииндексом a=(a1
,…,an
) будем называть набор из неотрицательных целых чисел. Порядком мультииндекса будем называть число ![]()
Глава II
Задача Коши для уравнения теплопроводности.
§ 1. Постановка задачи коши для уравнения теплопроводности.
Требуется найти функцию u
(
x
,
t
)
, непрерывную при t![]() 0
и x
0
и x![]() R
и класса C
2
при t
>0
, удовлетворяющую уравнению
R
и класса C
2
при t
>0
, удовлетворяющую уравнению
![]() (1)
(1)
при t
>0
, x![]() R
и начальному условию
R
и начальному условию
u(x,0)= j (x) . (2)
Задача (1),(2) имеет, вообще говоря, много решений. Поэтому обычно накладывают дополнительное условие, которому должно удовлетворять решение.
Теорема (Тихонова). Пусть u ( x , t ) – решение задачи (1),(2) с функцией j(x)º0. Пусть " e >0 существует постоянная C >0 такая, что
![]()
при всех x Î R и t ³ 0 . Тогда u º 0 .
Из этой теоремы следует, что при среди функций, растущих, грубо говоря, медленнее чем ![]() при любом e
>0
, не может найтись более одного решения задачи (1),(2).
при любом e
>0
, не может найтись более одного решения задачи (1),(2).
Эту теорему мы приводим без доказательства, но ниже докажем теорему единственности при более сильных ограничениях.
§2. Формальный поиск решения.
Применим преобразование Фурье
![]()
![]() (3)
(3)
Выкладки этого пункта будем проделывать, не заботясь об обосновании. Дифференцируя (3) по t, устанавливаем:
![]()
Кроме того, по свойству 3) преобразования Фурье

Учитывая (1), имеем
![]() (4)
(4)
Решая это обыкновенное дифференциальное уравнение с параметром y , находим
![]()
![]()
Где g( y) – произвольная функция. Используя (2), определяем g( y) :
![]()
§3. Решение задачи Коши с начальной функцией из класса Шварца.
Теорема 2. Если jÎS(R), то формула
![]() (5)
(5)
дает решение задачи (1), (2), бесконечно дифференцируемое при t³0.
Доказательство. Так как ![]() , то
, то ![]() при любом t³0 и обратное преобразование Фурье в формуле (5) определено. Дифференцируя (5) по t, имеем
при любом t³0 и обратное преобразование Фурье в формуле (5) определено. Дифференцируя (5) по t, имеем
![]() (6)
(6)
так как ![]() , то интеграл (6) сходится равномерно при t³0, и дифференцирование законно. Совершенно так же доказывается бесконечная дифференцируемость функции u(
x,
t)
по t
и x
.
, то интеграл (6) сходится равномерно при t³0, и дифференцирование законно. Совершенно так же доказывается бесконечная дифференцируемость функции u(
x,
t)
по t
и x
.
Дифференцируя (5) дважды по x, устанавливаем:
![]() (7)
(7)
Из формул (6),(7) вытекает, что функция u( x, t) удовлетворяет уравнению (1). Справедливость условия (2) очевидна. Теорема доказана.
§4. Фундаментальное решение уравнения теплопроводности.
Преобразуем формулу (5) к более удобному ”явному” виду. Для этого запишем ее в интегралах
![]()
меняем порядок интегрирования
![]() (8)
(8)
В формуле (8) внутренний интеграл есть преобразование Фурье от функции ![]() при значении аргумента –(
x-
z)
, поэтому из (9.2) имеем
при значении аргумента –(
x-
z)
, поэтому из (9.2) имеем
![]()
Подставляя это в (8), получим
![]() (9)
(9)
Функцию
![]()
называют фундаментальным решением уравнения теплопроводности. Легко проверяются следующие свойства этой функции:
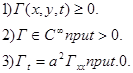
§5. Решение задачи с непрерывной ограниченной начальной функцией.
Теорема 3. Пусть j(z) ограничена и непрерывна на вещественной оси. Тогда формула (9) дает решение задачи (1),(2).
Доказательство. Продифференцируем (9) под знаком интеграла
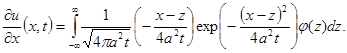 (10)
(10)
Чтобы обосновать законность такого дифференцирования, достаточно показать равномерную сходимость по x интеграла (10), для чего произведем замену
![]()
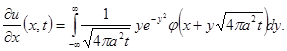
Из ограниченности функции j следует равномерная сходимость интеграла как по xÎR, так и по t>e.
Совершенно так же доказывается бесконечная дифференцируемость функции u(x, t) по x и t при t>0. Из свойства 3) фундаментального решения следует, что u есть решение уравнения (1).
Для доказательства (2) снова сделаем замену переменной интегрирования в (9):
![]()
Так как последний интеграл сходится равномерно по x и t, то возможен предельный переход под знаком интеграла
![]()
Теорема доказана.
§6. Единственность решения в классе ограниченных функций.
Теорема 4. Пусть ограниченная функция u(x, t) является решением задачи (1), (2) с начальной функцией jº0. Тогда u(x, t)º0.
Доказательство. Рассмотрим функцию
u(x, t)=e(x2 +3a2 t)+du(x, t),
где e>0, d - любого знака. Легко проверить, что
![]() (11)
(11)
Так как функция u ограничена, то функция v(x, y) в области t>0 достигает минимума в некоторой точке (x0 , t0 ). Покажем, что v(x0 , t0 )³0. Пусть, напротив v(x0 , t0 )<0. Тогда, очевидно, t0 >0, так как v(x, 0)º0. Как необходимые условия минимума имеем соотношения
![]()
которые противоречат (11).
Итак, v(x, t)³0 при всех x и t³0. При фиксированных x и t,переходя к пределу при e®0 в неравенстве
e(x2 +3a2 t)+du(x, t)³0,
получаем du(x, y)³0. Ввиду произвольности знака d отсюда следует u=0.Теорема доказана