| Скачать .docx | Скачать .pdf |
Реферат: Математический анализ. Регрессия
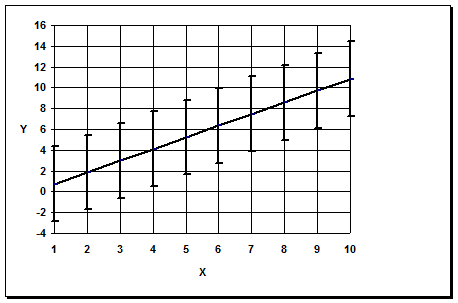
y=a уравнение регрессии.
Таблица 1
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 1.35 | 1.09 | 6.46 | 3.15 | 5.80 | 7.20 | 8.07 | 8.12 | 8.97 | 10.66 |
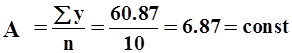
Оценка значимости коэффициентов регрессии.
Выдвигается и проверяется гипотеза о том что истинное значение коэффициента регрессии=0.
Для проверки гипотезы используется критерий Стьюдента.
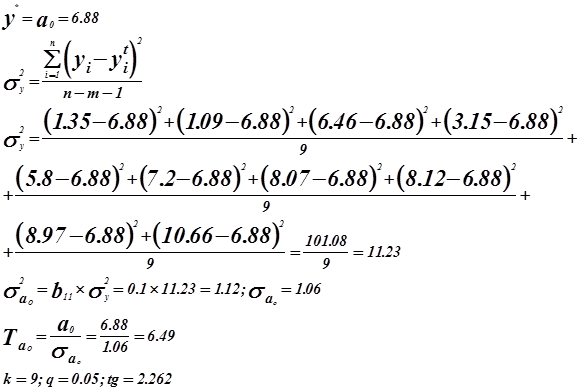
к-т является значимым и нулевую гипотезу отвергаем.
График 1
- уравнение регрессии
Таблица 2
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 1.35 | 1.09 | 6.46 | 3.15 | 5.80 | 7.20 | 8.07 | 8.12 | 8.97 | 10.66 |
Запишем матрицу X
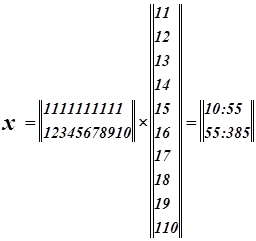
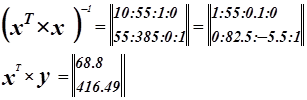
Система нормальных уравнений.
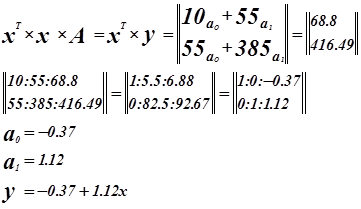
Оценка значимости коэффициентов регрессии.
Для проверки нулевой гипотезы используется критерий Стьюдента..
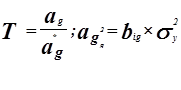
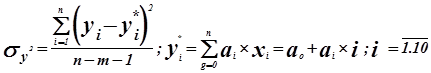
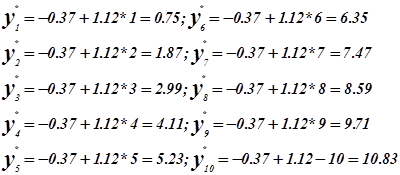
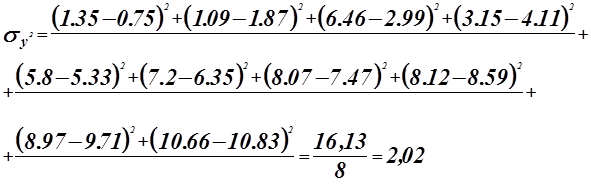
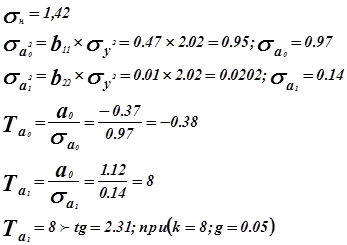
Коэффициент ai является значимости, т.к. не попал в интервал.
Проверка адекватности модели по критерию Фишера.
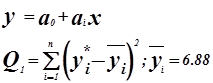
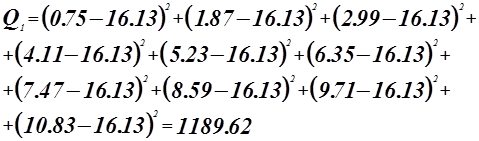
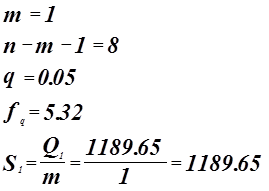
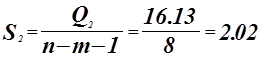
Критерий Фишера.
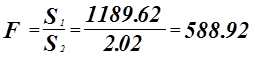
отсюда линия регрессии адекватна отраксает исходную информацию, гипотеза о равенстве мат. Ожиданий отвергается.
Проверка адекватности модели по коэффициенту детерминации или множественная корреляция.
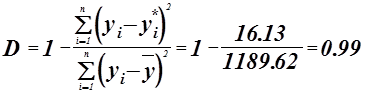
регрессионная модель адекватна
Коэффициент множественной корреляции:
Таблица 3
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 1.35 | 1.09 | 6.46 | 3.15 | 5.80 | 7.2 | 8.07 | 8.12 | 8.97 | 10.66 |
Приведем квадратное уравнение к линейной форме:
;
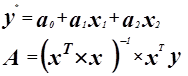
Запишем матрицу X.
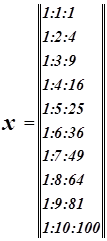
Составим матрицу Фишера.
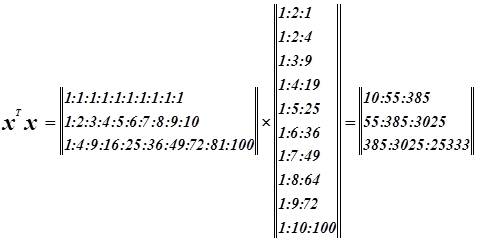
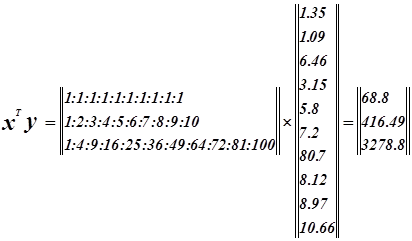
Система нормальных уравнений.
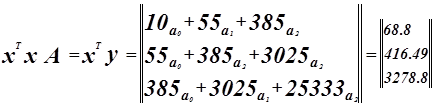
Решим ее методом Гаусса.
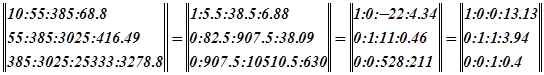
Уравнение регрессии имеет вид:
Оценка значимости коэффициентов регрессии.
Для проверки нулевой гипотезы используем критерий Стьюдента.
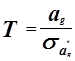
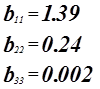
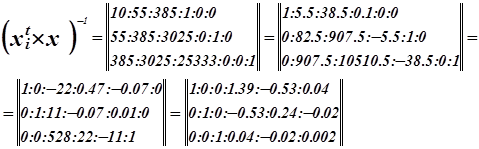
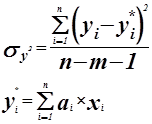
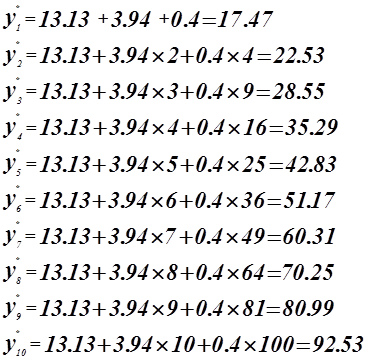
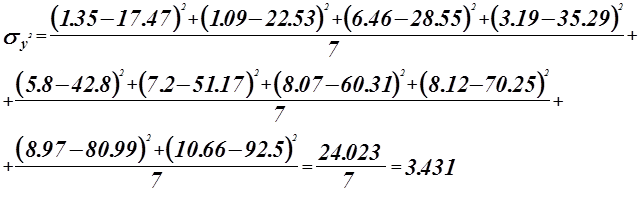
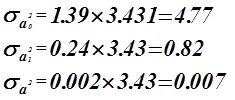
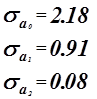
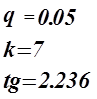
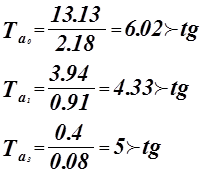
Коэффициенты 
значимые коэффициенты.
Проверка адекватности модели по критерию Фишера.
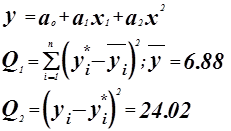
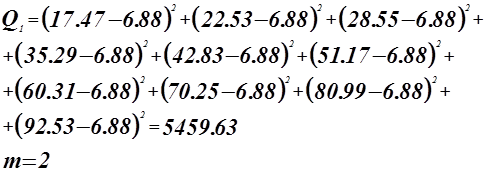
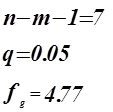
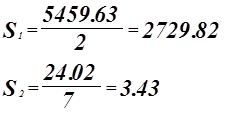
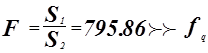гипотеза о равенстве математического ожидания отвергается.
Проверка адекватности модели по коэффициенту детерминации или множественной корреляции.
Коэффициент детерминации :
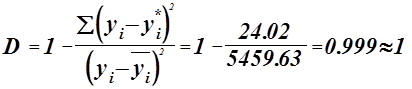
- регрессионная модель адекватна.
Коэффициент множественной корреляции 
Таблица 4
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 0,75 | 1,87 | 2,99 | 4,11 | 5,23 | 6,35 | 7,47 | 8,59 | 9,71 | 10,83 |
График 2
Таблица 5
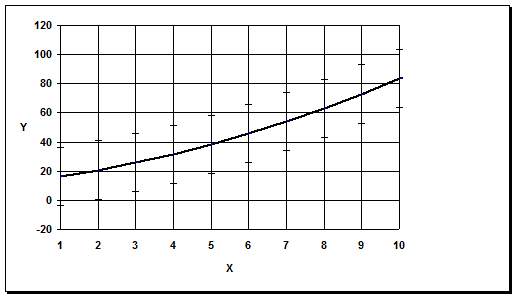
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 16.57 | 20.81 | 25.85 | 31.69 | 38.3 | 45.8 | 54 | 63.05 | 72.9 | 83.53 |
График 3
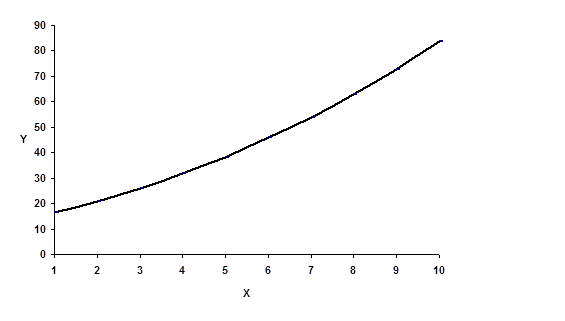
Использование регрессионной модели
для прогнозирования изменения показателя
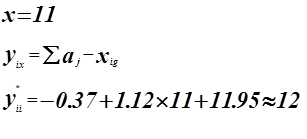
Оценка точности прогноза.
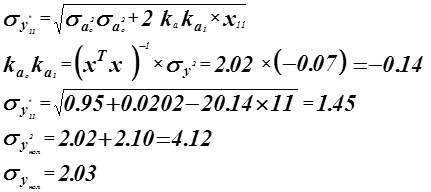
Построим доверительный интервал для заданного уровня надежности.
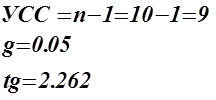
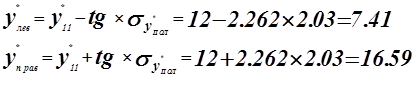
С вероятностью 0,05 этот интервал покрывает истинное значение прогноза
График 4
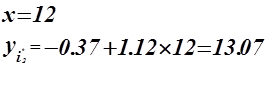
Оценка точности периода.
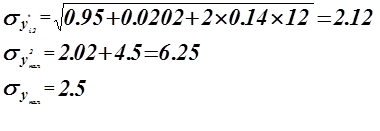
Построим доверительный интервал.
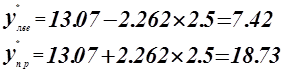
График 5
