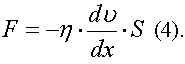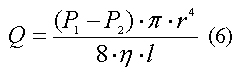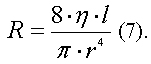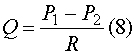| Скачать .docx | Скачать .pdf |
Реферат: Основы гидродинамики и гемодинамики
Гидродинамика - раздел физики, в котором на основе законов механики изучают движение жидкостей.
Гемодинамика изучает движение крови в кровеносной системе. Рассмотрим некоторые принципы гидродинамики.
Описание потока жидкости
Для описания течения жидкости необходимо рассмотреть движение небольшого ее объема. Линии, вдоль которых перемещаются частицы жидкости, называются линиями тока. Если каждая последующая частица жидкости проходит через данную точку, следуя по тому же пути, что и предыдущая частица жидкости, течение жидкости называется стационарным. Линии тока при стационарном течении жидкости отображают направление течения, которое может быть прямым или изогнутым. Касательная, проведенная в любой точке к линиям тока, указывает направление вектора скорости в данной точке.
Уравнение неразрывности
Рассмотрим движение несжимаемой жидкости через трубку переменного сечения. Если некоторый объем жидкости поступает в один конец трубки, то равный ему объем должен выйти через другой конец трубки.
Основным показателем течения жидкости в трубке является Q – объемная скорость течения жидкости - объем жидкости (V), перемещающейся за единицу времени через поперечное сечение трубки. Если объемная скорость жидкости, которая поступает через один конец трубки, составляет Q1, то объемная скорость жидкости, вытекающей из другого конца трубки, будет Q2, и она будет равна Q1. Этот принцип называется уравнением неразрывности. Таким образом, уравнение неразрывности можно записать: Q1 = Q2 (1).
Объемная скорость жидкости равна произведению линейной скорости жидкости ν(м/с) на площадь поперечного сечения трубки S: Q = v*S (2)
Для трубки с переменным поперечным сечением (S1, S2 и т.д.) имеем другую форму уравнения неразрывности: v1S1 = v2S2 = ... = vnSn (3).
Таким образом, произведение линейной скорости движения жидкости на площадь поперечного сечения одинаково во всех сечениях. Отсюда, если уменьшается S, то v при этом увеличивается, и наоборот.
Обычно линейная скорость течения не одинакова в каждой точке поперечного сечения. Уравнение неразрывности отражает среднюю скорость течения.
Вязкость
Вязкость - свойство жидкостей, обусловленное движением частиц жидкости относительно друг друга, что обуславливает возникновение сопротивления течению жидкости в целом. Вязкость возникает из-за внутреннего трения между молекулами жидкости. Такое трение обуславливает возникновение различия скоростей движения частиц в потоке жидкости.
Обратной величиной вязкости является текучесть. Различные жидкости отличаются по вязкости. Например, вязкость нефти больше, чем вязкость воды.
Вязкость является основным показателем в определении сил, которые преодолевают жидкости при перемещении в трубках и сосудах. Вязкость крови существенно влияет на ток крови в сердечно-сосудистой системе.
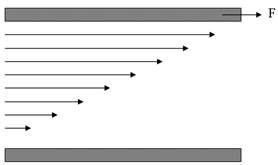 Рис. 1. Профиль векторов скоростей при ламинарном течении жидкости между двумя листами металла
Рис. 1. Профиль векторов скоростей при ламинарном течении жидкости между двумя листами металла
Понятие вязкости было предложено Ньютоном. Представим простой эксперимент, показанный на Рис. 1. Между двумя плоскими металлическими пластинами поместили тонкий слой жидкости. Нижняя пластина установлена неподвижно, а верхняя пластина под действием определенной силы перемещается с постоянной скоростью. Эта сила необходима для преодоления вязких свойств жидкости. Она должна иметь большие значения для более вязкой жидкости, чем для менее вязкой жидкости.
Если верхняя пластина перемещается, жидкость приходит в так называемое ламинарное движение. Каждый слой жидкости движется с некоторой скоростью ν. Каждый слой оказывает силовое действие на нижние пластины и испытывает действие равной силы в обратном направлении. В результате, скорости разных слоев жидкости оказываются не одинаковыми. Профиль векторов скоростей разных слоев жидкости показан на Рис. 1. Так формируется градиент скорости dν/dx.
Ньютон доказал, что сила внутреннего трения F пропорциональна площади соприкасающихся слоев жидкости S и градиенту скорости dν/dx:
|
|
Константа прямой пропорциональности (η- ″эта″), называется абсолютной вязкостью жидкости (или динамической вязкостью). Она равна силе внутреннего трения, возникающей между двумя слоями общей площадью, равной единице, при градиенте скорости между ними, равном 1. Единицей измерения вязкости является [Н·с/м2]или [Па·с]. Величина вязкости зависит от природы жидкости и ее температуры. Вязкость жидкостей уменьшается с увеличением температуре и наоборот.
В некоторых случаях удобней применять относительную вязкость, а не абсолютную. Относительная вязкость жидкости - это абсолютная вязкость этой жидкости, деленная на вязкость воды.
Ньютоновские и неньютоновские жидкости
Жидкости, вязкость которых может быть описана уравнением Ньютона, называются ньютоновскими. Это гомогенные жидкости (вода, духи, растворы электролитов и т.п.) Существуют также более сложные разнородные жидкости, для описания которых уравнение Ньютона неадекватно. Вязкость таких жидкостей, которые называются неньютоновскими жидкостями, зависит от скорости течения (при высоких их значениях). Эта категория жидкостей включает суспензии, эмульсии и растворы макромолекул (например, белков). Длинные цепочки макромолекул в растворах могут запутываться друг с другом, и это переплетение препятствует их способности реагировать на изменения скорости течения растворителя. Величина вязкости неньютоновских жидкостей большая, чем у ньютоновских жидкостей.
Ламинарное и турбулентное течение
Течение жидкости, показанное на Рис. 1, называется ламинарным. Слой жидкости, контактирующий с подвижной металлической пластиной, имеет ту же скорость, что и эта пластина. Слой жидкости, расположенный ниже, перемещается немного медленнее, и скорость каждого последующего слоя немного меньше, чем предыдущего. При этом каждый слой жидкости скользит по другому, и разные слои не перемешиваются.
В ламинарном потоке каждая частица жидкости следует по пути своей предыдущей частицы. Скорость течения в любой точке жидкости остается постоянной. Линии тока не пересекаются между собой. Энергия, сообщаемая жидкости для поддержания ее течения, используется, главным образом, на преодоление вязких сил между слоями жидкости.
Другой тип течения называется турбулентным. Турбулентное течение неустойчиво. Послойный характер течения жидкости нарушается. В потоке образуются местные завихрения, частицы перемещаются не только параллельно, но и перпендикулярно оси трубки, непрерывно перемешиваясь. Линии тока становятся искривленными. Скорость частиц, пересекающих конкретную точку жидкости, не является постоянной по направлению и величине: она изменяется со временем. Описание турбулентного потока должно быть статистическим: с точки зрения средних величин. Для турбулентного течения необходима большая энергия, чем для ламинарного, поскольку при турбулентном течении существенно возрастает внутреннее трение между частицами жидкости.
Английский физик Рейнольдс исследовал условия, при которых течение является ламинарным или турбулентным. Переход из ламинарного течения в турбулентное зависит от значения безразмерной величины, называемой числом Рейнольдса. Число Рейнольдса для жидкости, текущей в цилиндрической трубке определяется уравнением: Re = vDρ/η (5),
где v - средняя скорость потока, D - диаметр трубки, η - вязкость, и ρ - плотность жидкости.
Критическая величина числа Рейнольдса для цилиндрических трубок, при котором ламинарное течение становится турбулентным - 2000 - 2400.
Критическая скорость - скорость жидкости, при превышении которой ламинарное течение переходит в турбулентное. Течение крови в сосудах является ламинарным (за исключением аорты). В аорте наблюдается турбулентное течение крови во время физической работы, которая приводит к существенному увеличению скорости течения крои. Поток крови также может стать турбулентным в артериях при уменьшении площади их поперечного сечения вследствие патологических процессов. Причиной этого феномена является повышение скорости течения крови.
Закон Пуазейля
Закон Пуазейля представляет собой формулу для объемной скорости течения жидкости. Он был открыт экспериментально французским физиологом Пуазейлем, который исследовал течение крови в кровеносных сосудах. Закон Пуазейля часто называют главным законом гидродинамики.
Закон Пуазейля связывает объемную скорость течения жидкости с разностью давления в начале и конце трубки как движущей силой потока, вязкостью жидкости, радиусом и длиной трубки. Закон Пуазейля используют в случае, если течение жидкости ламинарное. Формула закона Пуазейля:
|
|
где Q - объемная скорость жидкости (м3/с), (P1 - P2) - различие давления через концы трубки (Па), r - внутренний радиус трубки (м), l - длина трубки (м), η - вязкость жидкости (Па с).
Закон Пуазейля показывает, что величина Q пропорциональна разнице давления P1 - P2 в начале и конце трубки. Если P1 равняется P2, поток жидкости прекращается. Формула закона Пуазейля также показывает, что высокая вязкость жидкости приводит к снижению объемной скорости течения жидкости. Оно также показывает, что объемная скорость жидкости чрезвычайно зависима от радиуса трубки. Это подразумевает, что умеренные изменения радиуса кровеносных сосудов могут обеспечивать большие различия объемной скорости жидкости, протекающей через сосуд.
Формула закона Пуазейля упрощается и становится более универсальной при введении вспомогательной величины - гидродинамического сопротивления R, которое для цилиндрической трубки может быть определено по формуле:
|
|
Закон Пуазейля, таким образом, показывает, что объемная скорость жидкости прямо пропорциональна разнице давления в начале и конце трубки и обратно пропорциональна гидродинамическому сопротивлению:
|
|
Вязкость крови
Кровь является взвесью клеток крови в жидкости сложного состава, называемой плазмой. Различают красные клетки крови (эритроциты), белые клетки крови (лейкоциты) и тромбоциты. Плазма - водный раствор электролитов, белков, питательных веществ, продуктов метаболизма и т.п. Объем крови в организме составляет почти 7% объема человеческого тела. Эритроциты занимают около 45 % объема крови, а другие клетки крови - менее чем 1%. Относительный объем клеток крови и плазмы определяют с помощью прибора гематокрита. Это же название используют для определения результатов анализа.
Кровь является более плотной и вязкой, чем вода. В среднем относительная вязкость крови составляет почти 4,5 (3,5-5,4). Относительная вязкость плазмы - 2,2 (1,9 - 2,6). Вязкость крови измеряется в лаборатории с помощью специального прибора - медицинского вискозиметра. Кровь является неньютоновской жидкостью. Но при такой скорости течения, которая поддерживается в сосудах кровеносной системы, вязкие свойства крови можно рассматривать, как для ньютоновских жидкостей.
Вязкость крови зависит, главным образом, от концентрации эритроцитов и меньше - от концентрации белков плазмы. Она зависит также от скорости течения крови. Если скорость течения крови уменьшается, эритроциты собираются в специфические скопления, так называемые ″монетные столбики. Это приводит к повышению вязкости крови. Такой феномен может наблюдаться в мелких кровеносных сосудах, где скорость течения крови небольшая.
Однако существует физиологический механизм, который способствует уменьшению вязкости крови в небольших сосудах, называемый эффектом Фареуса-Линдквиста. Этот эффект объясняется ориентацией эритроцитов вдоль оси сосуда. Эритроциты, формируя цилиндрический осевой ток, скользят по слою окружающей их плазмы крови.
Структура и некоторые биофизические свойства сердечно- сосудистой системы
Сердечно-сосудистая система состоит из сердца и разветвленной замкнутой системы кровеносных сосудов, которые перемещают кровь во все части тела и в сердце. Сосудистая система состоит из системной циркуляции и легочной циркуляции. Кровеносные сосуды включают артерии, капилляры и вены. По артериям кровь поступает в органы и ткани. Через вены перемещается обратный поток крови. Каждая большая артерия, начинающая с аорты, ветвится, формируя меньшие артерии, которые, в свою очередь, разветвляются дальше. Наименьшие артерии называются артериолами. Кровь, в конце концов, достигает капилляров, где происходит обмен веществ с окружающими тканями. Затем капилляры собираются в венулы и вены, которые собираются в полые вены, откуда кровь из тканей поступает в сердце.
Основные параметры циркуляции крови
В клинике наиболее часто исследуют давление и скорость течения крови.
Давление крови в артериях колеблется от максимального во время сокращения сердца (систолы) до минимального во время расслабления (диастолы). При каждом сердцебиении давление крови поднимается до систолического уровня, а между ударами падает до диастолического уровня. Поэтому артериальное давление определяют как максимальное/минимальное значение (систолическое/диастолическое). Обычно его измеряют в миллиметрах ртутного столба. Среднее значение артериального давления для здоровых взрослых людей в состоянии покоя составляет 120/60 мм.рт.ст.
Сфигмоманометр – наиболее часто используемый прибор для измерения давления крови. Сфигмоманометр состоит из надувной манжеты, в которую с помощью резиновой груши нагнетают воздух, увеличивая в ней давление. Эта система связана с манометром, по шкале которого определяют артериальное давление пациента. Манжету фиксируют на плече, фонендоскоп устанавливают в локтевом сгибе.
Давление в манжете увеличивают до тех пор, пока в артерии не прекратиться ток крови. Затем давление в манжете медленно уменьшают. Когда оно достигнет максимального (систолического) значения, артерия частично открывается. Поскольку сечение артерии в этот момент меньше, чем обычно, в ней создается высокая скорость течения крови, и это течение является турбулентным. Поэтому фонендоскопом можно услышать звуки - тоны Kороткова.
Если продолжать уменьшать давление в манжете, артерия в течение некоторого периода остается еще достаточно сжатой, по сравнению с нормальным состоянием. Следовательно, тоны Короткова слышны до тех пор, пока давление в манжете не достигнет минимального (диастолического) значения. В этот момент кровь начинает свободно проходить через артерию. В артерии восстанавливается ламинарное течение крови, и тоны Короткова исчезают. Таким образом, измеряют максимальное и минимальное давление крови.
Скорость течения крови измеряют, используя эффект эходоплерографии. Как давление крови, так и скорость ее течения являются важными диагностическими показателями.
Давление и скорость течения крови в разных отделах кровеносной системы
Самое высокое давление в кровеносной системе в сердце. По закону Пуазейля: P1 - P2 = QR. Допустим, что P1 – давление крови в аорте и P2 - давление крови в полой вене, которое составляет около нуля мм.рт.ст. Следовательно, давление крови в аорте определяется двумя переменными.
(1) Первая из них - объемная скорость жидкости (Q) в аорте, величина которой зависит от частоты, мощности сердечных сокращений и объема в кровеносной системе.
(2) Вторая – общее сопротивление (R) кровеносной системы.
Давление крови уменьшается с расстоянием от сердца из-за трения в кровеносных сосудах. Давление крови является мерой энергии, которую сообщает крови сердце. Эта энергия рассеивается при преодолении сопротивления кровеносных сосудов.
Гидродинамическое сопротивление разных частей кровеносной системы не одинаково. Сопротивление аорты и больших артерий составляет только около 19% общей величины сопротивления в системе. Самая большая доля сопротивления принадлежит артериолам (50%) и капиллярам (25%)). Таким образом, на сосуды, длина которых составляет не несколько миллиметров, приходится более половины общего сопротивления циркуляторного русла. Сопротивление вены составляет около 7% общей величины сопротивления в кровеносной системе.
Величина гидродинамического сопротивления определяет падение давления крови по ходу сосудистого русла (Рис. 2). Среднее давление крови немного снижается в артериях (по отношению к давлению в аорте), но резкое его падение наблюдается в артериолах и капиллярах. Сопротивление артериол является одним из основных факторов, определяющих величину артериального давления. Изменения давления крови в венах очень небольшие.
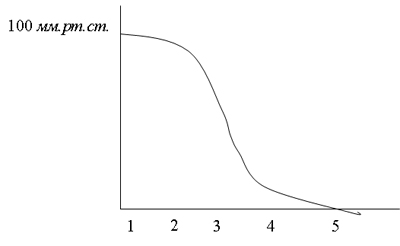 Рис. 2. Среднее давление крови в разных отделах кровеносной системы. 1. Аорта. 2. Артерии. 3. Артериолы. 4.Капилляры. 5. Вены.
Рис. 2. Среднее давление крови в разных отделах кровеносной системы. 1. Аорта. 2. Артерии. 3. Артериолы. 4.Капилляры. 5. Вены.
Средние величины давления крови (мм.рт.ст.): 100 - в небольших артериях, 95 - при переходя из артерий в артериолы, 35-70 - при поступлении крови из артериол в капилляры, 20-35 – в больших венах, 10 и менее – в мелких венах.
Скорость течения крови также значительно различается в разных отделах кровеносной системы (Рис. 3). Средняя величина скорости течения крови определяется уравнением неразрывности: она обратно пропорциональна общей площади поперечного сечения параллельно соединенных сосудов. Например, площадь поперечного сечения аорты составляет около 3,5-4,5, тогда как суммарная площадь поперечного сечения капилляров - в 600 раз большая. Поэтому средняя скорость крови составляет 0,2 в аорте и только 0,0003 в капиллярах. Небольшая скорость течения крови в капиллярах имеет большое значение для обмена веществ между кровью и окружающими тканями.
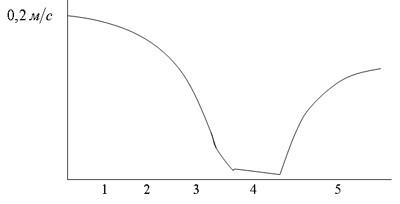 Рис.3. Средняя скорость течения крови в разных отделах кровеносной системы.
Рис.3. Средняя скорость течения крови в разных отделах кровеносной системы.
1. Аорта. 2. Артерии. 3. Артериолы. 4. Капилляры. 5. Вены.