| Скачать .pptx |
Презентация: Основные понятия высшей математики
Высшая математика
(учебный курс)
Составитель
доцент кафедры математики и моделирования ВГУЭС
Шуман Галина Ивановна
Оглавление
- Элементы линейной алгебры
- Дифференциальное и интегральное исчисление функции одной переменной
- Функция нескольких переменных
- Обыкновенные дифференциальные уравнения
- Комбинаторные формулы
- Статистическое определение вероятности.
- Формула полной вероятности.
- Асимптотические формулы для формулы Бернулли.
- Дискретные случайные величины.
- Биномиальный закон распределения.
- Непрерывные случайные величины.
- Правило 3-х s (трех “сигм”).
- Распределение c2 .
- Математическая статистика.
- Интервальные оценки.
- Задачи статистической проверки гипотез.
Элементы линейной алгебры
Оглавление раздела
§ 1. Системы линейных уравнений
§ 2. Метод Гаусса решения систем линейных
уравнений
§ 3. Элементы теории матриц
§ 4. Определители
§ 5. Вычисление обратной матрицы
§ 6. Правило Крамера решения квадратных систем линейных равнений
§ 1. Системы линейных уравнений
Систему m линейных уравнений с n неизвестными будем записывать в следующем виде:
§ 1. Системы линейных уравнений
Решением системы будем называть упорядоченный набор чисел x 1 , x 2 , … , xn , обращающий каждое уравнение системы в верное равенство.
Решить систему — значит найти все ее решения или доказать, что ни одного решения нет.
Система, имеющая решение, называется совместной .
§ 1. Системы линейных уравнений
Если система имеет только одно решение, то она называется определенной .
Система, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной ).
Если система не имеет решений, то она называется несовместной .
§ 1. Системы линейных уравнений
Система, у которой все свободные члены равны нулю (b 1 = b 2 =…= bn = 0), называется однородной .
Однородная система всегда совместна, так как набор из n нулей удовлетворяет любому уравнению такой системы.
Если число уравнений системы совпадает с числом неизвестных (m=n ), то система называется квадратной .
§ 1. Системы линейных уравнений
Две системы, множества решений которых совпадают, называются
эквивалентными или равносильными .
Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием .
§ 2. Метод Гаусса решения систем линейных уравнений
Рассмотрим квадратную систему:
§ 2. Метод Гаусса решения систем линейных уравнений
Проведем следующие преобразования системы:
1) поскольку a 11 ≠ 0 , первое уравнение оставим без изменений;
2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;
3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;
4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.
§ 2. Метод Гаусса решения систем линейных уравнений
Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x 1 (это и являлось целью преобразований 1 – 4):
§ 2. Метод Гаусса решения систем линейных уравнений
Можно доказать, что
замена любого уравнения системы новым, получающимся прибавлением к данному уравнению любого другого уравнения системы, умноженного на любое число, является эквивалентным преобразованием системы.
§ 2. Метод Гаусса решения систем линейных уравнений
Исходную систему можно представить в виде таблицы:
§ 2. Метод Гаусса решения систем линейных уравнений
Прямоугольную таблицу, состоящую из p строк и q столбцов, будем называть матрицей размера p × q :
§ 2. Метод Гаусса решения систем линейных уравнений
Числа aij называются элементами матрицы. Первый индекс фиксирует номер строки, а второй – номер столбца, в которых стоит данный элемент. Если p = q , то есть число столбцов матрицы равно числу строк, то матрица называется квадратной . Элементы aii образуют главную диагональ матрицы.
Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы , которую иногда называют просто матрицей системы .
§ 2. Метод Гаусса решения систем линейных уравнений
Системе (2) соответствует расширенная матрица:
§ 2. Метод Гаусса решения систем линейных уравнений
Преобразуем эту матрицу следующим образом :
1) первые две строки оставим без изменения, поскольку элемент a 22 не равен нулю;
2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;
3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.
§ 2. Метод Гаусса решения систем линейных уравнений
В результате получится матрица, соответствующая системе, у которой неизвестная x 1 исключена из всех уравнений, кроме первого, а неизвестная x 2 — из всех уравнений кроме первого и второго:
§ 2. Метод Гаусса решения систем линейных уравнений
Теперь исключим неизвестную x
3
из четвертого уравнения.
Для этого последнюю матрицу преобразуем так:
1) первые три строки оставим без изменения, так как a 33 ≠ 0 ;
2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой:
§ 2. Метод Гаусса решения систем линейных уравнений
Полученная матрица соответствует системе:
§ 2. Метод Гаусса решения систем линейных уравнений
Из последнего уравнения этой системы получаем x 4 = 2. Подставив это значение в третье уравнение, получим x 3 = 3. Теперь из второго уравнения следует, что x 2 = 1, а из первого — x 1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x 4 , затем x 3 и т. д.).
Назовем элементарными преобразованиями матрицы следующие преобразования:
1) перемена местами двух строк;
2) умножение строки на число, отличное от нуля;
3) замена строки матрицы суммой этой строки с любой другой строкой, умноженной на некоторое число.
§ 2. Метод Гаусса решения систем линейных уравнений
Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей .
Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна .
§ 2. Метод Гаусса решения систем линейных уравнений
Если матрицу A можно разделить вертикальной чертой на две матрицы: стоящую слева треугольную матрицу размера m и стоящую справа прямоугольную матрицу, то матрицу A назовем трапециевидной или трапецеидальной .
Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к трапецеидальному виду и при этом система не получается противоречивой, то система совместна и является неопределенной, то есть имеет бесконечно много решений .
§ 2. Метод Гаусса решения систем линейных уравнений
Те переменные, коэффициенты при которых стоят на главной диагонали трапецеидальной матрицы (это значит, что эти коэффициенты отличны от нуля), называются базисными .
Остальные неизвестные называются свободными .
Если свободным неизвестным приданы конкретные числовые значения и через них выражены базисные неизвестные, то полученное решение называется частным решением .
Если свободные неизвестные выражены через параметры, то получается решение, которое называется общим решением .
§ 2. Метод Гаусса решения систем линейных уравнений
Если всем свободным неизвестным приданы нулевые значения, то полученное решение называется базисным .
Если получены два различных набора базисных неизвестных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число неизвестных, называемое рангом системы .
§ 3. Элементы теории матриц
Две матрицы одинаковой размерности p ´ q называются равными , если в них одинаковые места заняты равными числами (на пересечении i -й строки и j- го столбца в одной и в другой матрице стоит одно и то же число; i =1, 2, ..., p ; j =1, 2, ..., q ).
Пусть A = (aij ) – некоторая матрица и a – произвольное число, тогда a A = (a aij ), то есть при умножении матрицы A на число a все числа, составляющие матрицу A, умножаются на число a .
§ 3. Элементы теории матриц
Пусть A и B – матрицы одинаковой размерности A = (aij ), B = (bij ), тогда их сумма A + B – матрица C = (cij ) той же размерности, определяемая из формулы cij = aij + bij , то есть при сложении двух матриц попарно складываются одинаково расположенные в них числа .
Матрицу A можно умножить на матрицу B, то есть найти матрицу C = AB, если число столбцов n матрицы A равно числу строк матрицы B, при этом матрица C будет иметь столько строк, сколько строк у матрицы A и столько столбцов, сколько столбцов у матрицы B .
§ 3. Элементы теории матриц
Каждый элемент матрицы C определяется формулой:
§ 3. Элементы теории матриц
§ 3. Элементы теории матриц
§ 4. Определители
§ 4. Определители
§ 4. Определители
§ 4. Определители
§ 4. Определители
§ 4. Определители
§ 4. Определители
§ 4. Определители
§ 5. Вычисление обратной матрицы
§ 5. Вычисление обратной матрицы
§ 6. Правило Крамера решения квадратных систем линейных равнений
Дифференциальное и интегральное исчисление функции одной переменной
Оглавление раздела
§ 1. Основные понятия
§ 2. Предел и непрерывность функции
§ 3.Производная
§ 4 . Дифференциал функции
§ 5. Производные высших порядков
§ 6. Формула Лагранжа
§ 7. Необходимые и достаточные условия экстремума функции
§ 8. Выпуклость и вогнутость функции
§ 9. Неопределенный интеграл
§ 10. Замена переменной в неопределенном интеграле
§ 11. Формула интегрирования по частям
§ 12. Определенный интеграл
§ 13. Определенный интеграл как функция верхнего предела
§ 14. Несобственные интегралы с бесконечными пределами
Пусть D — некоторое множество чисел. Если задан закон, по которому каждому числу x из множества D ставится в соответствие единственное определенное число y , то будем говорить, что на множестве D задана функция, которую назовём f . Число y — это значение функции f в точке x , что обозначается формулой y = f(x) .
Число x называется аргументом функции, множество D — областью определения функции, а все значения y образуют множество E , которое называется множеством значений или областью изменения функции.
§1. Основные понятия
Функция f называется возрастающей ( убывающей ) на множестве G , если для любых чисел х1 и х2 из множества G , таких что x1 < x2 , выполняется условие f(x1 ) < f(x2 ) (f(x1 ) > f(x2 )).
Пусть e — некоторое положительное число. e -окрестностью точки x0 называется множество всех точек x , принадлежащих промежутку (x0 ‑ e , x0 + e ) , кроме самой точки x0 . Принадлежность точки x e ‑ окрестности точки можно выразить с помощью двойного неравенства
0 < ê x – x0 ç < e .
Число e называется радиусом окрестности .
§ 2. Предел и непрерывность функции
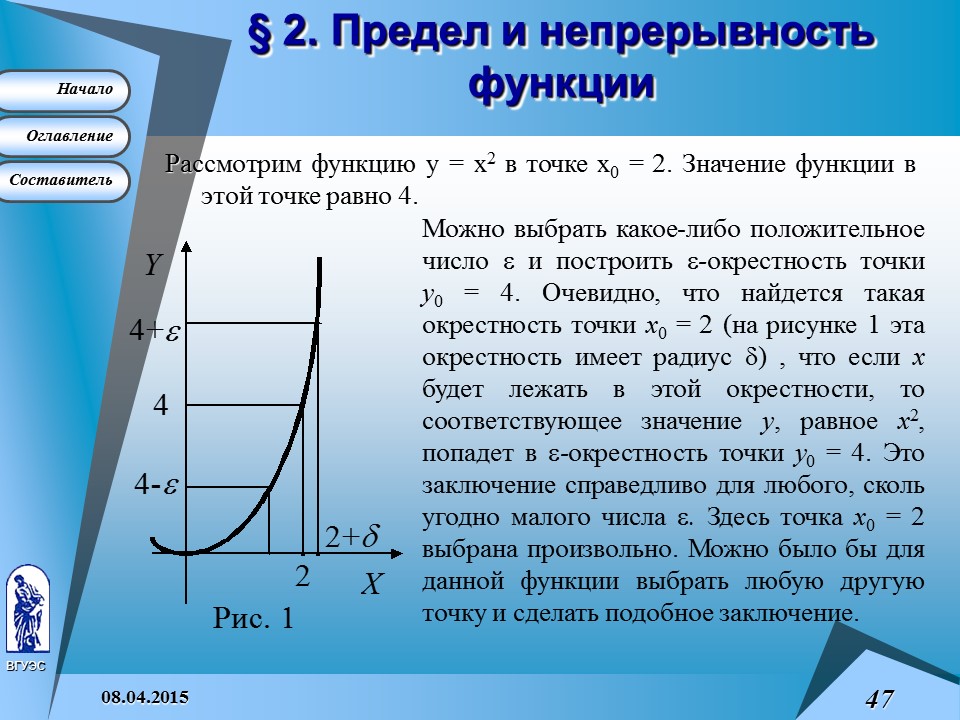
Рассмотрим функцию y = x2 в точке x0 = 2. Значение функции в этой точке равно 4.
§ 2. Предел и непрерывность функции
Рассмотрим функцию . Эта функция не
определена в точке x 0 = 2. При x 0 ¹ 2 её можно преобразовать:
Введем понятие предела функции :
Число A называется пределом функции y = f (x ) в точке x 0 (иногда говорят, при x , стремящемся к x 0 ), если для любого положительного числа e можно найти такое положительное число d, что для всех x из d- окрестности точки x 0 соответствующие значения y попадают в e- окрестность точки y = A .
§ 2. Предел и непрерывность функции
Можно сформулировать определение предела функции по-другому :
Число A называется пределом функции y = f (x ) в точке x0 , если для любого положительного числа e можно найти такое положительное число d, что для всех x , удовлетворяющих условию 0 < ê x – x 0 ê < d , выполняется условие ê y – A ê < e .
§ 2. Предел и непрерывность функции
Тот факт, что A есть предел функции y = f (x ) в точке x = x 0 , записывается формулой:
Рассмотрим функцию .
Очевидно, что если x > 0 , то y = 2x ; если x < 0 ,
то y = –2x ; при x = 0 функция не определена.
§ 2. Предел и непрерывность функции
График функции изображен на рисунке 3. Легко убедиться в том, что, согласно приведенному выше определению предела, эта функция в точке x = 0 предела не имеет.
§ 2. Предел и непрерывность функции
Функция y = f (x ) называется непрерывной в точке x = x 0 , если она определена в этой точке и ее значение f (x 0 ) равно пределу функции в этой точке:
Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке .
§ 2. Предел и непрерывность функции
Приведем свойства предела функции.
1. Функция не может иметь в одной точке два разных предела.
2. , если C — постоянная функция.
3. Если существует и C — постоянная
функция, то
§ 2. Предел и непрерывность функции
4. Если существуют и , то
существует , равный
а также существует ,
равный . Если при этом ,
то существует ,
равный .
§ 2. Предел и непрерывность функции
Число B называется пределом функции f (x ) в точке a
справа
(это записывается в виде формулы ),
если для любого положительного числа e найдется
положительное число d , такое что из условия
0 < x – a < d будет следовать ê B –f (x ) ê < e .
§ 2. Предел и непрерывность функции
Число С называется пределом функции f (x ) в точке b
слева
(это записывается в виде формулы ),
если для любого положительного числа e найдется
положительное число d такое, что из условия
0 < b – x < d будет следовать ê C – f (x ) ê < e .
§ 2. Предел и непрерывность функции
Функция f (x ) называется непрерывной в точке a справа (непрерывной в точке b слева ), если
Функция называется непрерывной на замкнутом промежутке [a , b ], если она непрерывна на открытом промежутке (a , b ), непрерывна справа в точке a и непрерывна слева в точке b .
§ 2. Предел и непрерывность функции
Для того, чтобы выполнялось равенство
,
необходимо и достаточно, чтобы
одновременно выполнялись два равенства:
§ 2. Предел и непрерывность функции
Число А называется пределом функции f ( x ) при х , стремящемся к бесконечности:
,
если для любого положительного числа e можно найти такое положительное число M (зависящее от e ), что для всех чисел х , превосходящих М , выполняется условие:
½ f ( x ) – A ½ < e .
§ 2. Предел и непрерывность функции
Число А называется пределом функции f ( x ) при х , стремящемся к минус бесконечности:
,
если для любого положительного числа e можно найти такое положительное число M (зависящее от e ), что для всех чисел х , превосходящих - М , выполняется условие:
½ f ( x ) – A ½ < e .
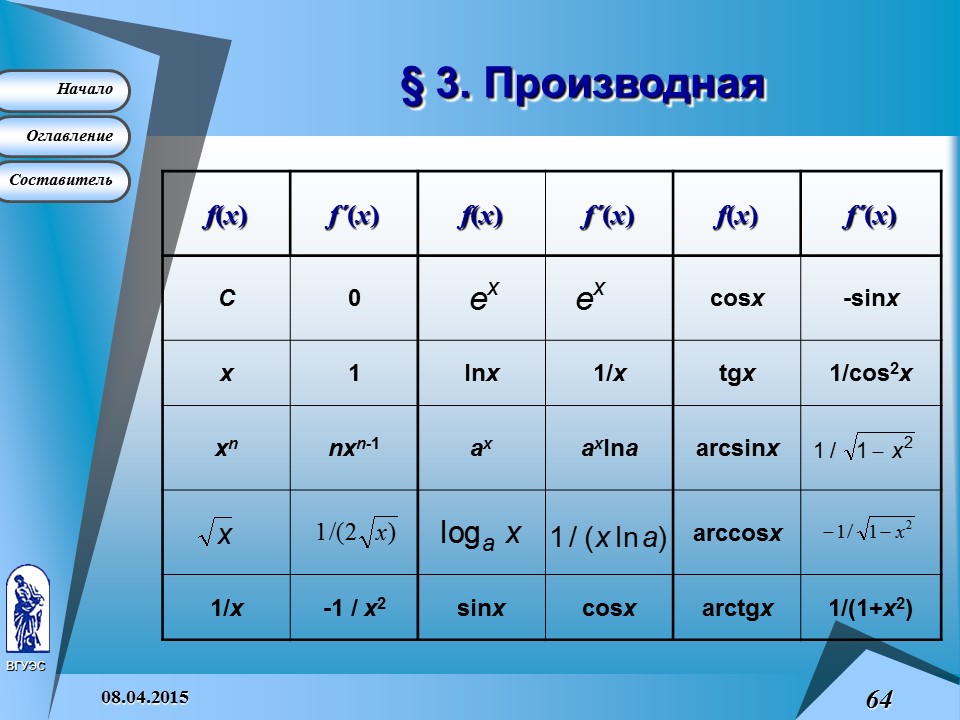
§ 3.Производная
Если существует предел отношения
(f (x + D x ) – f (x )) / D x
в точке D x = 0 , то он называется производной функции y = f (x ) в точке x и обозначается y ¢ или f ¢ (x ) :
§ 3.Производная
Нахождение производной функции y = f (x ) называется дифференцированием .
Если для любого числа x из открытого промежутка (a , b ) можно вычислить f ¢ (x ), то функция f (x ) называется дифференцируемой на промежутке (a , b ).
Геометрический смысл производной заключается в том, что производная функции f (x ) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.
Производная - это скорость изменения функции в точке x .
§ 3. Производная
§ 3. Производная
В любом курсе математического анализа доказывается теорема о производной сложной функции . Мы ограничимся лишь ее формулировкой.
Пусть функция g (x ) имеет производную в точке x , а функция f (z ) имеет производную в точке z = g (x ) . Тогда сложная функция F (x ) = f (g(x )) имеет в точке x производную F ¢ (x ) = f ¢ (z ) g ¢ (x ) .
§ 4 . Дифференциал функции
Главная, линейная относительно Dx , часть приращения функции y = f (x ) , равная f ¢ (x ) D x , называется дифференциалом и обозначается dy :
dy = f ¢ (x ) D x.
Производная функции f (x ) равна отношению дифференциала функции к дифференциалу аргумента x .
§ 5. Производные высших порядков
Может оказаться что функция f ¢ (x ) , называемая первой производной, тоже имеет производную (f ¢ (x )) ¢ . Эта производная называется второй производной функции f (x ) и обозначается f ¢¢ (x ) .
Если эта функция имеет производную, то эта производная называется третьей производной функции f (x ) и обозначается f ¢¢¢ (x ) .
Все производные, начиная со второй, называются производными высших порядков .
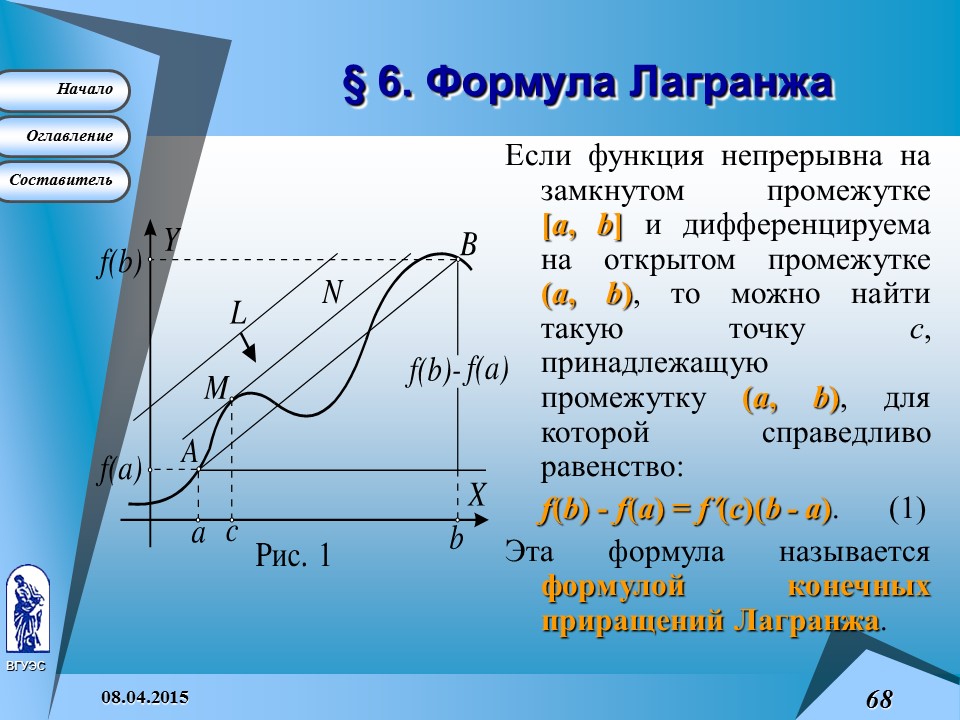
§ 6. Формула Лагранжа
Если функция непрерывна на замкнутом промежутке [a , b ] и дифференцируема на открытом промежутке (a , b ) , то можно найти такую точку c , принадлежащую промежутку (a , b ) , для которой справедливо равенство:
f (b ) - f (a ) = f ¢ (c )(b - a ) . (1)
Эта формула называется формулой конечных приращений Лагранжа .
§ 6. Формула Лагранжа
Сформулируем теорему о монотонности функции.
Если f ¢ (x ) > 0 на промежутке (a ;b ) , то на (a ;b ) функция f (x ) возрастает .
Если f ¢ (x ) < 0 на промежутке (a ;b ) , то на (a ;b ) функция f (x ) убывает .
§ 7. Необходимые и достаточные условия экстремума функции
Точка x 0 называется точкой минимума функции f (x ) ,
§ 7. Необходимые и достаточные условия экстремума функции
Точка x 0 называется точкой максимума функции f (x ) ,
§ 7. Необходимые и достаточные условия экстремума функции
Сформулируем теорему о необходимом условии экстремума функции:
Если в точке экстремума функция f (x ) имеет производную, то производная равна нулю .
§ 7. Необходимые и достаточные условия экстремума функции
Точка, в которой производная равна нулю, называется стационарной .
Точки области определения функции, в которых производная либо равна нулю, либо не существует, называются критическими .
§ 7. Необходимые и достаточные условия экстремума функции
Докажем теорему, которая называется достаточным условием экстремума .
Пусть функция f (x ) непрерывна в точке x 0 . Тогда:
1) если f ¢ (x ) < 0 на (a ;x 0 ) и f ¢ (x ) > 0 на (x 0 ;b ) , то точка x 0 – точка минимума функции f (x ) ;
2) если f ¢ (x ) > 0 на (a ;x 0 ) и f ¢ (x ) < 0 на (x 0 ;b ) , то точка x 0 – точка максимума функции f (x ) ;
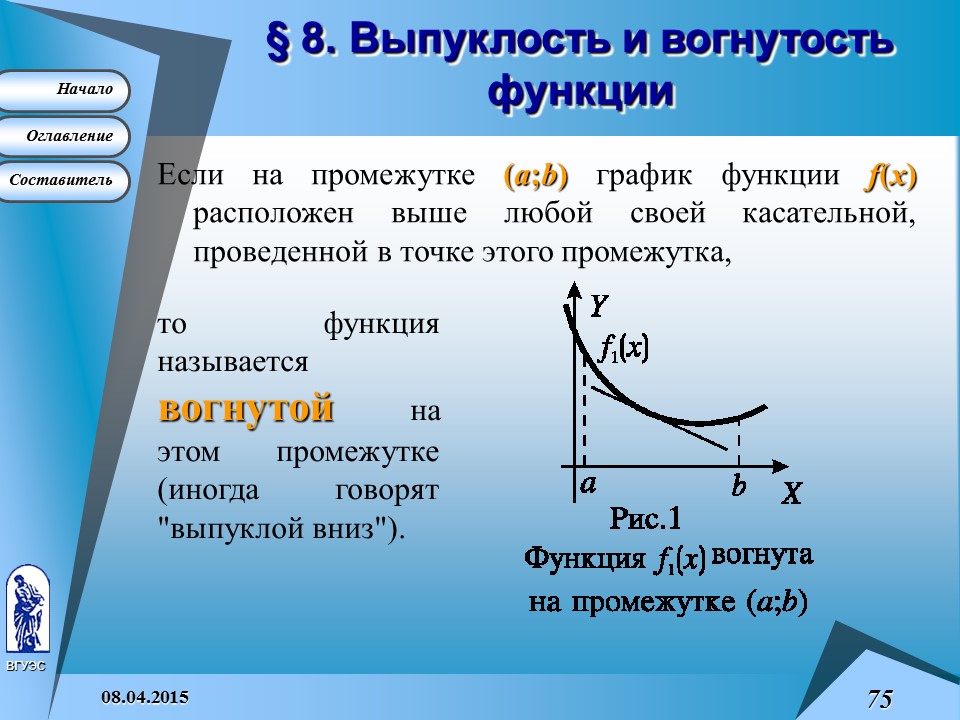
§ 8. Выпуклость и вогнутость функции
Если на промежутке (a ;b ) график функции f (x ) расположен выше любой своей касательной, проведенной в точке этого промежутка,
§ 8. Выпуклость и вогнутость функции
Если на промежутке (a ;b ) график функции f (x ) расположен ниже любой своей касательной, проведенной в точке этого промежутка,
§ 8. Выпуклость и вогнутость функции
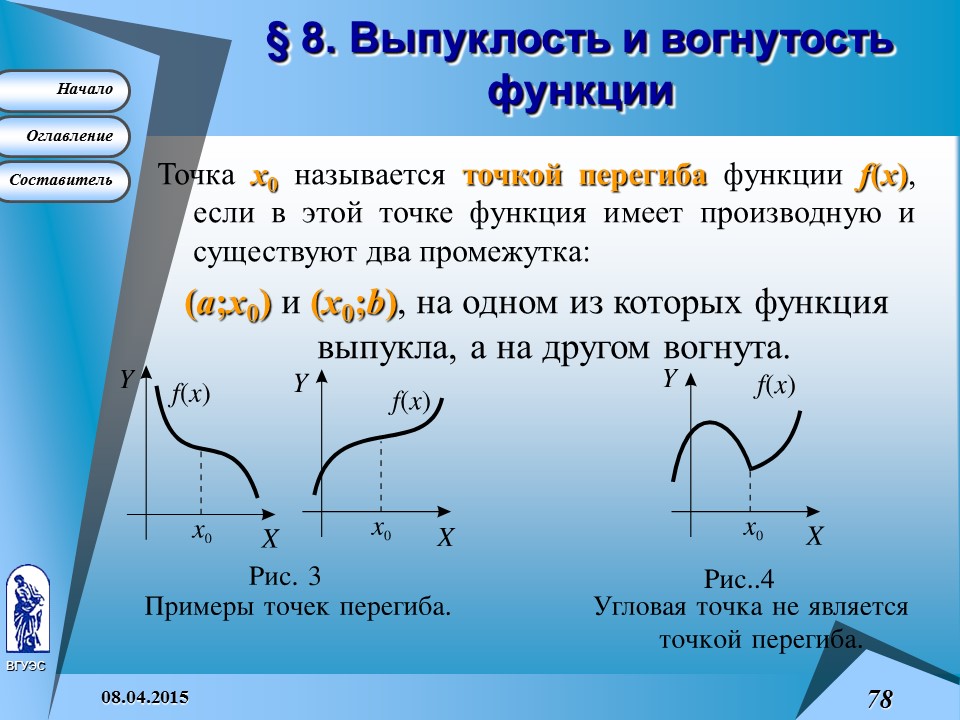
Точка x 0 называется точкой перегиба функции f (x ) , если в этой точке функция имеет производную и существуют два промежутка:
§ 8. Выпуклость и вогнутость функции
Точка x 0 называется точкой перегиба функции f (x ) , если в этой точке функция имеет производную и существуют два промежутка:
(a ;x 0 ) и (x 0 ;b ) , на одном из которых функция выпукла, а на другом вогнута.
§ 8. Выпуклость и вогнутость функции
Будем называть функцию возрастающей в точке x 0 , если она непрерывна в этой точке и возрастает в некоторой ее окрестности. Подобным образом можно определить функцию, убывающую в точке.
§ 8. Выпуклость и вогнутость функции
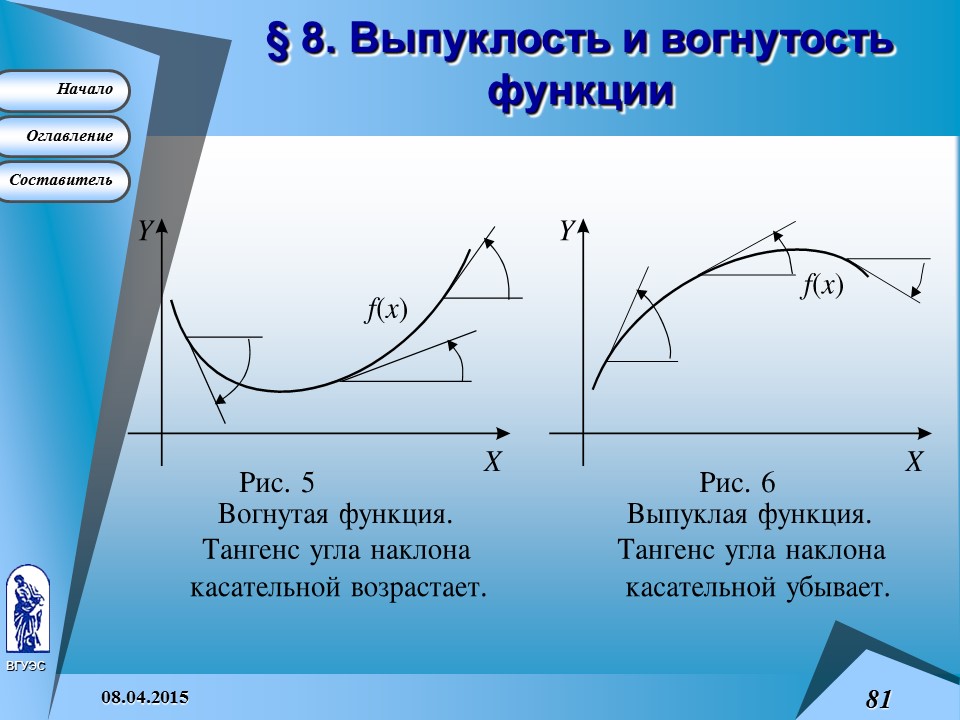
Если f ¢¢ (x ) > 0 на промежутке (a ;b ) , то на этом промежутке функция f (x ) вогнута .
Если f ¢¢ (x ) < 0 на промежутке (a ;b ) , то на этом промежутке функция f (x ) выпукла .
§ 8. Выпуклость и вогнутость функции
§ 9. Неопределенный интеграл
Функция F (x ) называется первообразной для функции f (x ) на промежутке (a ;b ) , если для всех x Î (a ;b ) выполняется равенство F ¢ (x ) = f (x ).
§ 9. Неопределенный интеграл
Теорема 1.
Если F (x ) – первообразная для f (x ) на (a ;b ), то F (x ) + C , где C – число, тоже первообразная для f (x ) на (a ;b ).
Доказательство.
(F + C) ¢ = F ¢ + C ¢ = f + 0 = f
§ 9. Неопределенный интеграл
Прежде чем рассмотреть теорему 2, докажем две вспомогательные теоремы.
Если функция g (x ) постоянна на (a ;b ) , то g ¢ (x ) = 0.
Если g ¢ (x ) = 0 при всех x Î (a ;b ) , то g (x ) = C на (a ;b ) .
§ 9. Неопределенный интеграл
Теорема 2.
Если F (x ) есть первообразная для f (x ) на промежутке (a ;b ) ,
а G (x ) – другая первообразная для f (x ) на (a ;b ) ,
то G = F + C , где C – число .
§ 9. Неопределенный интеграл
Множество всех первообразных для функции f (x ) на промежутке (a ;b ) называется неопределенным интегралом и обозначается ò f (x )dx .
Вычисление неопределенного интеграла от заданной функции называется интегрированием .
§ 10. Замена переменной в неопределенном интеграле
Если функция f (x ) непрерывна, а функция j (t ) имеет непрерывную производную j ¢ (t ) , то имеет место формула:
ò f ( j (t )) j ¢ (t ) dt = ò f(x) dx ,
где x = j (t ).
§ 11. Формула интегрирования по частям
Пусть u (x ) и v (x ) — дифференцируемые на некотором промежутке функции. Тогда
(uv ) ¢ = u ¢ v + v ¢ u
Отсюда следует
ò (uv ) ¢ dx = ò (u ¢ v + v ¢ u )dx = ò u ¢ v dx + ò v ¢ u dx
или
ò uv ¢ dx = uv – ò u ¢ v dx .
Отсюда следует формула, которая называется формулой интегрирования по частям :
ò u (x )dv (x ) = u (x ) v (x ) – ò v (x )du (x )
§ 12. Определенный интеграл
Определенным интегралом
от функции по промежутку [a ;b ] называется предел, к которому стремится интегральная сумма при этом процессе, если предел существует:
§ 12. Определенный интеграл
Число a называется нижним пределом интегрирования , а число b ¾ верхним пределом интегрирования .
На рисунке 2 криволинейная трапеция выделена штриховкой. Площадь S этой трапеции определяется формулой
§ 13. Определенный интеграл как функция верхнего предела
Пусть функция f (t ) определена и непрерывна на некотором промежутке, содержащем точку a . Тогда каждому числу x из этого промежутка можно поставить в соответствие число
,
определив тем самым на промежутке функцию I (x ) , которая называется определенным интегралом с переменным верхним пределом .
§ 13. Определенный интеграл как функция верхнего предела
Производная определенного интеграла по верхнему пределу в точке x равна значению подынтегральной функции в точке x .
§ 13. Определенный интеграл как функция верхнего предела
Формула Ньютона-Лейбница.
Здесь F (x) — любая первообразная функции f (x ).
§ 14. Несобственные интегралы с бесконечными пределами
Пусть функция y = f (x ) определена и непрерывна на полубесконечном промежутке [a ; ¥ ) , тогда несобственным интегралом с бесконечным пределом
называется ,
если предел существует .
§ 14. Несобственные интегралы с бесконечными пределами
Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится .
При существовании предела говорят, что несобственный интеграл сходится .
Функция нескольких переменных
Оглавление раздела
§1. Основные понятия
§2. Частные производные
§3. Дифференциал функции двух
переменных
§4. Производная по направлению
§5. Экстремум функции двух переменных
§6. Метод наименьших квадратов
§ 1. Основные понятия
Пусть имеется n +1 переменная x 1 , x 2 , ..., x n , y , которые связаны между собой так, что каждому набору числовых значений переменных x 1 , x 2 , ..., xn соответствует единственное значение переменной y .
Тогда говорят, что задана функция f от n переменных. Число y , поставленное в соответствие набору x 1 , x 2 , ..., xn называется значением функции f в точке (x 1 , x 2 , ..., xn ) , что записывается в виде формулы
y=f (x 1 ,x 2 , ..., xn ) или y =y (x 1 ,x 2 , ..., xn ) .
§ 1. Основные понятия
Будем говорить, что задана функция двух переменных, если любой паре чисел (x,y ) из некоторого множества D поставлено в соответствие единственное число, которое обозначается f (x,y ) и называется значением функции f в точке (x,y ) .
Множество D называется областью определения функции.
§ 1. Основные понятия
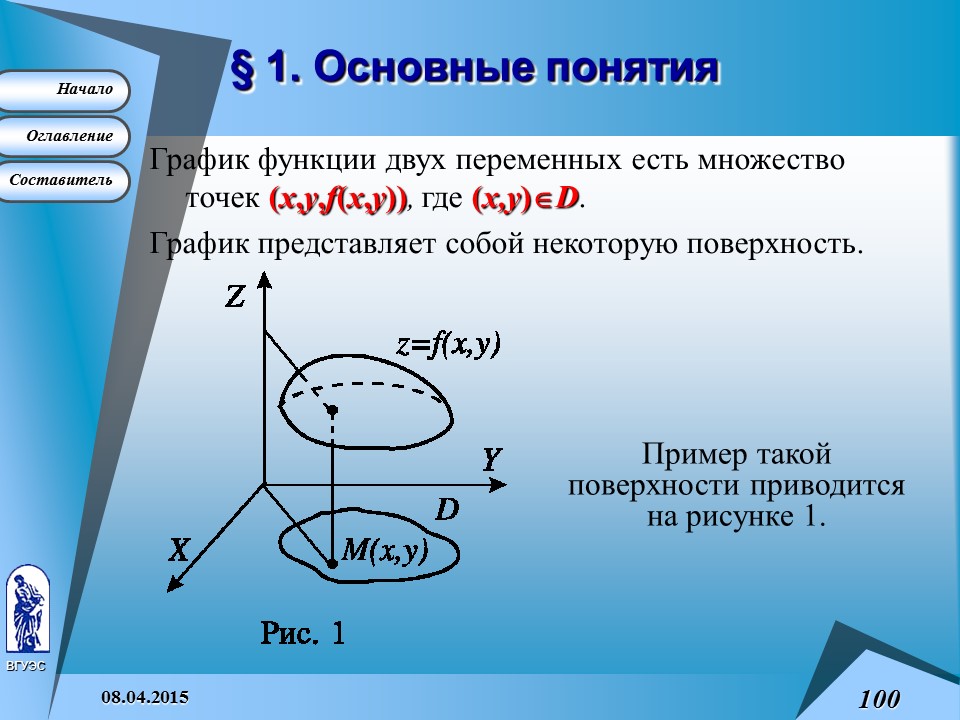
График функции двух переменных есть множество точек (x ,y ,f (x ,y )) , где (x,y ) Î D .
График представляет собой некоторую поверхность.
§ 1. Основные понятия
Пусть d ‑ некоторое положительное число.
d -окрестностью V d точки M 0 (x 0 ,y 0 ) называется множество всех точек, координаты x,y которых удовлетворяют неравенствам
§ 1. Основные понятия
Точка M 0 (x 0 ,y 0 ) называется точкой минимума функции z = f (x ,y ) , если существует такое положительное число d , что из условия M (x ,y ) Î V d (x 0 ,y 0 ) следует f (x ,y ) > f (x 0 ,y 0 ) .
Точка M 0 (x 0 ,y 0 ) называется точкой максимума функции z = f (x ,y ) , если существует такое положительное число d , что из условия M (x ,y ) Î V d (x 0 ,y 0 ) следует: f (x ,y ) < f (x 0 ,y 0 ) .
Точки минимума и максимума называются точками экстремума .
§ 1. Основные понятия
Число A называется пределом функции z = f (x ,y ) в точке M 0 (x 0 ,y 0 ):
если для произвольного числа e > 0 найдется такое число d > 0 , что для всех точек M (x ,y ) из d -окрестности точки M 0 (x 0 ,y 0 ) выполняется неравенство
|f (x ,y ) - A |< e .
§ 1. Основные понятия
Функция z = f (x ,y ) называется непрерывной в точке M 0 (x 0 ,y 0 ), если
§ 2. Частные производные
Частной производной по x функции z = f (x ,y ) в точке M 0 (x 0 ,y 0 ) называется предел
если этот предел существует.
§ 2. Частные производные
Совершенно аналогично можно определить частную производную по y функции z = f (x ,y ) в точке M 0 (x 0 ,y 0 ) :
§ 2. Частные производные
Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y . Они называются вторыми частными производными или частными производными второго порядка и обозначаются
zxx ¢¢ , zyy ¢¢ , zxy ¢¢
или
§ 2. Частные производные
Если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности вычислялись частные производные по x и по y .
§ 3. Дифференциал функции двух переменных
Дифференциал представляет собой главную часть приращения функции, линейную относительно приращений её аргументов.
§ 3. Дифференциал функции двух переменных
Дифференцируемая в точке функция обязательно непрерывна в этой точке.
Функция дифференцируема в точке, если обе частные производные этой функции непрерывны в этой точке.
§ 3. Дифференциал функции двух переменных
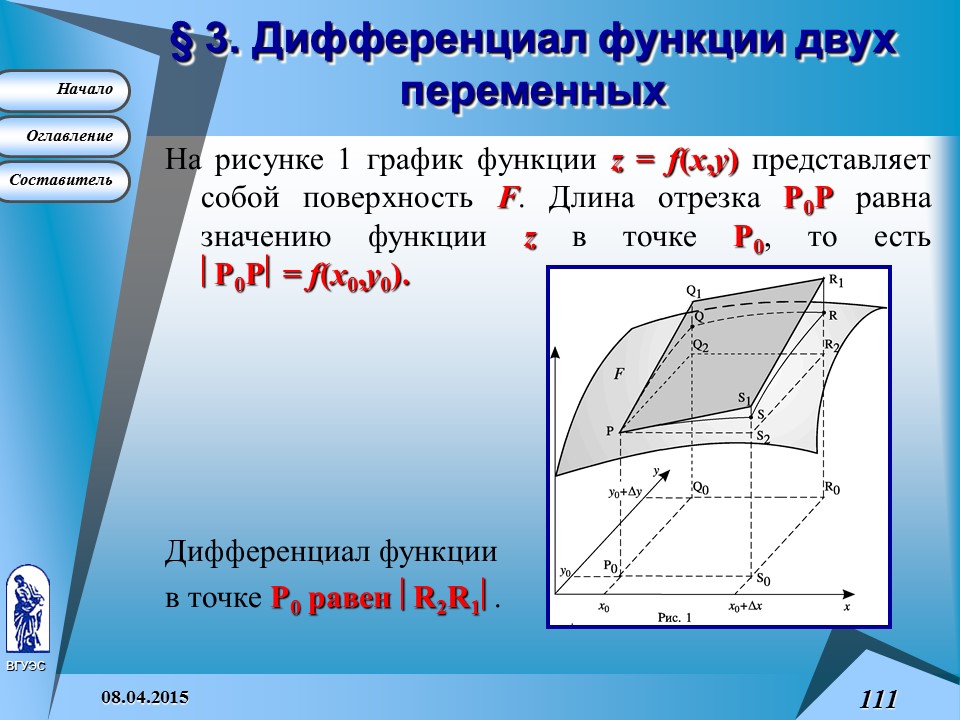
На рисунке 1 график функции z = f (x ,y ) представляет собой поверхность F . Длина отрезка Р0 Р равна значению функции z в точке P0 , то есть ç Р0 Р ç = f (x 0 ,y 0 ).
Дифференциал функции
в точке Р0 равен ç R2 R1 ç .
§ 3. Дифференциал функции двух переменных
Так как df (x 0 ,y 0 ) » D f (x 0 ,y 0 ) , дифференциал df даёт приближенное значение приращения функции при малых значениях приращений аргументов.
§ 4. Производная по направлению
Производной функции z = f (x,y )
в точке M 0 (x 0 ,y 0 )
по направлению l
называется число
§ 4. Производная по направлению
Градиентом или вектором-градиентом функции f (x,y ) в точке (x,y ) Î G называется вектор, который задается формулой
§ 4. Производная по направлению
Производная по направлению от функции z = f (x,y ) в точке M 0 (x 0 ,y 0 ) достигает наибольшего значения, если это направление совпадает с направлением вектора-градиента функции в рассматриваемой точке , так как cos b £ 1 , и равенство достигается только если b = 0 .
Вектор-градиент функции в точке направлен в сторону наискорейшего возрастания функции в этой точке .
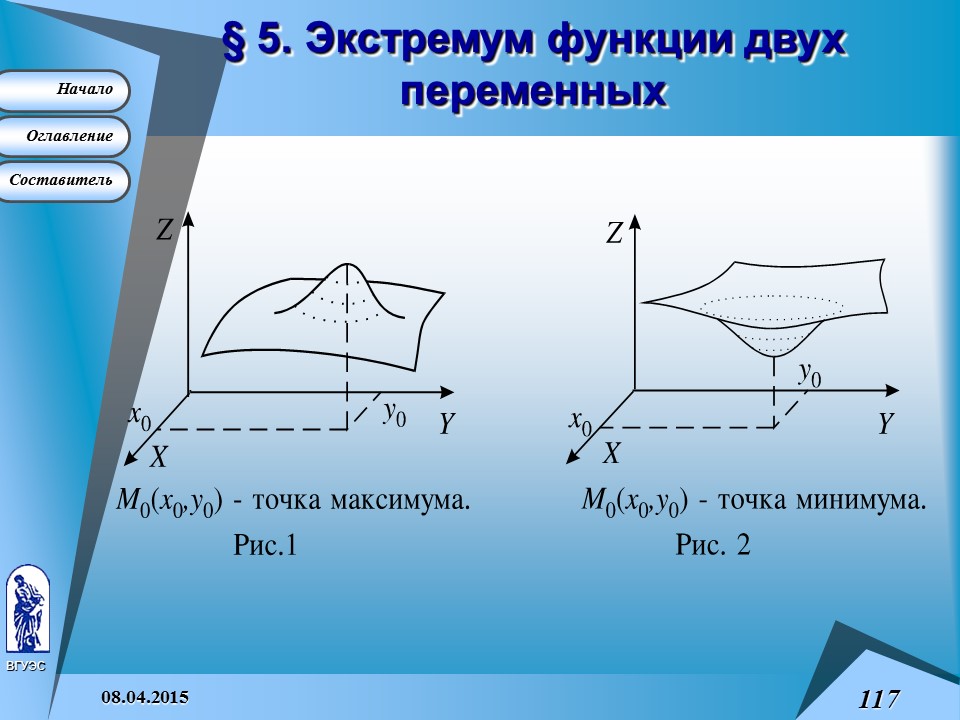
§ 5. Экстремум функции двух переменных
Точка M 0 (x 0 ,y 0 ) является точкой максимума (минимума ) функции z = f (x,y ) , если найдется такая окрестность точки M 0 , что для всех точек M (x,y ) из этой окрестности выполняется неравенство
f (x,y )< f (x 0 ,y 0 ) ( f (x,y )> f (x 0 ,y 0 )).
Точки максимума и минимума называются точками экстремума .
§ 5. Экстремум функции двух переменных
§ 5. Экстремум функции двух переменных
Пусть zx ¢ (x0 ,y0 ) = 0 и zy ¢ (x0 ,y0 ) = 0 , а вторые частные производные функции z непрерывны в некоторой окрестности точки (x0 ,y0 ) . Введем обозначения :
A = zxx ¢¢ (x0 ,y0 );
B = zxy ¢¢ (x0 ,y0 );
C = zyy ¢¢ (x0 ,y0 );
D = AC - B2 .
§ 5. Экстремум функции двух переменных
Тогда, если D < 0 , то в точке (x0 ,y0 ) экстремума нет.
Если D > 0 , то в точке (x0 ,y0 ) экстремум функции z , причем если A > 0 , то минимум, а если A < 0 , то максимум.
Если D = 0 , то экстремум может быть, а может и не быть.
§ 6. Метод наименьших квадратов
Пусть проводится n однородных испытаний или экспериментов, и результатом каждого испытания является пара чисел – значений некоторых переменных x и y .
Испытание с номером i приводит к числам xi , yi .
§ 6. Метод наименьших квадратов
Итогом этих испытаний является таблица:
§ 6. Метод наименьших квадратов
В качестве значений xi часто рассматриваются моменты времени: t 1 , t 2 , ..., t n , взятые через равные промежутки. Тогда таблица
называется временным рядом .
§ 6. Метод наименьших квадратов
Пусть точки с координатами (xi ,yi ) группируются на плоскости вдоль некоторой прямой. Задача заключается в том, чтобы найти параметры a0 и a1 этой прямой :
y = a0 + a1 x , (1)
причем это нужно сделать так, чтобы она лучше любой другой прямой соответствовала расположению на плоскости экспериментальных точек (xi , yi ) .
§ 6. Метод наименьших квадратов
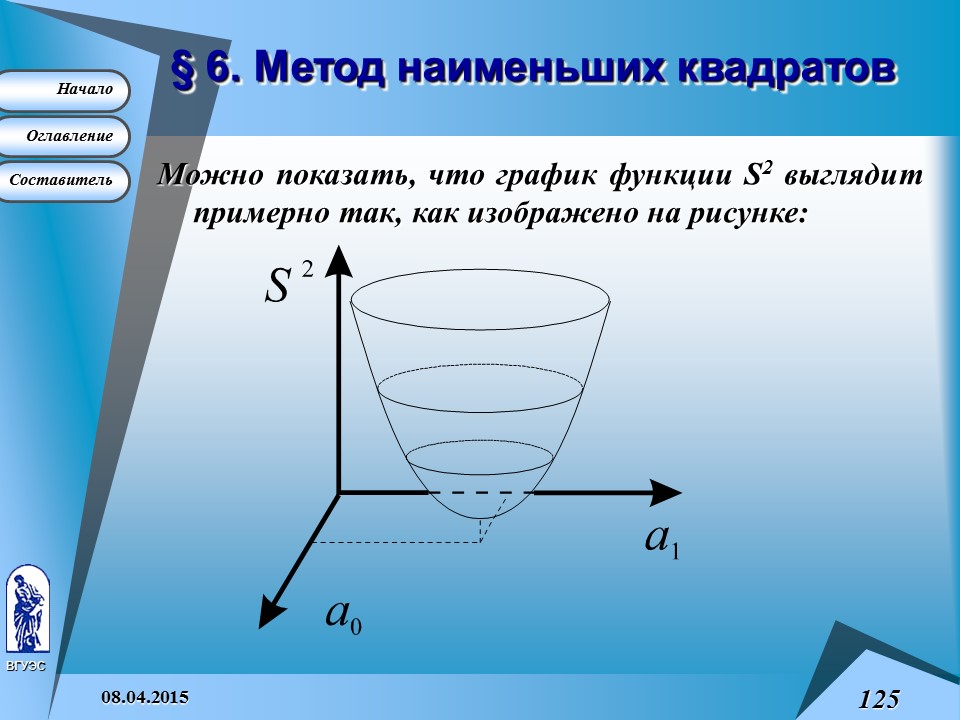
Признаком наилучшей прямой считается минимум суммы квадратов отклонений фактических значений y , полученных из таблицы, от вычисленных по формуле (1). Эта сумма квадратов рассчитывается по формуле
S 2 = (y 1 – (a 0 + a 1 x 1 ))2 + (y 2 – (a 0 + a 1 x 2 ))2 +...+ (y n – (a 0 + a 1 xn ))2 =
§ 6. Метод наименьших квадратов
Можно показать, что график функции S2 выглядит примерно так, как изображено на рисунке:
§ 6. Метод наименьших квадратов
Точку минимума можно искать, используя лишь необходимые условия экстремума:
§ 6. Метод наименьших квадратов
Уравнения (2) и (3) можно преобразовать:
Получилась так называемая система нормальных уравнений относительно неизвестных величин a 0 и a 1 .
§ 6. Метод наименьших квадратов
Формула (1) с параметрами a 0 , a 1 определенными из системы (4) , называется уравнением регрессии .
Прямая линия, описываемая этим уравнением, называется линией регрессии .
Для временных рядов обычно вместо слова “регрессия” употребляется слово тренд .
Комбинаторные формулы
Оглавление
Комбинаторные формулы
Случайный эксперимент, элементарные исходы, события
Вероятностное пространство.
Случай конечного или счетного числа исходов.
Классическое определение вероятности.
Комбинаторные формулы
Пусть имеется множество, состоящее из n элементов.
Перестановками называются множества, составленные из n различных элементов, отличающиеся порядком расположения этих элементов.
Обозначаются перестановки Pn =n!
Комбинаторные формулы
Примеры перестановок:
1) распределение n различных должностей среди n человек;
2) расположение n различных предметов в одном ряду
Комбинаторные формулы
Размещениями из n элементов по k элементов будем называть упорядоченные подмножества, составленные из n элементов по k в каждом.
Число размещений из n элементов по k элементов обозначается
(читается "А из n по k ").
Комбинаторные формулы
Сочетаниями из n элементов по k элементов называются подмножества, составленные из n элементов по k в каждом, отличающиеся хотя бы одним элементом.
Комбинаторные формулы
Формула для подсчёта числа сочетаний
Случайный эксперимент, элементарные исходы, события
Случайным (стохастическим ) экспериментом или испытанием называется осуществление какого-либо комплекса условий, который можно практически или мысленно воспроизвести сколь угодно большое число раз
Случайный эксперимент, элементарные исходы, события
Примеры случайного эксперимента :
подбрасывание монеты, извлечение одной карты из перетасованной колоды, подсчет числа автомобилей в очереди на бензоколонке в данный момент.
Случайный эксперимент, элементарные исходы, события
Явления, происходящие при реализации этого комплекса условий, то есть в результате случайного эксперимента, называются элементарными исходами .
Случайный эксперимент, элементарные исходы, события
Событием ( случайным событием )
называется результат опыта, который при выполнении определенного комплекса условий может произойти или не произойти.
Случайный эксперимент, элементарные исходы, события
Говорят, что те исходы, из которых состоит событие А , благоприятствуют событию А .
События удобно изображать в виде рисунка, который называется диаграммой Венна .
Случайный эксперимент, элементарные исходы, события
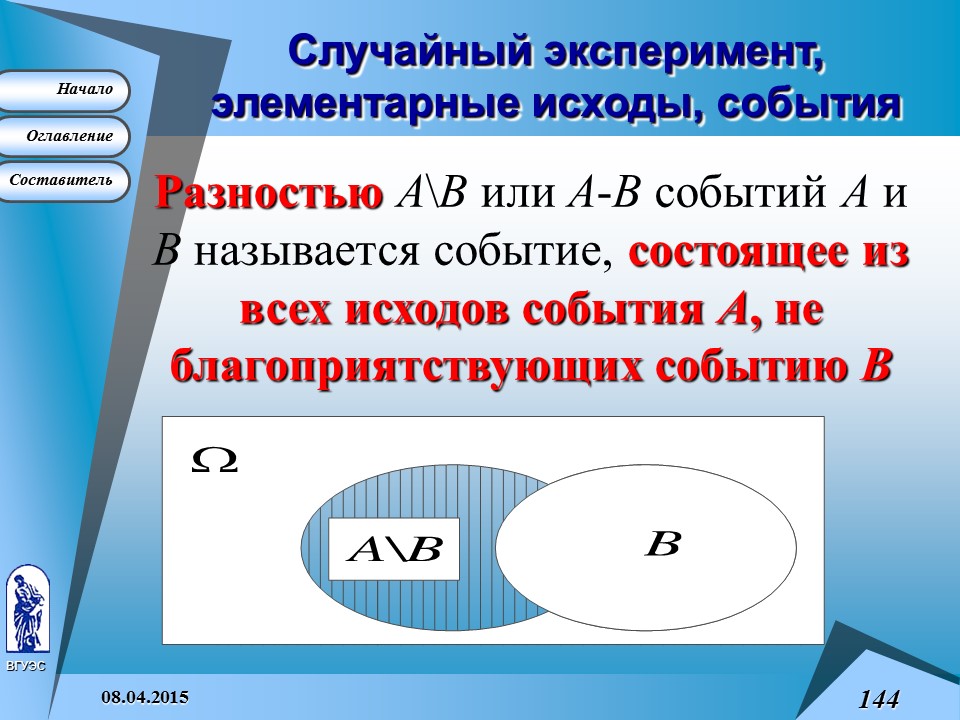
На рисунке 1 пространство элементарных исходов W изображено в виде прямоугольника, а множество элементарных исходов, благоприятствующих событию A , заключено в эллипс.
Случайный эксперимент, элементарные исходы, события
Суммой (объединением) двух событий А и B (обозначается A UB ) называется событие, состоящее из всех элементарных исходов, принадлежащих по крайней мере одному из событий А или B .
Случайный эксперимент, элементарные исходы, события
Произведением (пересечением)
A B событий А и B называется событие, состоящее из всех тех элементарных исходов, которые принадлежат и А и B .
Случайный эксперимент, элементарные исходы, события
Разностью А \B или А -B событий А и B называется событие, состоящее из всех исходов события А , не благоприятствующих событию B
Случайный эксперимент, элементарные исходы, события
События А и B называются несовместными , если нет исходов, принадлежащих и А и B , то есть A B = Æ.
Вероятностное пространство.
Случай конечного или счетного числа исходов.
Каждому элементарному исходу w i пространства W соответствует некоторая неотрицательная числовая характеристика Pi шансов его появления, называемая вероятностью исхода w i , причем
Вероятностное пространство.
Случай конечного или счетного числа исходов.
Вероятность любого события А определяется как сумма вероятностей всех элементарных исходов, благоприятствующих событию А . Обозначим ее Р (А ).
Классическое определение вероятности.
Возможна ситуация, когда пространство элементарных исходов состоит из конечного числа N элементарных исходов, причем случайный эксперимент таков, что вероятности осуществления каждого из этих N элементарных исходов представляются равными.
Классическое определение вероятности.
В данном классе ситуаций вероятность события определяется как отношение числа благоприятных исходов к общему числу всех возможных исходов
Статистическое определение вероятности.
Оглавление
Статистическое определение вероятности
Геометрическая вероятность
Непрерывное вероятностное пространство
Условия вероятности
Статистическое определение вероятности.
Вероятность P( w i ) определяется как предел относительной частоты появления исхода w i в процессе неограниченного увеличения числа случайных экспериментов n , то есть
где mn ( w i ) – число случайных экспериментов (из общего числа n произведенных случайных экспериментов), в которых зарегистрировано появление элементарного исхода w i .
Геометрическая вероятность.
Если между множеством W элементарных исходов случайного эксперимента и множеством точек некоторой плоской фигуры S (сигма большая) можно установить взаимно-однозначное соответствие, а также можно установить взаимно-однозначное соответствие между множеством элементарных исходов, благоприятствующих событию А , и множеством точек плоской фигуры s (сигма малая), являющейся частью фигуры S , то
где s — площадь фигуры s , S — площадь фигуры S .
Непрерывное вероятностное пространство
Непрерывное вероятностное пространство
Условные вероятности
Условные вероятности
Формула полной вероятности.
Оглавление
Формула полной вероятности
Формула Байеса
Повторные независимые испытания. Формула Бернулли.
Случайная величина, распределенная по закону Бернулли.
Формула полной вероятности.
Пусть имеется группа событий
H 1 , H 2 ,..., Hn ,
образующих полную группу несовместных событий,
называемых
гипотезами .
Формула полной вероятности.
Пусть А - некоторое событие, которое может произойти только с одной из этих гипотез. Тогда имеет место формула полной вероятности :
P (A ) = P (A / H 1 )P (H 1 ) + P (A / H 2 )P (H 2 ) + ...+ P (A / Hn )P (Hn ) =
Формула Байеса.
Повторные независимые испытания. Формула Бернулли.
формула Бернулли :
По формуле Бернулли рассчитывается вероятность появления события A "x "раз в n повторных независимых испытаниях, где p - вероятность появления события A в одном испытании, q - вероятность непоявления события в одном испытании.
Повторные независимые испытания. Формула Бернулли.
Сформулированные условия проведения испытаний иногда называются "схемой повторных независимых испытаний " или "схемой Бернулли "
Число x появления события A в n повторных независимых испытаниях называется частотой .
Случайная величина, распределенная по закону Бернулли.
При двух заданных числах:
1) n - количестве повторных независимых испытаний,
2) p - вероятности события A в одном испытании
можно по формуле Бернулли подсчитать значение вероятности каждого целого числа x , где x – число появлений события A в n испытаниях (частота появления события A ) .
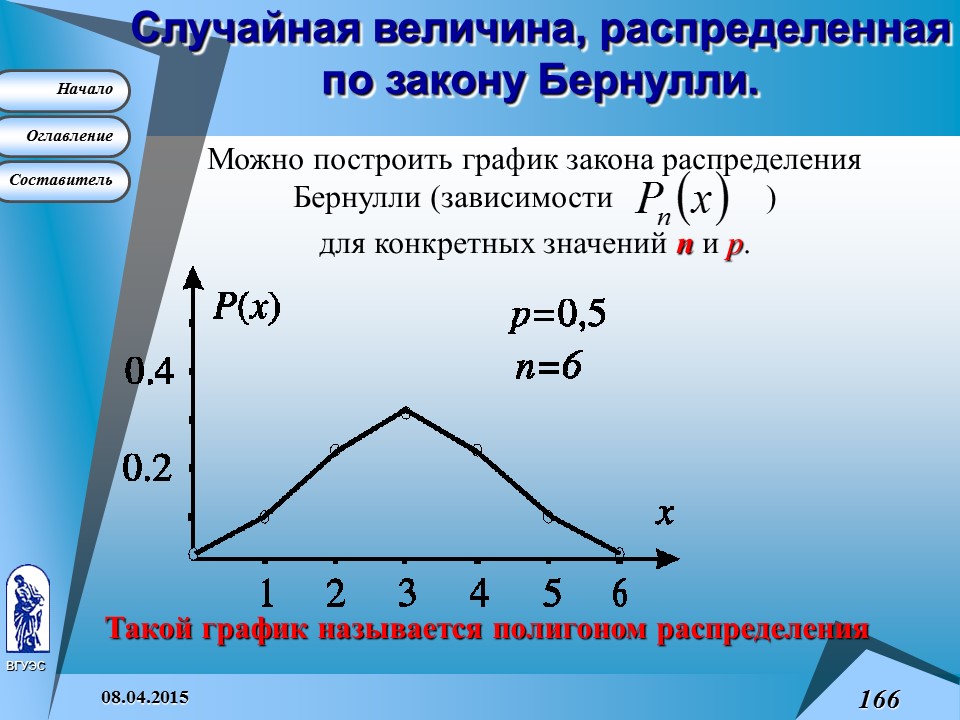
Случайная величина, распределенная по закону Бернулли.
Можно построить график закона распределения Бернулли (зависимости )
для конкретных значений n и p .
Асимптотические формулы для формулы Бернулли.
Асимптотические формулы для формулы Бернулли.
Такие формулы, которые получаются при условии
называются асимптотическими .
Асимптотические формулы для формулы Бернулли.
Если n достаточно велико, а p - величина очень малая, для формулы Бернулли имеет место приближенная (асимптотическая) формула
Здесь l =np ( l - греческая буква "лямбда "). Эта формула называется формулой Пуассона .
Асимптотические формулы для формулы Бернулли.
Если n достаточно велико, p не сильно отличается от 0,5 , имеет место формула Муавра-Лапласа , иногда называемая локальной формулой Лапласа.
где
Дискретные случайные величины.
Оглавление
- Дискретные случайные величины.
- Математическое ожидание случайной величины.
- Дисперсия случайной величины.
- Свойства дисперсии.
Дискретные случайные величины.
Каждому исходу случайного эксперимента поставим в соответствие единственное число xk — значение случайной величины. Тогда естественно рассматривать случайную величину как функцию, заданную на множестве исходов случайного эксперимента .
Случайной называется величина, которая может принимать лишь одно из своих возможных значений, заранее неизвестно какое.
Дискретные случайные величины.
Случайная величина, значения которой изолированы друг от друга (каждому значению можно придать порядковый номер) называется
дискретной .
Будем обозначать дискретные случайные величины
X , Y , Z , …,
а значения этих величин
xi , yj , zk , ...
Дискретные случайные величины.
Если говорится, что задана случайная величина X , это значит, что каждому исходу w i случайного эксперимента поставлено в соответствие единственное число x i , что записывается в виде равенства
x i = X ( w i ) .
Дискретные случайные величины.
Если каждому значению xi
случайной величины X поставлена в соответствие вероятность pi , с которой случайная величина принимает это значение, такое соответствие называется законом распределения дискретной случайной величины X
Математическое ожидание случайной величины.
Математическое ожидание
М x (или М ( X ))
случайной величины X определяется формулой:
Математическое ожидание случайной величины.
Свойства математического ожидания:
- Если k – константа , то M(k)=k
- M(kX)=kM(X)
- Если X1 , X2 …,Xn попарно независимые случайные величины, то
-
Дисперсия случайной величины.
Дисперсия D(X) случайной величины X определяется формулой
D (X) = M ( X – M (X) )2
Дисперсия случайной величины — это математическое ожидание квадрата отклонения случайной величины от её математического ожидания .
Свойства дисперсии.
- Если k – число , то D (k )=0
- Если k – число , то D ( k X ) = k 2 D (X) .
- Для попарно независимых случайных величин X 1 , X 2 , ¼ , Xn справедливо равенство
- D (X-Y)= D (X)+ D (Y)
Биномиальный закон распределения.
Биномиальный закон распределения.
Пусть заданы числа
n Î N и p (0 £ p £ 1) .
Тогда каждому целому числу из промежутка [0; n ] можно поставить в соответствие вероятность, рассчитанную по формуле Бернулли . Получим закон распределения случайной величины (назовём её X )
Биномиальный закон распределения.
Биномиальный закон распределения.
Для случайной величины X , имеющей закон распределения Бернулли , математическое ожидание и дисперсия определяются формулами:
Непрерывные случайные величины.
Непрерывные случайные величины.
Случайная величина, значения которой сплошь заполняют некоторый промежуток, называется непрерывной .
Непрерывные случайные величины.
Пусть X – непрерывная случайная величина. Функция F (x ) , которая определяется равенством
,
называется интегральной функцией распределения или просто функцией распределения
случайной величины X .
Непрерывные случайные величины.
Непосредственно из определения следует равенство
Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению
Плотность распределения ¦ (х ) называют дифференциальной функцией распределения .
Непрерывные случайные величины.
Функция распределения F (x ) случайной величины X имеет следующие свойства:
1. F (x ) — непрерывная возрастающая функция.
2.
3. Приращение F (x ) на промежутке (х 1 ; х 2 ) равно вероятности того, что случайная величина X принимает значение из этого промежутка:
F (x 2 ) – F (x 1 ) = P (x 1 < X £ x 2 )
Непрерывные случайные величины.
Заметим, что для непрерывной случайной величины X справедливы равенства:
P (x 1 < X £ x 2 ) = P (x 1 < X < x 2 ) = P (x 1 £ X < x 2 ) = P (x 1 £ X £ x 2 )
Непрерывные случайные величины.
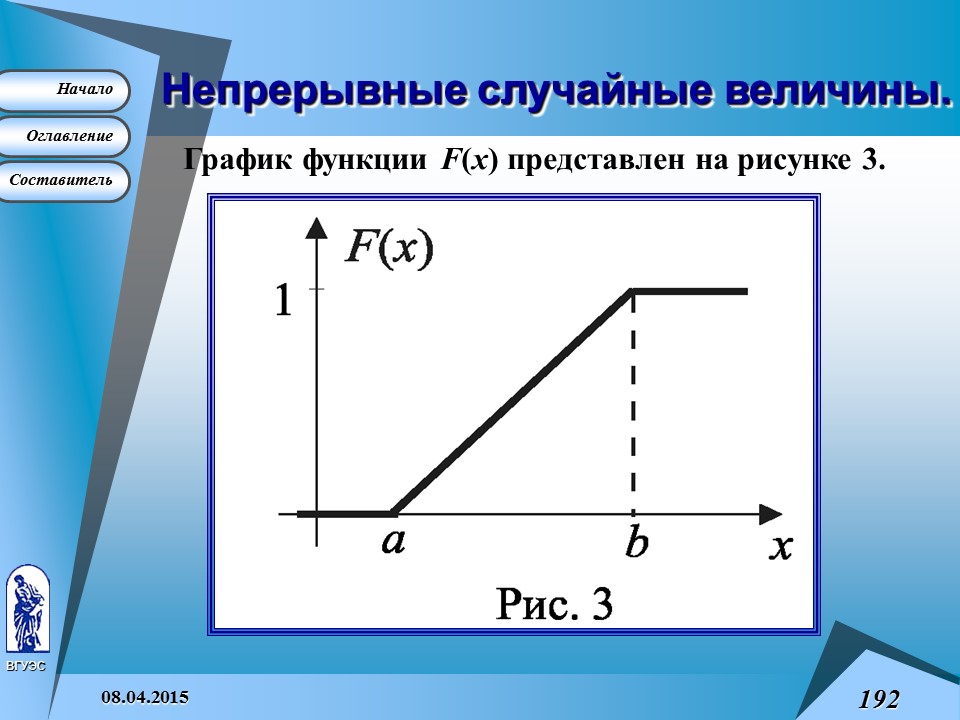
Для равномерного распределения функция F (x ) имеет вид :
Непрерывные случайные величины.
График функции F (x ) представлен на рисунке 3.
Непрерывные случайные величины.
Для равномерно распределенной случайной величины X справедливы следующие равенства:
1.
2.
3.
Правило 3-х s (трех “сигм”).
Правило 3-х s (трех “сигм”) .
Нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3 s .
Распределение c 2.
Оглавление
- Распределение c 2
- Распределение Стьюдента
- Распределение Фишера
Распределение c 2 .
Пусть имеется n независимых случайных величин X1 , X2 , ..., Xn , распределенных по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице.
Тогда случайная величина распределена по закону, который называется
“распределение c 2 ” или
“распределение Пирсона ”.
Число n называется числом степеней свободы .
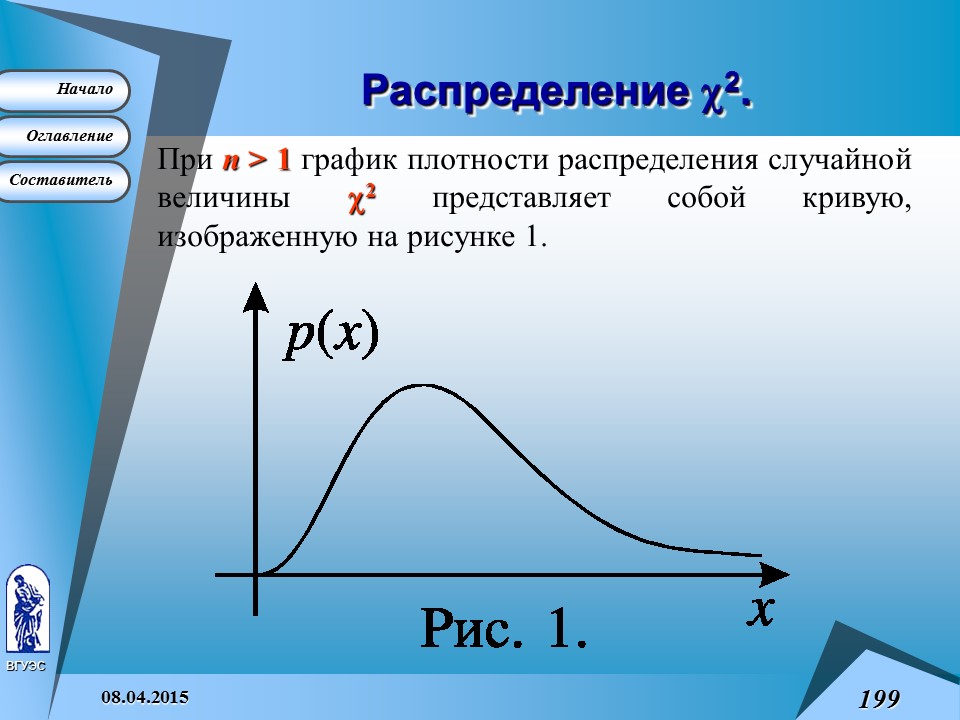
Распределение c 2 .
При n > 1 график плотности распределения случайной величины c 2 представляет собой кривую, изображенную на рисунке 1.
Распределение Стьюдента.
Закон распределения случайной величины t называется законом распределения Стьюдента с k степенями свободы.
где X и Y – независимые случайные величины, причем X – нормально распределенная случайная величина с параметрами M (X) = 0 и D (X) = 1 , а Y распределена по закону c 2 c k степенями свободы.
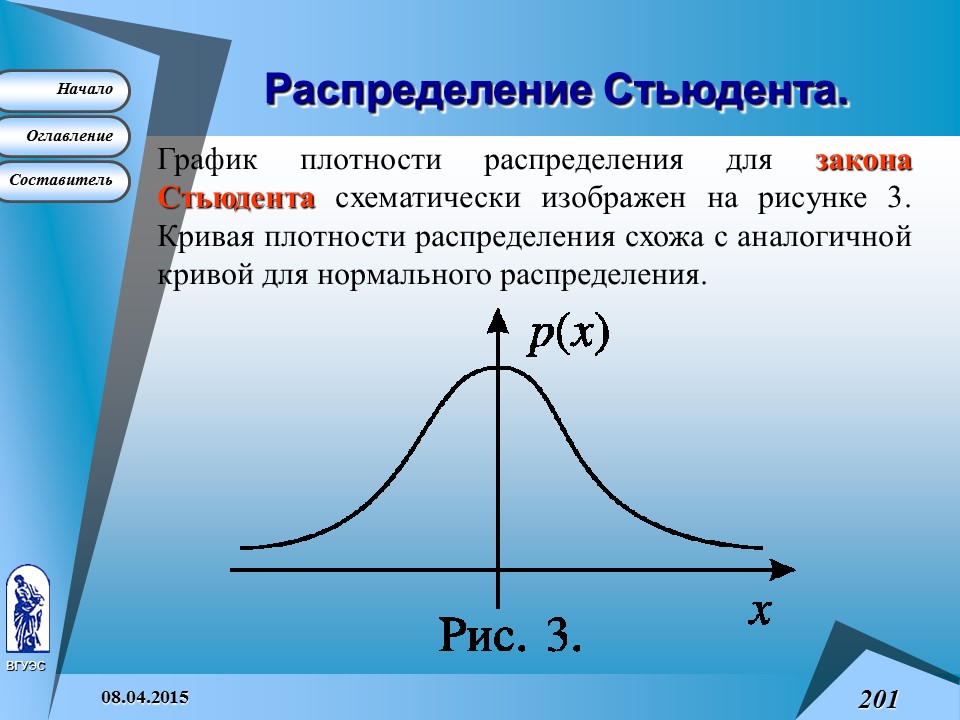
Распределение Стьюдента.
График плотности распределения для закона Стьюдента схематически изображен на рисунке 3. Кривая плотности распределения схожа с аналогичной кривой для нормального распределения.
Распределение Фишера.
Случайная величина F распределена по закону, называемому законом распределения Фишера с k 1 и k 2 степенями свободы.
где X – случайная величина, распределенная по закону c 2 с k 1 степенями свободы, а Y – случайная величина, распределенная по закону c 2 с k 2 степенями свободы.
Математическая статистика.
Оглавление
- Математическая статистика.
- Выборочный метод.
- Вариационный ряд.
- Точечные оценки параметров генеральной совокупности.
Математическая статистика.
Основной задачей математической статистики является разработка методов получения научно обоснованных выводов о массовых явлениях и процессах из данных наблюдений и экспериментов.
Выборочный метод.
Пусть нам нужно обследовать количественный признак в партии экземпляров некоторого товара. Проверку партии можно проводить двумя способами:
1) провести сплошной контроль всей партии;
2) провести контроль только части партии.
Выборочный метод.
При втором способе множество случайным образом отобранных объектов называется выборочной совокупностью или выборкой .
Все множество объектов, из которого производится выборка, называется генеральной совокупностью .
Число объектов в выборке называется объемом выборки .
Выборочный метод.
Выборки разделяются на повторные (с возвращением) и бесповторные (без возвращения).
Выборка должна достаточно полно отражать особенности всех объектов генеральной совокупности, иначе говоря, выборка должна быть репрезентативной (представительной ).
Выборочный метод.
Выборки различаются по
способу отбора .
1. Простой случайный отбор.
2. Типический отбор.
3. Механический отбор.
4. Серийный отбор.
Выборочный метод.
В дальнейшем под генеральной совокупностью мы будем подразумевать не само множество объектов, а множество значений случайной величины, принимающей числовое значение на каждом из объектов .
Выборочный метод.
Таким образом на выборку будем смотреть как на совокупность независимых случайных величин
X 1 , X 2 , ..., X n , распределенных так же, как и случайная величина X , представляющая генеральную совокупность .
Выборочные значения x 1 , x 2 , ..., xn – это значения, которые приняли эти случайные величины в результате 1-го , 2-го , ..., n -го эксперимента .
Вариационный ряд.
Из выборки объема n получаем значения этой случайной величины в виде ряда из n чисел:
x 1 , x 2 ,..., xn .
Эти числа называются значениями признака. Среди чисел ряда могут быть одинаковые числа. Если значения признака упорядочить, то есть расположить в порядке возрастания или убывания, написав каждое значение лишь один раз, а затем под каждым значением xi признака написать число mi , показывающее сколько раз данное значение встречается в ряду:
Вариационный ряд.
Вариационный ряд.
Если промежуток между наименьшим и наибольшим значениями признака в выборке разбить на несколько интервалов одинаковой длины, каждому интервалу поставить в соответствие число выборочных значений признака, попавших в этот интервал, то получим интервальный вариационный ряд .
Точечные оценки параметров генеральной совокупности.
Пусть выборка объема n представлена в виде вариационного ряда.
Назовем выборочной средней величину
Величина
называется относительной частотой значения признака xi .
Точечные оценки параметров генеральной совокупности.
Выборочная оценка параметра, представляющая собой число, называется точечной оценкой .
Выборочную дисперсию
можно считать точечной оценкой дисперсии D (X) генеральной совокупности.
Точечные оценки параметров генеральной совокупности.
Пусть выборочный параметр Q* рассматривается как выборочная оценка параметра Q генеральной совокупности и при этом выполняется равенство
M ( Q*) = Q .
Такая выборочная оценка называется несмещенной .
Точечные оценки параметров генеральной совокупности.
Выборочная дисперсия не является несмещенной оценкой дисперсии генеральной совокупности.
Та оценка, которая имеет наименьшую дисперсию называется эффективной .
Полученная из выборки объема n точечная оценка Q* n параметра Q генеральной совокупности называется состоятельной , если она сходится по вероятности к Q .
Интервальные оценки.
Оглавление
- Интервальные оценки.
- Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
- Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии.
- Доверительный интервал для дисперсии нормального распределения.
Интервальные оценки.
Введем понятие интервальной оценки неизвестного параметра генеральной совокупности (или случайной величины X , определенной на множестве объектов этой генеральной совокупности).
Обозначим этот параметр через Q .
Интервальные оценки.
По сделанной выборке по определенным правилам найдем числа Q 1 и Q 2 , так чтобы выполнялось условие:
P ( Q 1 < Q < Q 2 ) =P ( Q Î ( Q 1 ; Q 2 )) = g
Числа Q 1 и Q 2 называются доверительными границами , интервал ( Q 1 , Q 2 ) — доверительным интервалом
для параметра Q .
Число g называется доверительной вероятностью или надежностью сделанной оценки.
Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
Для любого g
Î
[0;1]
можно по таблице найти такое число t
, что
F
( t )=
g
/ 2
.
Это число t иногда называют квантилем .
Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
Смысл формулы
состоит в следующем:
с надежностью g доверительный интервал
покрывает неизвестный параметр a = M (X) генеральной совокупности. Можно сказать иначе: точечная оценка x определяет значение параметра M (X)
с точностью и надежностью g .
Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии.
Задача заключается в том, чтобы по заданной надежности g и по числу степеней свободы n – 1 найти такое число t g , чтобы выполнялось равенств о
или эквивалентное равенство
Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии.
Чтобы определить значение t g по величине g , равенство (2) преобразуем к виду:
Теперь по таблице для случайной величины t , распределенной по закону Стьюдента , по вероятности 1 – g и числу степеней свободы n – 1 находим t g . Формула (3) дает ответ поставленной задачи.
Доверительный интервал для дисперсии нормального распределения.
Формула , по которой находится доверительный интервал для стандартного отклонения:
Задачи статистической проверки гипотез.
Задачи статистической проверки гипотез.
Гипотезы о значениях параметров распределения или о сравнительной величине параметров двух распределений называются параметрическими гипотезами .
Гипотезы о виде распределения называются непараметрическими гипотезами .
Задачи статистической проверки гипотез.
Проверить статистическую гипотезу – это значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой.
Статистический критерий – это случайная величина, закон распределения которой (вместе со значениями параметров) известен в случае, если принятая гипотеза справедлива.
Этот критерий называют еще критерием согласия (имеется в виду согласие принятой гипотезы с результатами, полученными из выборки).
Задачи статистической проверки гипотез.
Гипотезу, выдвинутую для проверки ее согласия с выборочными данными, называют нулевой гипотезой и обозначают H 0 .
Вместе с гипотезой H 0 выдвигается альтернативная или конкурирующая гипотеза, которая обозначается H 1 .
Задачи статистической проверки гипотез.
Если K в – значение критерия K , рассчитанное по выборочным данным, превзошло значение K кр , это означает, что выборочные данные не дают основания для принятия нулевой гипотезы H 0
В этом случае говорят, что
гипотеза H 0 не согласуется с выборочными данными и должна быть отвергнута .
Задачи статистической проверки гипотез.
Если K в не превосходит K кр ,
то говорят, что
выборочные данные
не противоречат гипотезе H 0 ,
и нет оснований отвергать эту гипотезу.
Задачи статистической проверки гипотез.
Область K>K кр называется критической областью.
Если значение K в попадает в критическую область, то гипотеза H 0 отвергается .
Область K<K кр называется областью принятия гипотезы .
Если значение K в попадает в
область принятия гипотезы, то гипотеза H 0 принимается .
Задачи статистической проверки гипотез.
Отвержение правильной гипотезы называется ошибкой первого рода .
Вероятность a называется уровнем значимости. Таким образом
уровень значимости – это вероятность совершения ошибки первого рода .
Задачи статистической проверки гипотез.
Чем меньше уровень значимости, тем меньше вероятность отвергнуть проверяемую гипотезу H 0 , когда она верна, то есть совершить ошибку первого рода.
Но с уменьшением уровня значимости расширяется область принятия гипотезы H 0 и увеличивается вероятность принятия проверяемой гипотезы, когда она неверна, то есть когда предпочтение должно быть отдано конкурирующей гипотезе .
Задачи статистической проверки гипотез.
Принятие неверной гипотезы называется ошибкой второго рода .
Число b – это вероятность ошибки второго рода.
Число 1 – b , равное вероятности того, что не совершается ошибка второго рода, называется
мощностью критерия .
Составитель
доцент кафедры математики и моделирования ВГУЭС
Шуман Галина Ивановна