| Скачать .docx |
Реферат: Лабораторная работа: Исследование характеристик одиночных и связанных колебательных кон
Министерство образования Российской Федерации
Новгородский государственный университет имени Ярослава Мудрого
Кафедра '' Радиосистем ''
Исследование характеристик одиночных колебательных контуров.
Лабораторная работа по дисциплине
'' Радиотехнические цепи и сигналы''
Цель работы: изучение частотных характеристик (АЧХ и ФЧХ) и параметров последовательного и параллельного колебательных контуров.
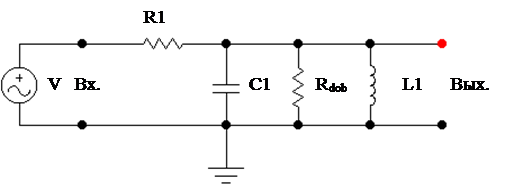 Схемы установки:
Схемы установки:
Рисунок 1- Параллельный колебательный контур
Параметры параллельного контура:
R1=1 кОм;
С1=10 nF;
f0=50 кГц.
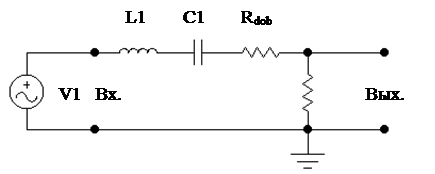 |
Рисунок 2- Последовательный колебательный контур
Параметры последовательного колебательного контура:
R1=10 Ом;
C1=10 nF;
fo=50 кГц
Расчетные формулы:
![]() =0,101 Гн
=0,101 Гн
где
f = 50 кГц
С=10 нФ;
Выполнение работы:
1) Сняли АЧХ и ФЧХ обоих контуров при четырёх значениях Rdob:
a) Rdob=1 кOм;
b) Rdob=100 Ом;
c) Rdob=10 Ом;
d) Rdob= ¥ (для параллельного контура);
e) Rdob=0 (для последовательного контура).
Смотри рисунки 3-10.
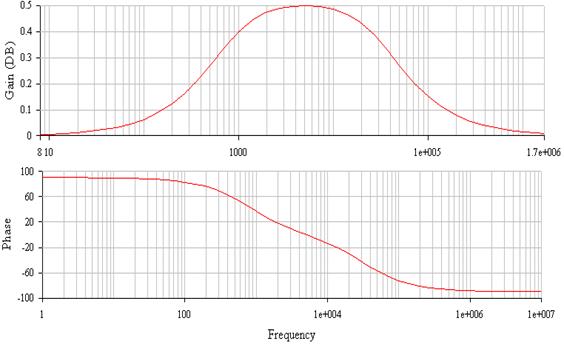
Рисунок 3 АЧХ, ФЧХ последовательного колебательного контура при Rдоп=1кОм
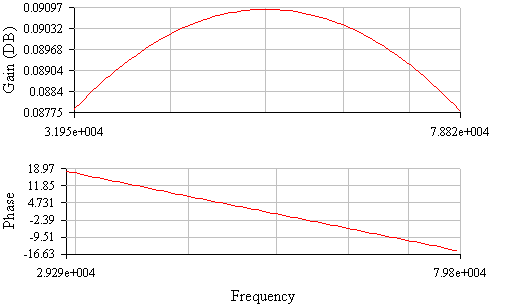
Рисунок 4 АЧХ,ФЧХ последовательного колебательного контура при Rдоп=100 Ом
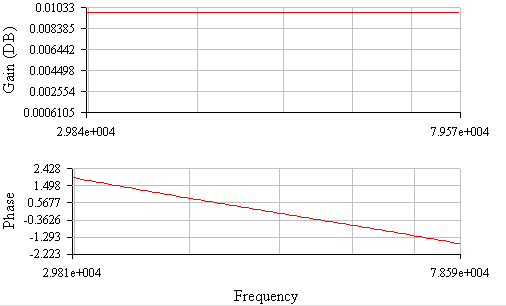
Рисунок 5 АЧХ,ФЧХ последовательного колебательного контура при Rдоп=10 Ом
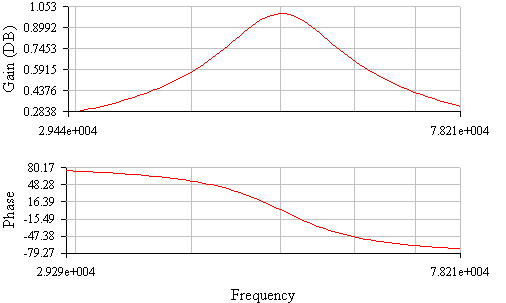
Рисунок 6 АЧХ,ФЧХ последовательного колебательного контура при Rдоп= ¥
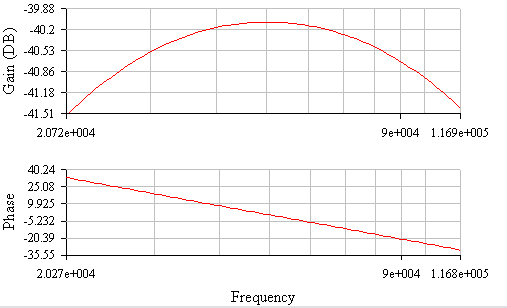
Рисунок 7 АЧХ,ФЧХ параллельного колебательного контура при Rдоп= 1кОм
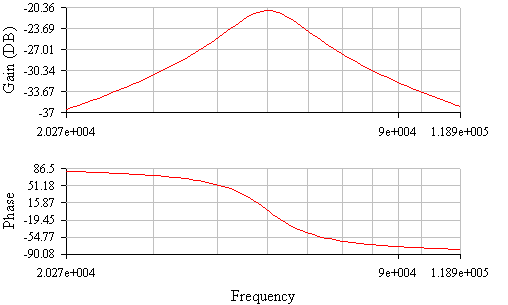
Рисунок 8 АЧХ,ФЧХ параллельного колебательного контура при Rдоп= 100 Ом
Рисунок 9 АЧХ,ФЧХ параллельного колебательного контура при Rдоп= 10 Ом
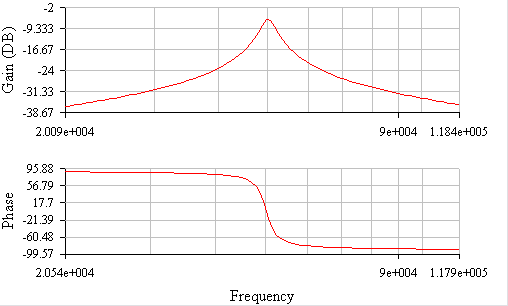
Рисунок 10 АЧХ,ФЧХ параллельного колебательного контура при Rдоп= 0 Ом
2) Рассчитали по полученным данным параметры контуров: ∆f0,707, Q, ρ, Rэо, τк. Результаты смиотри в таблице 1
Таблица1 Результаты измерений и расчетов
| R доб,Ом | ∆f0,707б,кГц | Q | ρ,Ом | Rэо,Ом | τk,mkC | ||||||
| Пар | посл | пар | посл | пар | посл | пар | пар | ||||
| 1000 | 31,9 | 1050 | 0,784 | 0,024 | 1252 | 0,238 | 1567 | 31,348 | 0,952 | ||
| 100 | 175 | 43 | 0,143 | 0,581 | 535 | 5,814 | 286 | 5,714 | 23,256 | ||
| 10 | 1610 | 8 | 0,016 | 3,125 | 176 | 31,25 | 31 | 0,621 | 125 | ||
| 0 | ------ | 5,5 | -------- | 4,545 | ------- | 45,46 | -------- | ------ | 181,82 | ||
| ¥ | 16 | ----- | 1,563 | ------- | 1768 | ------- | 3125 | 62,50 | ------- | ||
Вывод: Таким образом, мы изучили и сняли частотные характеристики (АЧХ и ФЧХ) и параметры последовательного и параллельного колебательных контуров. Из полученных данных следует, что ширина полосы пропускания последовательного колебательного контура растет с увеличением добавочного сопротивления, а ширина полосы пропускания параллельного колебательного контура уменьшается с увеличением добавочного сопротивления. Можно заметить, что добротность последовательного колебательного контура стремиться к максимальному значению при уменьшении нагрузочного сопротивления, а для параллельного колебательного контура наблюдается обратная зависимость.
Исследование характеристик системы двух связанных колебательных контуров.
Лабораторная работа по дисциплине
''РТЦиС''
Цель работы : изучение частотных характеристик (АЧХ и ФЧХ) в системе двух связанных колебательных контуров.
Схемы установки:
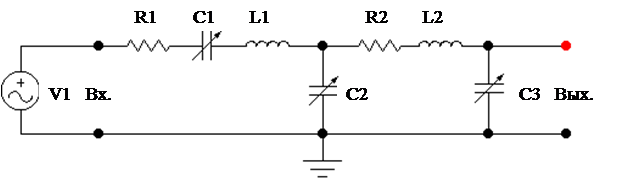 |
Рис.1. Система двух связанных колебательных контуров
Параметры контура:
R1=100 Ом;
R2=10 Ом:
C1= С3=10 nF;
С2=400 nF: - элемент связи между контурами
fo=50 кГц.
Расчетные формулы:
![]() =1.01 мГн
=1.01 мГн
где
f = 50 кГц
С=10 нФ;
Выполнение работы:
1. Собрали схему изображенную на рисунке 1.
2. Отградуировали шкалу изменения величины связи С2 в значениях фактора связи А.
3. Построили градуировочную таблицу зависимости А=f(C2).
Таблица 1 - Зависимость фактора связи А от емкости связи С2.
| A | 0,3 | 0,5 | 0,75 | 1 | 2 | 3 |
| UC3 норм | 0,55 | 0,8 | 0,96 | 1 | 0,8 | 0,6 |
| С2, нФ | 344 | 204 | 118 | 100 | 46 | 12 |
Где:
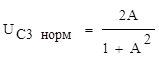
Найденное значение С2 при А=1 занесли в таблицу, при этом максимальное значение АЧХ приняли равным за 1. Построили градуировочный график А=f (C2) (Рис.2).
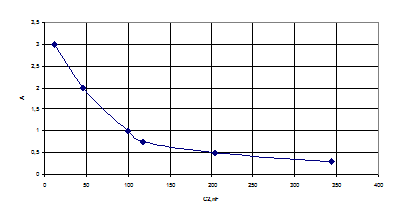
Рисунок 2 - Градуировочный график зависимости А от С2
4. Исследовали АЧХ, ФЧХ и полосу пропускания системы связанных контуров в зависимости от фактора связи А (А=0,3; 1; 2).
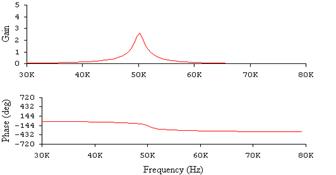 |
Рисунок.3 - АЧХ и ФЧХ при А=0,3.
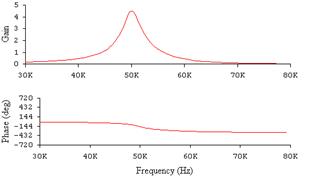
Рисунок 4 - АЧХ и ФЧХ при А=1
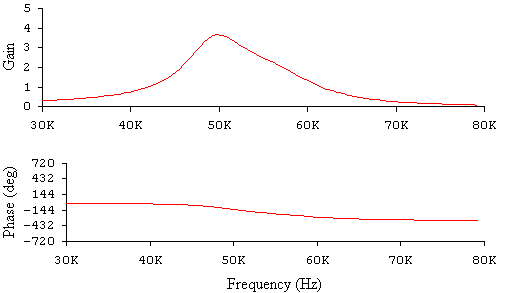
Рисунок 5 - АЧХ и ФЧХ при А=2
По графикам определили полосу пропускания и h(A) - отношение полосы пропускания системы к полосе пропускания одиночного контура, результаты занесли в таблицу 2.
Таблица 2 - Результаты измерений и расчетов
| А | UC3 max, dB | f0, кГц | 0,707UC3 max , dB | fн, кГц | fв, кГц | П, кГц | h(A) |
| 2 | 3.66 | 50 | 2.601 | 47 | 55 | 8 | 2.51 |
| 1 | 4.57 | 50 | 3.23 | 48.5 | 51.7 | 3.2 | 1.5 |
| 0.3 | 2.51 | 50 | 1.78 | 48.8 | 50 | 1.2 | 0.7 |
Рассчитали и построили график зависимости h(A) - отношение полосы пропускания системы к полосе пропускания одиночного контура.(Рисунок 6), где
![]()
![]()
Нанесли на графике точки, полученные экспериментально(таблица 2).
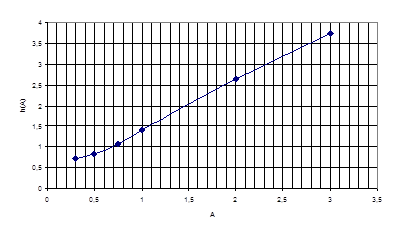
Рисунок 6 - Зависимость h(A).
Вывод: При факторе связи А меньшем 1 АЧХ имеет одногорбый характер, а при А большем 1 наблюдается появление двугорбости АЧХ. Таким образом, системой связанных контуров можно обеспечить полосу пропускания более широкую чем одиночным контуром. При А=2,41 полоса пропускания становится предельной, т.е. провал двугорбой частотной характеристики становится меньше уровня 0.707.