| Скачать .docx |
Курсовая работа: Синтез химико-технологической схемы
Кафедра математического моделирования и оптимизации химико-технологических процессов
КУРСОВАЯ РАБОТА
Тема: «Синтез химико-технологической схемы»
Учебная дисциплина Структурный анализ химических технологий
Студент _____________________________
Факультет 1
Курс 4
Группа 131
Руководитель _________________
Оценка за курсовую работу ____________
Санкт-Петербург
2007
Содержание
Задание
Введение
1. Практическая часть
1.1 Обработка экспериментальных данных
1.1.1 Нахождение параметров уравнения Аррениуса методом МНК
1.1.2 Получение статистической модели абсорбера с помощью метода Брандона
1.2 Математическое описание аппаратов
1.2.1 Реакторы идеального вытеснения
1.2.2 Абсорберы
1.3 Синтез оптимальной тепловой системы с помощью эвристического метода
Выводы
Список используемой литературы
Задание
Требуется синтезировать ХТС, работающую по следующей технологии:
Смесь, состоящую из компонентов А и B и инертного компонента нагревается в системе теплообмена до t1, поступает в реактор, где протекает обратимая реакция: A+0,5B=C+q, где q=21200 кал/моль – тепловой эффект реакции.
Реакция характеризуется константой скорости k=f(t) и константой равновесия К=f(t), для которых имеются экспериментальные данные.
Поскольку реакция равновесная и экзотермическая, то для повышения равновесной степени превращения реакционная смесь должна проходить несколько реакторов с промежуточным охлаждением между ними.
После прохождения m реакторов смесь поступает в абсорбер для выделения компонента C, а затем проходит n реакторов и второй абсорбер.
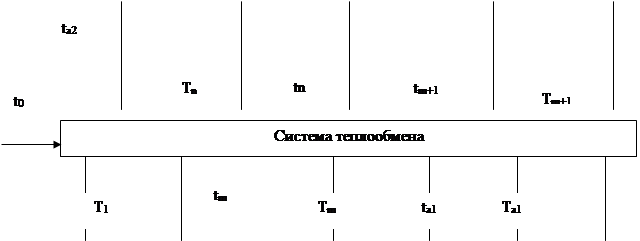
Таким образом, операторная схема выглядит следующим образом:
 |
|||||
|
|
||||
 |
|||||
![]()
|
|
|
Заданы температуры на входе в реакторы и абсорберы, объемы реакторов и абсорберов. Заданы также плотности орошения в абсорберах, температура, расход и концентрации компонентов исходной смеси.
Реакторы описываются моделями идеального вытеснения. Абсорберы описываются статистическими моделями по экспериментальным данным.
Скорость реакции в реакторе описывается уравнением:
W= (k (t) ×a×b/ (a+0,8×c)) ×(1-(c/ (Kр(t) ×a×b0,5))2),
где a, b, c – концентрации компонентов, об. доли.
При построении системы теплообмена могут использоваться пар и вода со следующими характеристиками:
начальная температура воды – 20°С,
конечная температура воды не более 90°С,
температура пара 460°С,
температура конденсации греющего пара 520 ккал/кг,
стоимость воды 0,00007 ус.д.ед./кг.
стоимость греющего пара 0,001 ус. д. ед./кг.
Коэффициенты теплопередачи:
в теплообменниках 19 ккал/(м2×ч×°С),
в нагревателях 22 ккал/(м2×ч×°С)
в холодильниках 20 ккал/(м2×ч×°С);
Теплоемкость реакционной смеси 0,33ккал/(м3×°С);
Время работы установки 8800 ч/год.
Нормативный коэффициент эффективности 0,12
Стоимостной коэффициент a 483
Вариант курсовой работы №1
m=3; n=2. Все реакторы идеального вытеснения.
| t0=60°C | t1=415°C | t2=460°C | t3=420°C |
| ta1=180°C | t4=415°C | t5=405°C | ta2=175°C |
Расход смеси на входе в систему – 120000 м3/ч.
Концентрации компонентов:
А – 0,08 об. доли;
В – 0,09 об. доли;
С – 0,0008 об. доли.
Объемы реакторов, м3:
V1=70; V2=50; V3=50; V4=60; V5=40.
Объемы абсорберов, м3:
V1=25; V2=26.
Плотность орошения в 1–_м абсорбере 18 м3/м2.
Плотность орошения во 2–_м абсорбере 18 м3/м2.
Для получения значений k0 и E в уравнении Аррениуса использовать данные таблицы 1 и МНК.
Kр (t) =10^ (4905/T-4,6455)
Для получения статистической модели абсорбера использовать данные таблицы 2 и метод Брандона.
Таблица 1. Зависимость константы скорости от температуры
| t, °C | k,1/c |
| 400 | 0,4 |
| 405 | 0,4 |
| 415 | 0,5 |
| 435 | 0,6 |
| 455 | 0,8 |
| 485 | 1,3 |
| 505 | 1,6 |
| 530 | 2,2 |
| 575 | 3,5 |
| 595 | 4,3 |
| 605 | 4,7 |
| 615 | 5,2 |
Таблица 2. Экспериментальные данные по работе абсорберов
| Номер Опыта | Твх, ˚С | Плотность орошения, м3/м2 | Объем абсорбера, м3 | Твых, ˚С | Степень абсорбции y, % |
| 1 | 170 | 13 | 22 | 65 | 72,2 |
| 2 | 180 | 14 | 25 | 57 | 78,1 |
| 3 | 170 | 13 | 30 | 49 | 84,4 |
| 4 | 160 | 18 | 21 | 56 | 85,1 |
| 5 | 188 | 17 | 27 | 49,5 | 87,9 |
| 6 | 200 | 16 | 24 | 59 | 79,0 |
| 7 | 210 | 19 | 22 | 60 | 80,5 |
| 8 | 150 | 20 | 25 | 44 | 99,9 |
| 9 | 174 | 21 | 26 | 44,5 | 98,9 |
| 10 | 182 | 21 | 26 | 45,5 | 97,15 |
| 11 | 190 | 21 | 26 | 46,5 | 95,5 |
| 12 | 170 | 18 | 26 | 47,5 | 92,43 |
| 13 | 160 | 17 | 29 | 43 | 97,19 |
| 14 | 170 | 15 | 24 | 56 | 81,5 |
| 15 | 180 | 15 | 24 | 57,5 | 80,0 |
| 16 | 190 | 15 | 24 | 59 | 78,0 |
| 17 | 210 | 15 | 24 | 62 | 75,0 |
| 18 | 225 | 16 | 22 | 62 | 72,0 |
| 19 | 210 | 18 | 29 | 48 | 90,0 |
| 20 | 150 | 18 | 19 | 59 | 83,5 |
| 21 | 186 | 14 | 25 | 58 | 77,5 |
| 22 | 190 | 14 | 25 | 59 | 77,0 |
Введение
Лежащий в основе промышленного производства химико-технологический процесс представляет собой совокупность операций, позволяющих получить целевой продукт из исходного сырья. Любое химическое производство может быть представлено в виде трех блоков: подготовки и очистки сырья, химического превращения, выделения и очистки целевых продуктов. Эти блоки связаны между собой потоками вещества и энергии. Современная химическая технология разрабатывает и изучает совокупность физических и химических процессов и оптимальные пути их осуществления и управления ими в промышленном производстве различных веществ и материалов.
Количественное описание процессов химической технологии основано на законах химической термодинамики, переноса количества движения, теплоты и массы и химической кинетики. Анализ кинетических закономерностей единичных процессов, их взаимного влияния позволяет разработать технологический режим, т.е. оптимальную совокупность параметров (температура, давление, состав исходной реакционной смеси, природа катализатора), определяющих такие условия работы аппарата или системы аппаратов, которые позволяют получить наибольший выход продукта или обеспечить наименьшую его себестоимость. Математическое моделирование, широко используемое при расчетах химических процессов и оборудования, включает формализацию процесса в виде математической записи, задание различных значений режимных параметров системы для отыскания с помощью ЭВМ значения выходных параметров и экспериментальное установление адекватности модели изучаемому объекту. Оптимизация работы агрегатов осуществляется по экономическим и энерготехнологическим показателям. Если прежде при этом стремились достичь максимального результата по одному параметру, например, получить максимальный выход продукта, то теперь требуется оптимизация, включающая учет таких параметров, как энергетические и материальные ресурсы, защита окружающей среды, обеспечение заданного качества продуктов, безопасность процессов, продуктов и отходов производства.
Современное химическое предприятие – это сложная химико-технологическая система, состоящая из большого числа аппаратов и связей (потоков) между ними. Признание факта взаимного влияния агрегатов, составляющих ХТС, привело к необходимости рассматривать технологический процесс при его проектировании на основе системного подхода, когда химическое предприятие может быть представлено в виде многоуровневой иерархической структуры.
Основные этапы создания ХТС таковы. Первый уровень заканчивается составлением математических моделей элементов подсистем ХТС. Далее переходят к решению задач анализа, синтеза и оптимизации ХТС. Анализ состоит в изучении свойств и эффективности функционирования ХТС на основе ее математической модели. Свойства системы зависят как от параметров и характеристик состояния элементов (подсистем), так и от структуры технологических связей между элементами. Естественно, что полная модель может быть рассчитана лишь после того, как синтезирована ХТС, то есть анализ не может производиться в отрыве от синтеза. Задача синтеза заключается в создании ХТС, работающей с высокой эффективностью. Для этого необходимо, прежде всего, выбрать оптимальную технологическую топологию системы, которая определяет характер и порядок соединения отдельных аппаратов в технологической схеме. Очевидно, что с синтезом ХТС тесно связана задача оптимизации, которая сводится к нахождению экстремального значения выбранного критерия эффективности (как правило, экономического) функционирования системы. Из определения задач анализа, синтеза и оптимизации ХТС видно, что все эти этапы органически связаны друг с другом.
В данной работе производился синтез ХТС, состоящей из 5 реакторов, описываемых моделями идеального вытеснения, 2 абсорберов и системы теплообмена. Для получения статистической модели абсорберов по экспериментальным данным использовался метод Брандона. Для построения оптимальной системы теплообмена использовался эвристический метод оптимизации. Для получения адекватной модели реакторов по приведенным в задании данным таблицы 1 при нахождении значений k0 и E в уравнении Аррениуса использован метод наименьших квадратов. К работе прилагается условная схема ХТС, полученная на основе приведенных ниже расчетов. В конце даются выводы о возможных путях оптимизации ХТС, полученной на основе приведенного выше задания.
1. Практическая часть
1.1 Обработка экспериментальных данных
1.1.1 Нахождение параметров уравнения Аррениуса методом МНК
Зависимость константы скорости реакции k от температуры согласно закону Аррениуса выражается формулой:
![]() , (1)
, (1)
где k0 – предэкспоненциальный множитель; e = 2,718 – основание натуральных логарифмов; Ea– энергия активации, Дж/моль; R=8,315 – универсальная газовая постоянная, Дж/(моль*К); Т – абсолютная температура,К.
Значения k0 и Ea находят, измеряя значения константы скорости k при различных температурах Т. При этом получают набор из n пар значений kiэксп и Тi. Наиболее вероятными значениями k0 и E будут такие, которые при подстановке их величин в формулу (1) дадут значения kiрасч , наиболее близкие к kiэксп .
В общем виде эта задача может быть сформулирована так: имеются две переменные x и y, связанные некоторой зависимостью f, вид которой нам известен. В эту зависимость входят некоторые постоянные a и b, значения которых нам неизвестны. При переходе к логарифмической форме уравнения (1) и заменяя y=ln(k),x=1/T,a=-E/R,b=ln(k0), имеем линейную зависимость:
![]() . (2)
. (2)
Для того, чтобы найти наиболее вероятные значения a и b, мы провели серию измерений x и y, т.е. нашли n пар значений xiэксп и yiэксп. Требуется найти такие значения a и b, которые при подстановке в зависимость (2) совместно с xiэксп дали бы значения yiрасч, наиболее близкие к yiэксп. За меру близости берут величину:
![]() . (3)
. (3)
Требуется найти минимум функции s. Это достигается решением системы уравнений
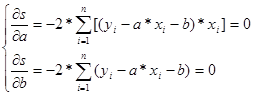 (4)
(4)
Раскрывая знаки сумм и решая систему относительно неизвестных a и b, получаем формулы для нахождения наиболее вероятных значений a и b:
 (5)
(5)
Расчет значений a и b на основе данных таблицы 1 осуществлен с использованием электронных таблиц Excel(см. Приложение 1). Полученные значения: a=-7273,034, b=9,830637.
Применяя формулы k0=exp(b), E=-R*a, получаем экспериментальные значения параметров уравнения Аррениуса:
k0=18594,79, E=60468,01 Дж/(моль*К).
Практически всегда, кроме знания величин a и b, требуется определить и их погрешности Δa и Δb с некоторой степенью достоверности α. Поскольку измерения проводились с некоторой погрешностью, то yiрасч и yiэксп будут отличаться. Этот разброс характеризуется дисперсией s0, где
![]() , (6)
, (6)
где m=2 – количество определяемых констант.
Согласно Приложению 1 ![]() =0,001621.
=0,001621.
Определение параметров a и b можно рассматривать как результат косвенных измерений. Для того, чтобы оценить точность определения параметра, можно воспользоваться законом накопления ошибок. Тогда дисперсии параметров a и b:
 , (7а)
, (7а)
 . (7б)
. (7б)
![]() =7991,043,
=7991,043,![]() =0,013721.
=0,013721.
Погрешности определения параметров a и b:
![]() , (8а)
, (8а)
![]() , (8б)
, (8б)
где t – значение критерия Стьюдента для степени достоверности α (α=0,95) и степени свободы f=n-1.
Δa=199,3,Δb=0,26.
Погрешности определяемых k0 и E: Δk0=k0*Δb=4857,21; ΔE=R*Δa=1657,36.
1.1.2 Получение статистической модели абсорбера с помощью
метода Брандона
Сложный технологический процесс можно рассматривать как многомерный объект, на который действуют вектор входных параметров X и вектор управления Z. Выходные параметры составляют вектор выходных параметров Y. Общий вид статистической модели такого объекта в векторной форме
Y=f(X,Z). (9)
Для построения статистической модели абсорберов по данным таблицы 2 использовался метод Брандона (см. Приложение 2).
Сущность метода заключается в следующем. Предполагается, что функция F(x1,x2,…,xm) в формуле (9) является произведением функций от входных параметров, т.е.
![]() , (10)
, (10)
где yрi – расчетное значение i –го выходного параметра;
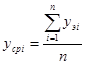 - средняя величина экспериментальных значений i – го выход-ного параметра;
- средняя величина экспериментальных значений i – го выход-ного параметра;
n – количество опытов в исходной выборке.
При использовании метода Брандона важен порядок следования функций в уравнении (10). Чем больше влияние оказывает фактор на выходной параметр, тем меньшим должен быть его порядковый номер в указанном уравнении. Поэтому задача построения модели по методу Брандона разбивается на два этапа:
1. ранжирование влияющих факторов.
2. выбор вида зависимости и построение статистической модели.
Оценить степень влияния k-го фактора на выходной параметр можно по величине частного коэффициента множественной корреляции:
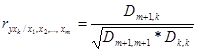 , (11)
, (11)
где ![]() - величина частного коэффициента корреляции, учитывающая влияние k-го фактора на выходной параметр y при условии, что влияние всех прочих факторов исключено; D- определитель матрицы, построенной из парных коэффициентов корреляции. Матрица имеет вид
- величина частного коэффициента корреляции, учитывающая влияние k-го фактора на выходной параметр y при условии, что влияние всех прочих факторов исключено; D- определитель матрицы, построенной из парных коэффициентов корреляции. Матрица имеет вид
![]()

Dm+1,k – определитель матрицы с вычеркнутыми m+1 строкой и k-м столбцом;
Dk,k , Dm+1,m+1 – определители матриц с вычеркнутыми k-м и (m+1)-м столбцом и строкой соответственно.
Порядок расположения влияющих факторов в уравнении (10) определяют в соответствии с убыванием величины частных коэффициентов корреляции.
В уравнении (10) каждая из функций f1(x1),f2(x2),…fm(xm) принимается либо линейной, либо нелинейной (степенной, показательной, экспоненциальной и т.д.)
Перед определением вида первой зависимости следует представить исходные экспериментальные значения выходного параметра в каждом опыте yэj в безразмерной форме yэ0j :
![]() , (12)
, (12)
где yср- средняя величина выходного параметра.
Таким образом, исходными данными для поиска первой зависимости будут нормированные значения вектора выходных параметров и опытные значения первого влияющего фактора. Поиск зависимости yр1=f1(x1) может осуществляться по-разному.
Выбрав зависимость yр1=f1(x1), определяют остаточный показатель yэ1 для каждого наблюдения:
![]() . (13)
. (13)
Предполагая, что yэ1 не зависит от x1 ,а зависит от x2,…,xm , выбирают зависимость от второго фактора. Получив расчетную зависимость yр2=f2(x2 ), находят остаточный показатель yэ2 для каждого наблюдения:
![]() . (14)
. (14)
Выполнив аналогичные действия для каждого k-го влияющего фактора, получают регрессионную зависимость для рассмотренного выходного параметра. Порядок расположения факторов для этой зависимости определен на этапе ранжирования и отличается от порядка факторов в уравнении (10). Совокупность зависимостей по каждому выходному параметру представляет собой статистическую модель многомерного технологического объекта.
Для определения адекватности модели используют оценки адекватности – корреляционное соотношение η и среднюю относительную оценку ε:
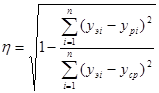 ; (15)
; (15)
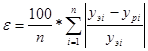 . (16)
. (16)
В данной работе для построения статистической модели абсорберов 1 и 2 применялись электронные таблицы Excel. В статистической модели имелось 3 входных параметра – Tвх, плотность орошения П и объем абсорбера Vабс. Поскольку для рассматриваемой модели имели место два выходных параметра – Твых и степень абсорбции y, требовалось получить две отдельных статистических модели.
Для построения матрицы коэффициентов парной корреляции использовалась надстройка «Анализ данных» - «Корреляция». Для нахождения определителей матриц D использовалась стандартная функция МОПРЕД(массив). После ранжирования факторов осуществлен подбор зависимостей выходных параметров от влияющих факторов, зависимости определялись с применением линий тренда на графике функций yэj=fj(xj)(выбраны зависимости, имеющие наибольшую величину досто-верности аппроксимации R^2).
Результаты:
1. Твых: результат ранжирования факторов: x1-Vабс; x2-П; x3-Твх.
f1(Vабс)=-0,001*(Vабс)^2+0,0152*Vабс+1,2384;
f2(П)=-0,0311*П+1,5259 ;
f3(Твх)=0,7074*exp(0,0019*Твх);
Твых=53,95*(-0,001*(Vабс)^2+0,0152*Vабс+1,2384)*
*(-0,0311*П+1,5259)*(0,7074*exp(0,0019*Твх)).
η=0,9802;
ε=1,9 %.
2. y: результат ранжирования факторов: x1-П; x2-Vабс; x3-Твх.
f1(П)=0,0015*П²-0,0208*П+0,9224 ;
f2(Vабс)=0,0178*Vабс+0,5546;
f3(Tвх)=-0,3571*ln(Tвх)+2,8582;
y=84,4*(0,0015*П²-0,0208*П+0,9224)*(0,0178*Vабс+0,5546)*
*(-0,3571*ln(Tвх)+2,8582);
η=0,9743;
ε=1,33 %.
Обе модели адекватно описывают процесс.
В соответствии с Заданием для абсорбера 1 определены значения входных параметров: Твх=180°C, П=18 м³/м², Vабс=25 м³. В соответствии с разработанной статистической моделью для абсорбера 1 получены значения выходных параметров: Твых=51,6°C, y=87,57.
В соответствии с Заданием для абсорбера 2 определены значения входных параметров: Твх=175°C, П=18 м³/м², Vабс=26 м³. В соответствии с разработанной статистической моделью для абсорбера 2 получены значения выходных параметров: Твых=49,2°C, y=90,02.
Полученные значения выходных параметров использовались для расчета абсорберов и для построения системы теплообмена.
1.2 Математическое описание аппаратов
1.2.1 Реакторы идеального вытеснения
Для получения достоверных данных о протекающем процессе требуется, очевидно, определить степень влияния различных факторов (гидродинамический режим, температура, давление и т.д.) на протекающий в данном аппарате химический процесс. Для описания непрерывных химических процессов используются модели химических реакторов идеального вытеснения (РИВ) и идеального смешения (РИС).
Модель идеального вытеснения характеризуется так называемым поршневым движением потока – продольное перемешивание в аппарате отсутствует, поперечное перемешивание в слоях полное. Такая модель удовлетворительно описывает, например, многие процессы в длинных трубах, особенно заполненных зернистыми слоями. В аппаратах РИВ в ходе процесса концентрация реагентов (а следовательно, и движущая сила) монотонно снижается; одновременно уменьшается скорость процесса, а также производительность аппарата. Соответственно, для реакций, протекающих в РИВ, математическое описание представляет собой систему обыкновенных дифференциальных уравнений. В общем виде уравнение материального баланса может быть записано следующим образом:
![]() , (17)
, (17)
где ri – скорость реакции по j-му реагенту в данный момент времени.
Для нашего случая система уравнений материального баланса будет иметь вид:
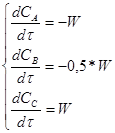 . (18)
. (18)
Поскольку в нашем случае протекает экзотермическая реакция, то систему необходимо дополнить уравнением теплового баланса, учитывающим изменение температуры во времени:
![]() , (19)
, (19)
где ![]() - коэффициент адиабатического разогрева, К;
- коэффициент адиабатического разогрева, К;
q – тепловой эффект реакции, ккал/кмоль;
Cp – мольная теплоемкость реакционной смеси, ккал/(кмоль*К).
Для решения данной системы необходимо определить начальные условия. В данном случае ими являются концентрации компонентов А,В и С, а также температура Т на входе в реактор (τ=0). Поскольку требуется определить концентрации компонентов и температуру на выходе из реактора, заранее определяется время нахождения реакционной смеси в реакторе (время контакта). Для РИВ время контакта в i-м реакторе определяется по формуле:
![]() , (20)
, (20)
где Vi – объем i-го реактора, м³;
Wi – объемный расход реакционной смеси на входе в i-й реактор, м³/с.
В данной работе решение системы проводилось с помощью метода Рунге–Кутта (использовался программный продукт Mathcad 2001 Professional и стандартная функция rkfixed). Определялись концентрации компонентов и температура на выходе из реакторов, проводилась корректировка объемного расхода реакционной смеси после каждого реактора (поскольку в результате реакции объем смеси уменьшался). Расчеты реакторов велись совместно с расчетом абсорберов, поскольку значения расхода и концентраций компонентов на выходе из 3-го реактора были необходимы для расчета 1-го абсорбера, и т.д. Данные по реакторам, полученные в результате расчетов, сведены в таблицу 3.
Таблица 3. Результаты расчета РИВ
| № реактора | V, м³ |
Объемный расход смеси на входе в реактор, м³/ч | Твх, К |
Концентрации компонентов, об.доли | Твых, К |
|||||
| На входе в реактор | На выходе из реактора | |||||||||
| А0 | В0 | С0 | А | В | С | |||||
| 1 | 70 | 120000 | 688 | 0,08 | 0,09 | 0,0008 | 0,021 | 0,06 | 0,06 | 858 |
| 2 | 50 | 115800 | 733 | 0,021 | 0,06 | 0,06 | 0,007013 | 0,053 | 0,074 | 773,1 |
| 3 | 50 | 114900 | 693 | 0,007013 | 0,053 | 0,074 | 0,00373 | 0,051 | 0,077 | 702,4 |
| 4 | 60 | 106900 | 688 | 0,004 | 0,055 | 0,01 | 0,0002584 | 0,053 | 0,014 | 698,7 |
| 5 | 40 | 106700 | 678 | 0,0002584 | 0,053 | 0,014 | 0,0001597 | 0,053 | 0,014 | 678,3 |
Как видно из таблицы 3, смесь реагирует достаточно хорошо в 1-м и 2-м реакторах, а в 5-м реакторе почти не реагирует. Данный факт обуславливается чрезвычайно малой концентрацией компонента А в смеси, поступающей в аппарат. В то же время в конечной смеси, выходящей из 5 –го реактора, высока концентрация В, что указывает на недостаток компонента А в исходной смеси.
1.2.2 Абсорберы
В абсорберах происходит поглощение (абсорбция) компонента С из газовой смеси жидким поглотителем (абсорбентом). Процесс абсорбции может быть описан с помощью уравнений массообмена. Однако, поскольку в п. 1.1.2. была получена статистическая модель абсорберов и определены выходные параметры – Твых и степень поглощения y, в расчетах абсорберов 1 и 2 мы пользовались ею. Расчет абсорберов велся совместно с расчетом реакторов, что обусловлено причинами, приведенными выше. Результаты расчета абсорберов приведены в таблице 4.
Таблица 4. Результаты расчета абсорберов.
| Параметр | Абсорбер 1 | Абсорбер 2 |
| Vабс, м³ | 25 | 26 |
| Плотность орошения, м³/м² | 18 | 18 |
| Твх, °C | 180 | 175 |
| Объемный расход смеси на входе в абсорбер, м³/ч | 114600 | 106700 |
Концентрации компонентов на входе в абсорбер, об.доли А В С |
0,00373 0,051 0,077 |
0,0001597 0,053 0,014 |
| Твых, °C | 51,6 | 49,2 |
| Степень абсорбции y | 0,8757 | 0,9002 |
Концентрации компонентов на выходе из абсорбера, об. доли А В С |
0,004 0,055 0,01 |
0,0001617 0,054 0,001415 |
| Количество отделенного компонента С, кмоль/ч | 344,97 | 60,014 |
Как видно из таблицы 4, абсорбер 1 работает достаточно хорошо, а для абсорбера 2 характерна низкая производительность. Отчасти это объясняется причинами, указанными в п. 1.2.2.
1.3 Синтез оптимальной тепловой системы с помощью
эвристического метода
Задача синтеза систем теплообмена формулируется следующим образом. Пусть имеется m горячих и n холодных потоков, которые мы будем называть основными технологическими потоками. для каждого из этих потоков заданы начальные температуры ![]() , конечные температуры
, конечные температуры ![]() и значения водяных эквивалентов
и значения водяных эквивалентов ![]() . Под водяным эквивалентом будем понимать произведение теплового расхода на удельную теплоемкость. Необходимо определить структуру технологических связей между теплообменными аппаратами заданного типа, а также площади поверхности теплообмена каждого аппарата, которые обеспечивали бы заданные начальные и конечные температуры основных технологических потоков при минимальном возможном значении приведенных технологических затрат Зпр, связанных с эксплуатацией синтезированной тепловой системы.
. Под водяным эквивалентом будем понимать произведение теплового расхода на удельную теплоемкость. Необходимо определить структуру технологических связей между теплообменными аппаратами заданного типа, а также площади поверхности теплообмена каждого аппарата, которые обеспечивали бы заданные начальные и конечные температуры основных технологических потоков при минимальном возможном значении приведенных технологических затрат Зпр, связанных с эксплуатацией синтезированной тепловой системы.
Синтезируемую тепловую систему можно разделить на две подсистемы: внутреннюю (рекуперативную), где в теплообмене участвуют только основные технологические потоки, и внешнюю, где при теплообмене используются вспомогательные технологические потоки. При этом внешняя подсистема используется только тогда, когда во внутренней подсистеме не удается получить заданные конечные температуры.
Приведенные технологические затраты, связанные с эксплуатацией синтезируемой тепловой системы, могут быть выражены следующим образом:
![]() , (21)
, (21)
где З1 – затраты на рекуперативные теплообменники, ус.д.ед.;
З2 – затраты на вспомогательные теплообменники, ус.д.ед.;
З3 – затраты на вспомогательные теплоносители, ус.д.ед.;
Ен – нормативный коэффициент эффективности.
Если во внутренней подсистеме используется k1 теплообменных аппаратов, а во внешней l1 , то
![]() , (22)
, (22)
где Ц – стоимость теплообменника.
При расчете i-го теплообменника любой подсистемы используется формула:
![]() , (23)
, (23)
где Fi – площадь поверхности теплообмена i-го теплообменника, м²;
a – стоимостной коэффициент, зависящий от типа теплообменника.
Затраты на вспомогательные теплоносители определяются по формуле:
![]() , (24)
, (24)
где θ – продолжительность годовой эксплуатации системы, ч/год;
Цp – стоимость p-го вспомогательного теплоносителя в p-м вспомогательном теплообменнике, ус.д.ед./кг;
Gpl – расход p-го вспомогательного теплоносителя в l-м вспомогательном теплообменнике, кг/ч;
p1,l1- число вспомогательных теплоносителей и теплообменников соответственно.
При синтезе тепловой системы используются следующие формулы:
![]() , (25)
, (25)
где Q – тепловая нагрузка теплообменника, Вт;
K – коэффициент теплопередачи, Вт/(м²*К);
Δtср – средняя разность температур, К.
Тепловая нагрузка теплообменника или количество тепла, переданное в одном аппарате, определяется на основе концепции передачи максимально возможного количества тепла при минимально допустимой разности температур на концах теплообменника:
если ![]() , то теплообмен невозможен;
, то теплообмен невозможен;
если ![]() , то
, то ![]() ;
;
если ![]() , то
, то ![]() .
.
![]() , (26а)
, (26а)
![]() , (26б)
, (26б)
![]() , (26в)
, (26в)
![]() , (27а)
, (27а)
![]() . (27б)
. (27б)
Задача синтеза тепловой системы решается путем формирования множества возможных комбинаций исходных горячих потоков и холодных потоков для проведения физически реализуемых операций теплообмена в теплообменном аппарате. Для этой цели строят таблицу пар взаимодействующих потоков, исходя из условия Q→max. Из таблицы пар выбирается пара потоков, вступающих во взаимный теплообмен. Если в результате теплообмена данные потоки достигли заданных конечных температур, то они исключаются из рассмотрения. Иначе, начальным температурам этих потоков присваиваются значения конечных температур результирующих потоков, после чего таблица пар перестраивается, и выбирается новая пара потоков. Данная операция производится до тех пор, пока не останется потоков, способных вступать во взаимный теплообмен, или все потоки достигнут требуемых конечных температур.
При необходимости для достижения заданных конечных температур в теплообменных системах используются вспомогательные тепло- и хладагенты.
Таким образом, задача синтеза является многоэтапной задачей, в которой на каждом этапе осуществляется выбор пары потоков, вступающих во взаимный теплообмен. Пары потоков можно выбирать с помощью эвристических правил (эвристик). Под эвристиками понимают правила, полученные на основе анализа опыта квалифицированных специалистов, которые носят характер вероятных, хотя и не всегда безошибочных утверждений.
В данной работе использовались следующие эвристики:
1. Выбрать вариант теплообмена между потоками i и j, для которых начальные температуры максимальны.
2. Выбрать вариант теплообмена между потоками, который обеспечивает максимальное количество передаваемого тепла.
Выбор конкретной эвристики на каждом этапе синтеза осуществлялся с помощью равномерно распределенных в интервале [0,1] псевдослучайных чисел. Если выбранное псевдослучайное число А входило в интервал [0;0,5], то выбиралась 1-я эвристика, если оно входило в интервал [0,5;1], то выбиралась 2-я эвристика.
Синтез тепловой системы осуществлялся с применением электронных таблиц Excelна основе Задания и таблицы 3. Таблица исходных потоков приведена в таблице 5.
Таблица 5. Основные технологические потоки
| Холодные потоки | Горячие потоки | ||||||
| № | tхн, К | tхк, К | W, кВт/К | № | tгн, К | tгк,К | W, кВт/К |
| 1 | 333 | 688 | 46,024 | 1 | 858 | 733 | 44,413 |
| 2 | 773,1 | 693 | 44,068 | ||||
| 3 | 702,4 | 453 | 43,953 | ||||
| 2 | 324,6 | 688 | 41 | 4 | 698,7 | 678 | 40,923 |
| 5 | 678,3 | 448 | 40,923 | ||||
Разработанная тепловая система имеет следующий вид:
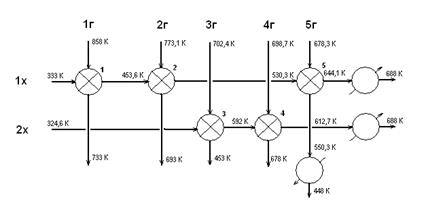
Площади поверхности теплообмена аппаратов приведены ниже.
1. Теплообменник 1: F=625,2 м² .
2. Теплообменник 2: F=663,1 м².
3. Теплообменник 3: F=4165 м².
4. Теплообменник 4: F=445,9 м².
5. Теплообменник 5: F=8967,9 м².
6. Холодильник: F=1055,7 м².
7. Нагреватель 1: F=1225,5 м².
8. Нагреватель 2: F=1578 м².
Приведенные затраты, связанные с эксплуатацией синтезированной тепловой системы составили 148919,3 ус.д.ед./год.
Выводы
В данной курсовой работе был проведен синтез ХТС с использованием различных методов обработки экспериментальных данных, а также принятых математических моделей аппаратов (РИВ). Синтез тепловой системы осуществлялся с помощью эвристического метода.
Расчеты реакторов РИВ показали, что равновесие в 1-м реакторе наступает достаточно быстро, и почти половина объема реактора не работает. Поэтому целесообразно было бы уменьшить объем 1-го реактора до V=45 м³, что привело бы к существенной экономии материалов. Среди недостатков данной ХТС можно указать также крайне низкую эффективность работы реакторов 4 и 5, а также абсорбера 2, что, в свою очередь, связано с низкой концентрацией компонента А в реакционной смеси и связанными с ней низкими скоростями процесса в реакторах и малым содержанием целевого компонента С в смеси, поступающей во 2 абсорбер. В то же время в смеси, выходящей из абсорбера 2, велико содержание компонента В, что весьма нежелательно. Устранить эти недостатки можно, увеличив концентрацию компонента А в свежей реакционной смеси либо обеспечив рециркуляцию реакционной смеси, содержащей избыток В с добавлением в нее свежих компонентов А и В до нужной концентрации, указанной в Задании.
Список используемой литературы
1. Саутин С.Н., Шибаев В.А., Левин В.Л. Исследование на ЭВМ кинетических закономерностей химических реакций. Метод. указ. - Л.: ЛТИ им. Ленсовета, 1988.
2. Холоднов В.А., Вениаминова Г.Н., Иванова Е.Н., Чепикова В.Н. Программные продукты MicrosoftOffice в химии и химической технологии. Обработка экспериментальных данных с использованием электронных таблиц Excel. Метод указ. – СПб.: СПГТИ(ТУ), 2002.
3. Кузичкин Н.В., Саутин С.Н., Холоднов В.А., Хартманн К. Синтез оптимальных тепловых систем. Метод. указ. – Л.: ЛТИ им. Ленсовета, 1985.
4. Химическая энциклопедия. В 5-и т.Тт.4,5/гл. ред. Зефиров. – М.: Изд-во «Большая Российская энциклопедия», 1995-1998.