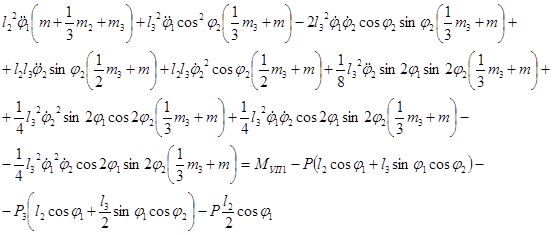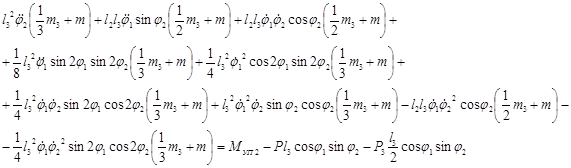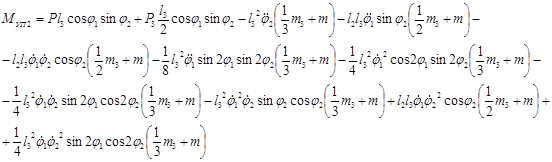| Скачать .docx |
Реферат: Контрольная работа: Кинетическая энергия манипулятора
КИНЕМАТИКА
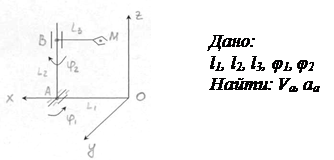
I Определить скорость и ускорение точки М методом простого движения точки
Составим уравнения точки М
Определим проекции скорости точки М на оси координат
Квадрат модуля скорости точки М вычислим по формуле:
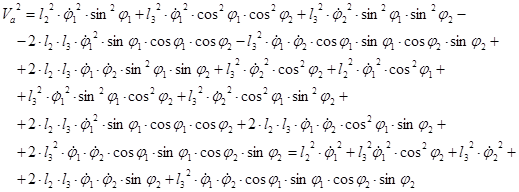
Определим проекции ускорения точки М на оси координат
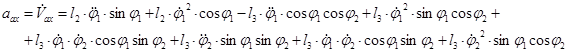
Модуль ускорения точки М
II Определить скорость и ускорение точки М методом сложного движения точки
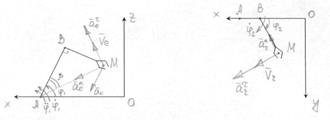
По теореме о сложении скоростей имеем:
;
;
По методу проекции имеем:
По теореме о сложении ускорений имеем:
По методу проекции имеем:
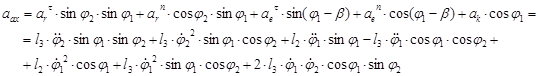
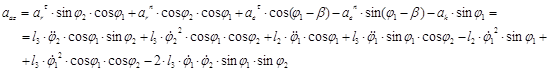
Модуль ускорения точки М
СТАТИКА
Дано:
| φ1 =-30 |
Fx =4 H |
l1 =0,6 м |
S0 =1 см2 |
| φ2 =-75 |
Fy =6 H |
l2 =0,6 м |
ρ(стали) =7,8 г/см3 |
| Fz =2 H |
l3 =0,4 м |
g=10 м/с2 |
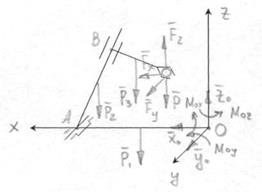
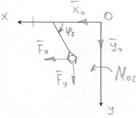
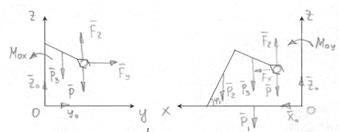
Рассмотрим равновесие всего манипулятора
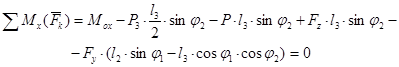
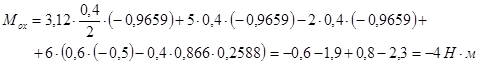
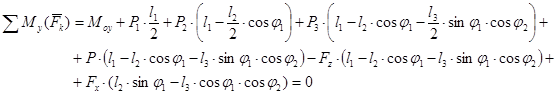
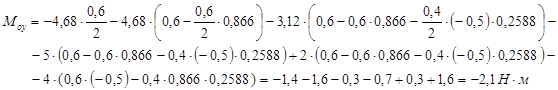
Рассмотрим равновесие руки манипулятора
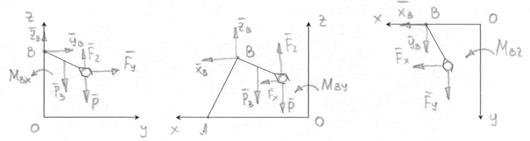
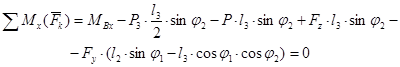
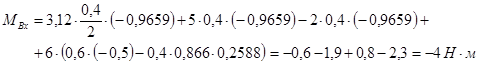
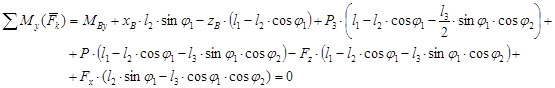
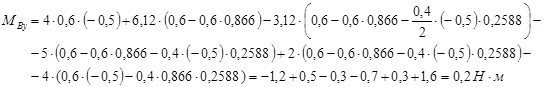
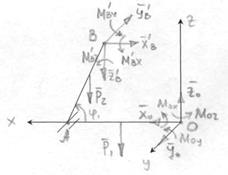
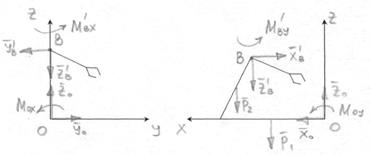
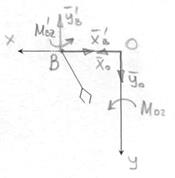
Рассмотрим равновесие без руки манипулятора
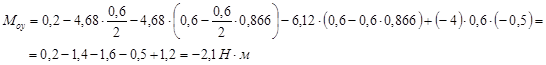
ДИНАМИКА
Дано:
| l1 =0,6 м |
m1 =0,468 кг |
t=2c |
| l2 =0,6 м |
m2 =0,468 кг |
|
| l3 =0,4 м |
m3 =0,312 кг |
|
| g=10 м/с2 |
m=0,5 кг |
n =2 – число степеней свободы
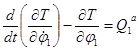- Уравнения Лагранжа 2 рода
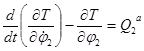
Определим кинетическую энергию манипулятора
, т.к. первая деталь манипулятора неподвижна
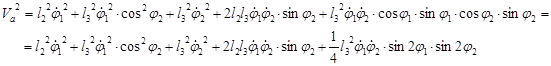
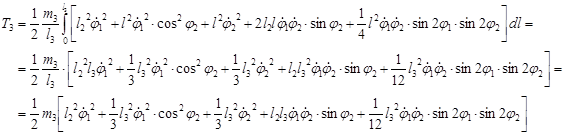
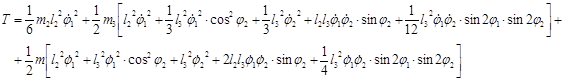
Вычисляем частные производные
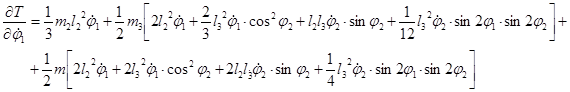
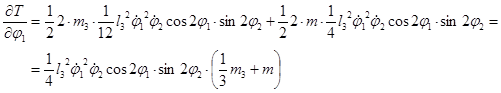
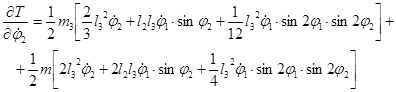
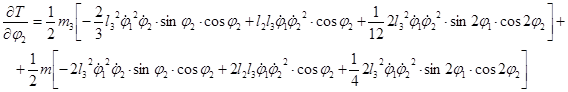
Вычисляем обыкновенные производные по времени
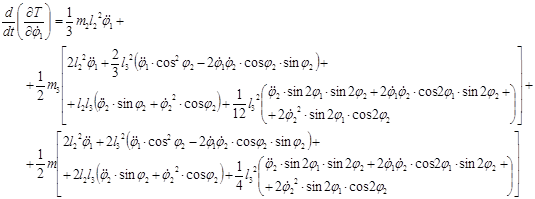
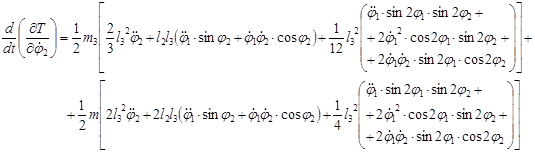
Для определения обобщенных сил сообщаем системе возможные перемещения
Активные силы: МУП1, МУП2, Р1, Р2, Р3, РМ .
1) 
2) 
Подставляем преобразованные выражения в уравнения Лагранжа 2 рода
