Реферат: Задача по Физике

1. С помощью принципа возможных перемещений (общего уравнения динамики) определить ускорение центра масс тела А.

2. С помощью принципа Даламбера найти натяжение нити на всех участках. Рассмотрев динамическое равновесие последнего тела, сделать проверку правильности выполненных расчётов.

3. Составить дифференциальное движение Лагранжа и определить ускорение центра масс тела А. Сравнить результат.

4. Найти расстояние S, пройденное центром масс тела А за время t₁ = 2 с, и скорость его в этот момент времени.

5. С помощью теоремы об изменении кинетической энергии системы определить скорость центра масс тале А в момент t, когда он пройдёт расстояние S, найденное в п. 4.

Р = 30 Н, G = 15 HF = 20Н, М=300 Нсм R= 0,3 м, r= 0,2 м, g= 10м/с.

Решение.

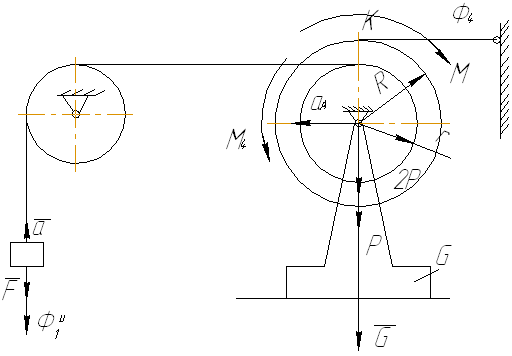
Рисунок 1

1. Общее уравнение динамики для системы запишется как

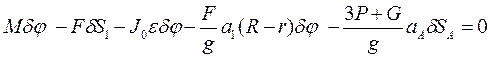
(1)

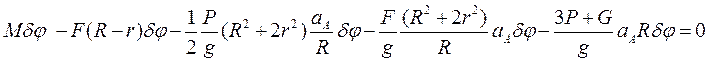
Сократив на dj, получим

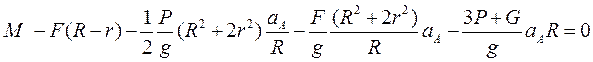
Или можно записать

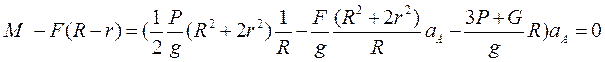
Откуда найдём ускорение

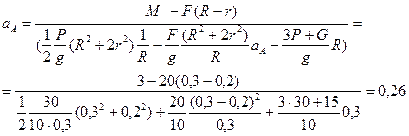м/с (2)

2. Уравнение Лагранжа II рода. Система имеет одну степень свободы, тодга

, (2)

где Qx – обобщённая сила,

Т –кинематическая энергия системы;

q– обобщённая координата

Т=Т₁ +Т₂ +Т₃

Кинематическая энергия основания, вокруг которого вращается ступенчатый цилиндр

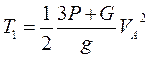
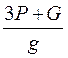- масса основания

Момент инерции цилиндра относительно оси вращения

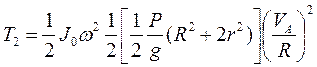
Где - момент инерции цилиндра относительно оси вращения

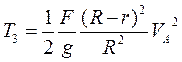
Теперь окончательно запишем кинематическую энергию системы

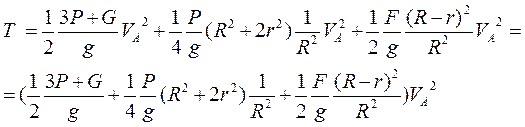(3)

Частная производная

Где 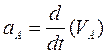(q=S) – обобщённая координата

Найдём обобщённую силу

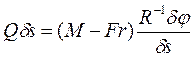откуда

Откуда получим окончательное уравнение

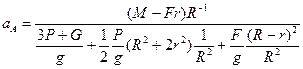(4)

Сравнив выражения (2) и (4) видим, что они полностью идентичны

Ускорение а_А =0,26 м/с найдено верно.

3. Найдём расстояние S, пройденное телом А за время t= 2 с. Так как, движение ускоренное тела А (это груз 1) и начинается из состояния покоя, то скорость его при t= 2 с будет

м/с

А путь пройденный телом А будет

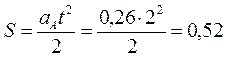м

4. Используя теорему об изменении кинематической энергии системы

(3)

Так как движение начинается из состоянии покоя, то То=0. А так как система снабжена идеальными связями, то работа внутренних сил . Следовательно (3) запишем как

(6)

где - работа внешних сил и

Работа внешних сил и будет равна,

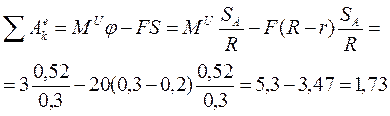Дж

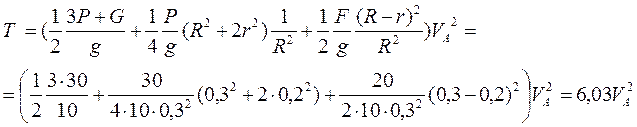
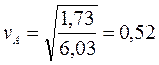м/с, что совпадает с ранее полученным значением

5. Натяжение нитей

а) Рассмотрим в равновесии груз 1. К нему приложены силы , и , где - сила натяжении нити, удерживающей груз 1.Спроецируем сумму сил на ось х

-- += 0 или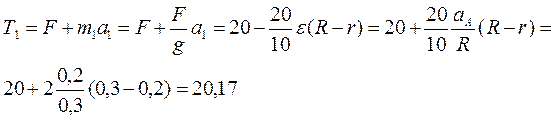

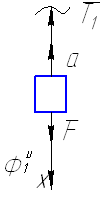
Рисунок 2

б) Рассмотрим в равновесии ступенчатый цилиндр. Составим уравнение равновесия сил относительно оси О

(4)

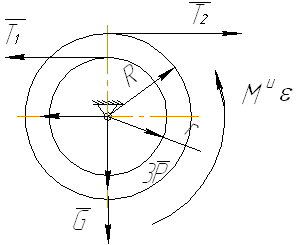
Рисунок 3

Откуда

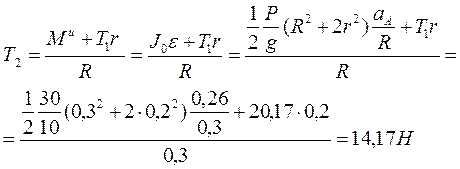Н