| Скачать .docx |
Курсовая работа: Сопромат
Задача № 1
Тема: Расчет на прочность статически определимых систем при растяжении и сжатии
Требуется:
1. Построить эпюру продольного усилия Ni
2. По условию прочности подобрать размер поперечного сечение «а», если 
=160 МПа
3. Для рассчитанного размера поперечного сечения построить эпюру нормальных напряжений 
4. Построить эпюру осевых перемещений W и найти наибольшую величину относительных деформаций 
, если 
5. Определить потенциальную энергию упругих деформаций U
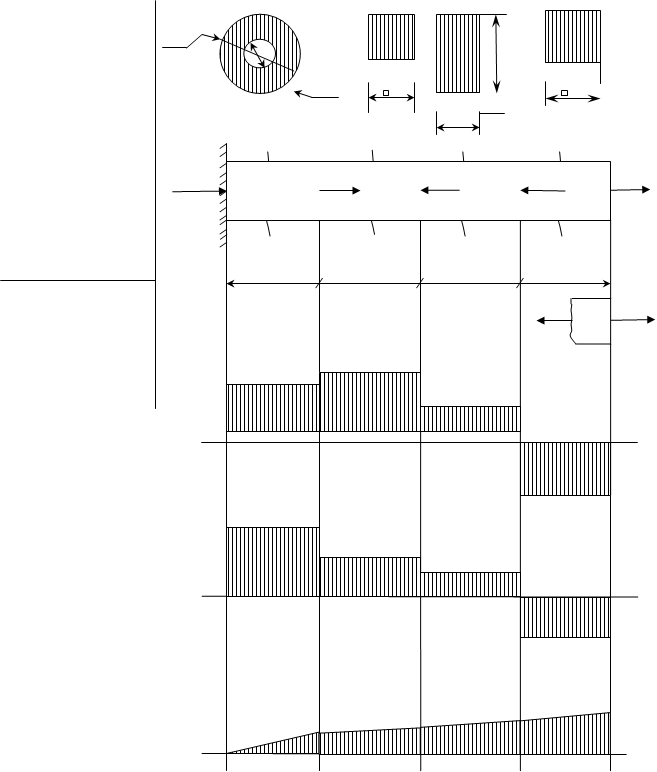Дано: 7
Р1 = 50 кН; l 1 = 3 м ; Ø a 2a
Р 2 =65 кН ; l2 = 2 м ; Ø2a a 2a
Р 3 =40 кН ; l3 = 3 м ; a
Р4 =10 кН; l 4 = 1м ; D C B A
Формы сечения: Ra P4 P3 P2 P1
А1 № 11 А3 № 4
А2 № 9 А4 № 7 IV III II I
l 1 l2 l3 l4
Ni
= ? ; = ? ; 
= ?; N1
P1
= ? ; “a
” = ? ; 45 55
15
+ Эп.N (kH)
-
16 50
3,69 2
+ Эп.σ(МПа)
-
13
1,99 2,986 3,534 6,9
0
Эп.∆l (мм) +
Решение:
Определяется сила реакции опор RА из уравнения статики:
 |
Делим на 4 участка, обозначая их римскими цифрами (I, II, III, IV), а также характерные сечения через заглавные буквы (А, В, С, D, Е).
Определяется продольная сила на каждом участке методом сечения:
Строится эпюра продольных сил Ni
Определяется площадь поперечных сечений на каждом участке
А1=а*а=а2
А2=2а*а=2а2
А3=2а*2а=4а2
Определяется нормальное напряжение на каждом участке через 1/а2
Определяется максимальное значение нормального напряжения, не превышающее допускаемого напряжения, равное 160 МПа: 
Максимальное значение напряжения на третьем участке 
Находится значение «а»:
Принимается а = 19,4мм
Определяются действительные значения площадей поперечных сечений:
Определяются истинные значения нормального напряжения на каждом участке:
10. Строится эпюра нормального напряжения
11. Определяется относительная продольная деформация на каждом участке:
, где Е = 2 105МПа
12. Определяется относительная продольная деформация по сечениям:
13. Определяется относительное удлинение 
и строится эпюра этих значений (Рис 1д):
Определяется максимальное значение относительного удлинения: 
14. Определяется удельная потенциальная энергия
15. Определяется полная удельная потенциальная энергия
16. Определяется относительная погрешность нормального напряжения:
Задача №2
Тема: Расчет на прочность статически неопределимых систем при сжатии и растяжении
Дано:
Схема бруса
Размеры и нагрузки
Материал брусьев – сталь 3
Допускаемое напряжение 
Модуль продольной упругости 
Требуется:
Определить допускаемую нагрузку для ступенчатого бруса
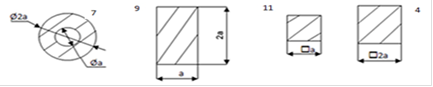
Дано:
l = 30 см = 0,3 м = 300 мм
А = 10 см2
=
К = 0,15
[Р] = ?
Эп. N ( kH ) Эп. σ ( kH ) Эп. l (мм)
Ra
+ - + - + -
A A
1.5l 3A I 255 53
0,02
B 2A II 133 В
l 0,047
C
C 425 С
1.5l 4P 4A III 66,4 0,066
D
D
l A IV 255 159
E 0,035
E
∆ R e
Решение:
Составляется уравнение статики
Составляется уравнение совместности деформации УСД:
- от заданных сил
- УСД (1)
Определяются продольные силы на каждом участке:
=? когда нет RE
Находим относительное удлинение на каждом участке
Определяется 
- относительное удлинение силы реакции опор, когда нет сил Р и 2Р:
Подставляем значения и в уравнение (1)
Подставляем значение силы 
в уравнение статики 
Определяем значения продольных сил, подставляя значения 
Определяется значение нормального напряжения на каждом участке 
Находим максимальное значение нормально напряжения
Принимаем Р = 170 кН
Определяются действительные значения продольных сил:
10. Определяются истинные значения нормального напряжения на каждом участке 
:
Находим относительное удлинение 
Находим относительное удлинение по сечениям 
Определяем относительное удлинение 
По заданной формуле вычисляем значение зазора 
, оно должно соответствовать значению 
Проверка
Задача № 3
Тема: Расчет на прочность статически неопределимых систем при растяжении и сжатии.
Требуется:
Найти усиление и напряжение в стержнях, выразив через силу Р1
Определить допускаемую нагрузку [Р], если [σ] = 160 МПа
Найти предельную нагрузку Рпр, если [σ1] = 240 МПа и h1 = 1,5
Сравнить величины допускаемых нагрузок Рпр и Р, для чего найти их отношения.
 |
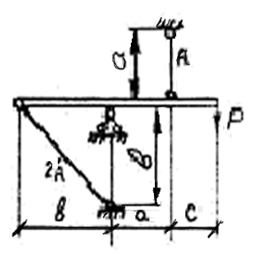
Дано:
А=14см2 = 14·10 - 4м
а=2,3м
в=2,7см
с=1,7см
[σ] =160 МПа
hТ = 1,5
 |
Найти: Р=?, РТ =?, [РТ] =?
Решение.
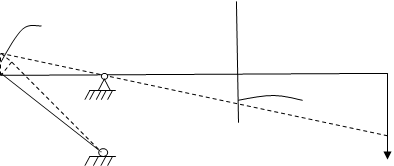
1. Составляется уравнение статики для стержневой системы
1. Σ Мi = 0; Ν1·a-P(a+c) +N2cos 45·b =0
2. Σ Zi =0; Z0 +Ν2· cos45 = 0
3. Σ Yi =0; Y0 + Ν1– P - N2·cos 45 = 0
В три уравнения равновесия входят четыре неизвестные силы, и, следовательно, задача является статически неопределимой. Для составления уравнения рассмотрим деформацию конструкции.
2. Рассмотрим подобие двух треугольников 
;
Рассмотрим 
для нахождения деформации системы.
OB=b OA=a
y0
N1
В
N2
Р P 
 |
|
 |
B1 ∆l1
B2 O A
B A1 ∆l2
3. Подставляем 
в уравнение моментов и выражаем их через Р
4. Находим значения нормальных напряжений σ1, σ2
σ1 = 
σ1 = 
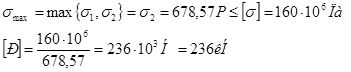
Принимаем 
5. Находим действительные значения Ni
6. Находим действительные значения σi
σ1 = 
=678,57
=160МПа
σ2 = 
=339,29=79,7МПа
7. Определяем предельную нагрузку Pпр, исходя из условия равновесия
Σ Мi = 0; Ν1·а– Р·(a+c) + N2cos 45·b =0, где N1 = σт · А, и N2 = σт · 2А; σт=240МПа
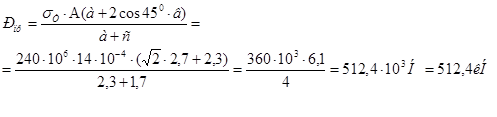
8. Находим предельно допускаемую нагрузку
Задача № 4
Тема: Расчет статически определимых брусьев на прочность и жесткость при кручении.
Дано:
Схема бруса.
Размеры нагрузки.
Требуется:
Рассчитать брус на прочность и жесткость
Построить эпюры крутящих моментов, касательных напряжений и углов поворота.
 |
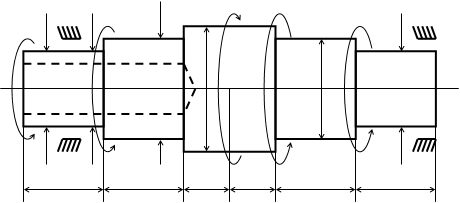Дано:
m1 = 400 Н∙м
m2 = 1200 Н∙м
m3 = 2400 Н∙м
m4 = 400 Н∙м
m5 = m5 Н∙м
[τ] = 40 МПа
[θ] = 0,5 
d = 0,5
d1 = 1.5b
d2 = 2b
d3 = 2.5b
a = 0.3 м
Найти: Т, τ, θ - ?
Решение.
Составим уравнение статики:
Σ Мi = 0
m1 – m2 – m3 + m4 + m5 = 0
m5 = - m1 + m2 + m3 – m4 = - 400 + 1200 + 2400 – 400 = 2800 H·м
T1 = + m1 = 400 H·м
T2 = m1 – m2 = 400 – 1200 = - 800 H·м
T3 = m1 – m2 – m3 = - 800 – 2400 = - 3200 H·м
T4 = m1 – m2 – m3 = - 800 – 2400 = - 3200 H·м
T5 = m1 – m2 – m3 + m4 = – 2800 H·м
T6 = m1 – m2 – m3 + m4 + m5 = 0 H·м
Определяем полярный момент сопротивления на каждом участке Wpi:
Определяется касательное напряжение на каждом участке по формуле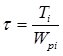 
, выражая каждое значение через 1/b3
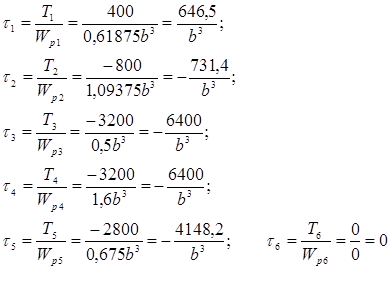
Определяем максимальное значение касательного напряжения из пяти значений:
τmax = max {τ1, τ2, τ3, τ4, τ5} ≤ [τ] ;
τ3 ≤ [τ]
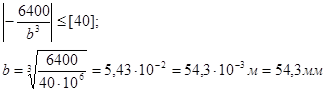
Определяется полярный момент инерции по данной формуле 
на каждом участке:
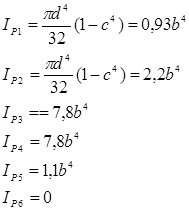
5. Определяем относительный угол закручивания по формуле
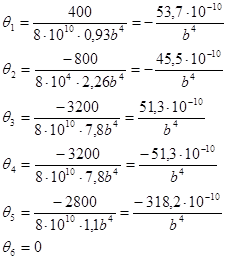
Определяем максимальное значение:
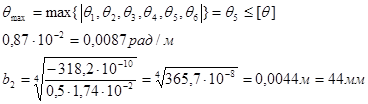
Примем максимальное значение из полученных значений b:
b≥{|b1|,|b2|} = b1 = 54,3 мм = 54,3·10 - 3 м = 55мм
6. Определяем действительные значения касательного напряжения τi:
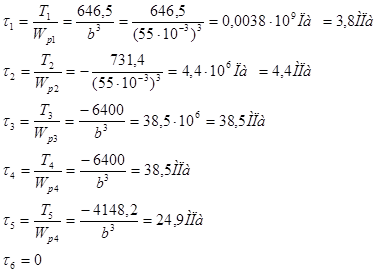
Определяем действительные значения относительного угла закручивания θi:
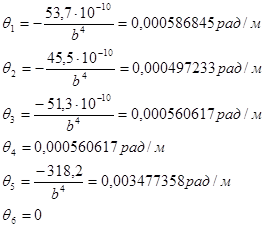
Определяем по формуле значение перемещения
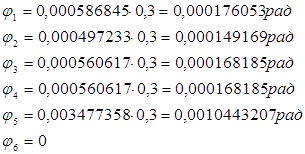
Находим числовые значения перемещения Δφi по сечениям:
φА = 0
φВ = φА + φ1 = 0 + 0,000176053 = 0,000176053 рад;
φС = φВ + φ2 = 0,000176053 + 0,000149169 = 0,000325222 рад;
φD = φС + φ3 = 0,000325222 + 0,000168185 = 0,000493407 рад;
φЕ = φD + φ4 = 0,000493407 + 0,000168185 = 0,000661592 рад;
φF = φЕ + φ5 = 0,000661592 + 0,003477358 = 0,00413895 рад;
φG = φF + φ6 = 0,00413895 + 0= 0,00413895 рад.