| Скачать .docx |
Реферат: Обработка результатов эксперимента 2
Обработка результатов эксперимента
Определения
Измерение – нахождение значения физической величины опытным путём с помощью специально для этого предназначенных технических средств.
Измерение состоит из наблюдений и выполнения математических операций по определению результата измерения.
Наблюдение – измерительная (экспериментальная) операция по нахождению значения физической величины, подлежащего дальнейшей обработке совместно с результатами других подобных операций.
Прямое измерение – измерение, при котором измерительный сигнал, поступающий на вход средств измерения, содержит информацию о самой измеряемой величине.
Косвенное измерение – измерение, при котором искомое значение физической величины получают в результате вычислений на основании её зависимости от величин, измеряемых прямо.
Погрешность результата измерения – отклонение результата измерения от истинного значения измеряемой физической величины.
![]() – абсолютная погрешность результата измерения;
– абсолютная погрешность результата измерения;
![]() – относительная погрешность результата измерения.
– относительная погрешность результата измерения.
Здесь X – измеренное значение физической величины, X 0 – истинное значение физической величины.
Систематическая погрешность – при повторных наблюдениях остаётся постоянной или изменяется закономерным образом.
Случайная погрешность – проявляется в хаотическом изменении результатов повторных наблюдений, проводимых одними и теми же средствами измерений одним и тем же экспериментатором.
Приборная погрешность – погрешность измерительного прибора (средства измерения), определённая при его испытаниях и занесённая в его паспорт.
Класс точности прибора (средства измерения) – характеристика прибора, выраженная пределами его основной и дополнительной погрешностей.
Класс точности указывается на шкале прибора в виде числа, заключённого в кружок, либо просто числа .
1. Класс точности g – число в кружке – обозначает максимальную относительную погрешность результата измерения, выраженную в процентах.
Если X – отсчёт величины по шкале прибора, то приборная погрешность (её абсолютное значение) равна
![]()
2. Если класс точности g – просто число, то приборная погрешность равна
![]()
где К – максимальное показание шкалы прибора.
Если класс точности прибора не указан, то приборная погрешность принимается равной половине цены деления шкалы. Если прибор цифровой, то приборная погрешность равна ± единице счёта . При наличии у прибора нониуса погрешность такого прибора принимается равной одному делению шкалы нониуса.
Случайные погрешности
Принято считать, что случайные погрешности измерений распределяются по нормальному закону (закону Гаусса) :
1. Погрешности могут принимать непрерывный ряд значений.
2. При большом числе наблюдений погрешности равных значений, но разных знаков встречаются одинаково часто.
3. Частота появления погрешностей уменьшается с увеличением значения погрешностей (большие по абсолютному значению погрешности встречаются реже, чем малые).
Аналитически закон распределения Гаусса описывается выражением
![]() ,
,
где s – параметр распределения, равный полуширине гауссовой кривой на уровне 0.607 от её максимального значения, ![]() – погрешность наблюдения с порядковым номером i
, X
i
– результат того же наблюдения.
– погрешность наблюдения с порядковым номером i
, X
i
– результат того же наблюдения.
Считая, что проведено бесконечно большое число наблюдений N , просуммируем погрешности наблюдений:
![]()
Т.к. погрешности равных значений, но разных знаков при гауссовом распределении встречаются одинаково часто, то
![]()
В свою очередь
![]()
Следовательно,

![]()
т.е. при абсолютно точном средстве измерения и бесконечно большом числе наблюдений (N ®¥) среднее значение измеряемой физической величины равно её истинному значению.
Грубые погрешности (промахи) – погрешности наблюдений, значительно отличающиеся от погрешностей других наблюдений. Обычно носят чисто субъективный характер.
Обработка результатов прямых измерений
Измерение диаметра D цилиндра
Приборы: микрометр с ценой деления 0.01 мм, предел допускаемой погрешности (ПДП), указанный в паспорте микрометра, ![]()
| N | 1 | 2 | 3 | 4 | 5 | Вычисляемые величины |
| D , мм | 2.29 | 2.27 | 2.31 | 2.29 | 2.26 | |
DD ×102 , мм |
+ 0.6 |
– 1.4 |
+ 2.6 |
+ 0.6 |
– 2.4 |
|
(DD )2 ×104 , мм2 |
0.36 |
1.96 |
6.76 |
0.36 |
5.76 |
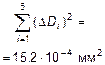 |
1. Исключение систематических погрешностей (если это возможно)
1.1. Считаем, что в данном случае систематическая погрешность отсутствует.
2. Вычисление результата измерения
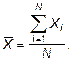
2.1.
![]()
3. ![]() Þ равенство нулю или близость к нулю суммы отклонений
подтверждает правильность расчёта отклонений
DXi
.
Þ равенство нулю или близость к нулю суммы отклонений
подтверждает правильность расчёта отклонений
DXi
.
3.1. ![]() Þ следовательно, расчёт отклонений произведён правильно!
Þ следовательно, расчёт отклонений произведён правильно!
4. СКО результата наблюдения
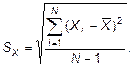
4.1. 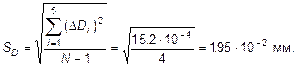
5. Определение промахов
![]()
P = 95% N = 5 VPN = 1.9 (1.67)
N = 10 VPN = 2.3(2.18)
V > VPN ® промах!
Этот результат исключают и снова выполняют п.п. 2,3,4,5, но при N1 = N – 1 .
5.1. ![]() следовательно, считать результат D
3
промахом основания нет!
следовательно, считать результат D
3
промахом основания нет!
6. СКО результата измерения
![]()
6.1. ![]()
7. Доверительная граница случайной погрешности
![]()
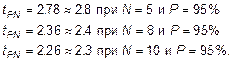
7.1. ![]()
8. Определение суммарной доверительной погрешности результата измерения
![]()
8.1. ![]()
9. Запись окончательного результата
![]()
9.1. Диаметр цилиндра равен
D = (2.28 ± 0.03) мм
при числе наблюдений N = 5 и доверительной вероятности Р = 95%.
Обработка результатов косвенных измерений
Метод переноса погрешностей (метод средних)
Определение ускорения свободного падения
с помощью математического маятника
Приборы: линейка с ценой деления 1 мм; цифровой электронный секундомер с ценой деления 10–2 с.
Расчётная формула
![]()
где L – длина маятника, измеряемая линейкой; Т – период колебаний маятника.
Период колебаний математического маятника определяется как
![]()
где t – время полных п колебаний маятника, измеряемое электронным секундомером. Принимаем п = 10.
| N | 1 | 2 | 3 | 4 | 5 |
| Li , м | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| ti , с | 14.18 | 13.94 | 15.20 | 13.38 | 13.92 |
| Dti , с | 0.056 | – 0.184 | 1.076 | – 0.744 | – 0.204 |
1. Результат измерения длины математического маятника
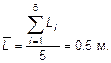
Поскольку случайных погрешностей и промахов, очевидно, нет, то
![]()
2.1. Время 10 полных колебаний маятника
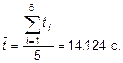
2.2. СКО наблюдения
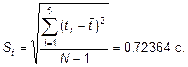
2.3. Проверка на промахи
![]() .
.
Следовательно, промахов нет!
2.4. СКО результата измерения времени
![]()
2.5. Доверительная граница случайной погрешности измерения времени
![]()
2.6. Полная погрешность результата измерения времени
![]()
2.7. Результат измерения времени
![]()
3. Следовательно, ускорение свободного падения (его среднее значение) равно
![]()
4. Полная доверительная граница результата определения ускорения свободного падения
4.1.![]()
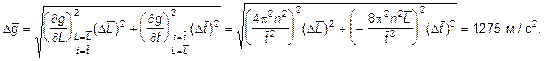
4.2. 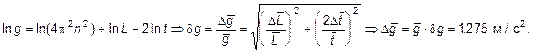
5. Окончательный результат
![]()
Выборочный метод, или метод выборки
Определение ускорения свободного падения
с помощью математического маятника
Приборы: масштабная линейка с ценой деления 1 мм, электронный частотомер с ценой деления 10–2 с.
Расчётная формула:
![]()
где L – длина математического маятника, измеряемая линейкой, Т – период колебаний маятника, измеряемый электронным секундомером. Поскольку измеряется время t полных п = 10 колебаний маятника, то уточнённая расчётная формула имеет вид
![]()
| N | 1 | 2 | 3 | 4 | 5 |
| Li , м | 0.5 | 0.6 | 0.7 | 0.8 | 1.0 |
| ti , c | 14.18 | 15.54 | 16.78 | 17.95 | 20.07 |
| gi , м/с2 | 9.817 | 9.809 | 9.815 | 9.802 | 9.801 |
| Dgi , м/с2 | 0.0082 | 0.0002 | 0.0062 | – 0.0068 | – 0.0078 |
| 1.729 | 1.533 | 1.390 | 1.278 | 1.115 |
1. Находим для каждого наблюдения значение gi и заносим в таблицу.
2. Вычисляем результат измерения
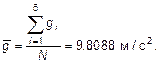
3. СКО наблюдения
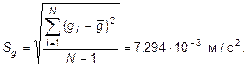
4. Проверка на промахи
![]()
Следовательно, промахов нет!
5. СКО измерения
![]()
6. Доверительная граница случайной погрешности
![]()
7. Граница приборной погрешности
7.1.

7.2. 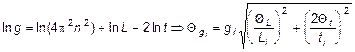 ; по этой формуле находим 5 (!) значений приборной погрешности
; по этой формуле находим 5 (!) значений приборной погрешности ![]() и заносим их в таблицу.
и заносим их в таблицу.
7.3. Среднее значение приборной погрешности
![]()
8. Полная погрешность результата измерения ускорения свободного падения
![]()
9. Окончательный результат
![]() м/с2
.
м/с2
.