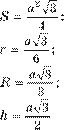| Скачать .pdf |
Реферат: Геометрия 10 класс Бевз профиль

ШАНОВНІ СТАРШОКЛАСНИКИ!
Геометрія – одна з найдавніших, найшляхетніших, корисних і цікавих наук. У ній – згусток значної частини загальнолюдської культури, надбаної людством за кілька тисячоліть. А ще вона є незамінним інструментарієм для науковців і виробничників, засобом для розвитку логічного мислення, просторової уяви, раціоналізаторських здібностей та інших корисних якостей волі і характеру молоді.
 Ось що писав про геометрію відомий архітектор XX ст. Ле Корбюзьє: «Тільки дотримуючись законів геометрії, архітектори давнини могли створити свої шедеври. Невипадково кажуть, що піраміда Хеопса – німий трактат з геометрії, а грецька архітектура – зовнішнє відображення геометрії Евкліда. Минули століття, але роль геометрії не змінилась. Як і раніше, вона залишається граматикою архітектора». І не тільки архітектора чи інженера-конструктора. Ця наука є своєрідною граматикою кожного фахівця, який використовує геометричні форми.
Ось що писав про геометрію відомий архітектор XX ст. Ле Корбюзьє: «Тільки дотримуючись законів геометрії, архітектори давнини могли створити свої шедеври. Невипадково кажуть, що піраміда Хеопса – німий трактат з геометрії, а грецька архітектура – зовнішнє відображення геометрії Евкліда. Минули століття, але роль геометрії не змінилась. Як і раніше, вона залишається граматикою архітектора». І не тільки архітектора чи інженера-конструктора. Ця наука є своєрідною граматикою кожного фахівця, який використовує геометричні форми.
Геометрія складається з двох частин: планіметрії і стереометрії. У попередніх класах ви вивчали в основному планіметрію, тепер переходите до вивчення стереометрії (від грец. – просторовий), в якій розглядаються властивості геометричних фігур у просторі.
Стереометрія – геометрія тривимірного простору. За змістом вона багатша від планіметрії і цікавіша, оскільки вивчає властивості як плоских геометричних фігур, так і неплоских.
Перший розділ, за програмою, – матеріал для повторення, систематизації та узагальнення найважливіших відомостей з планіметрії.
Новий навчальний матеріал викладено в трьох розді лах і додатках. Ко жен з розділів містить теоретичний матеріал і задачі. Читаючи теорію, основну увагу слід звертати на слова, надруковані курсивом і жирним шрифтом. Курсивом виділено геометричні терміни, назви понять. Потрібно вміти пояснювати їх зміст, наводити відповідні приклади. Жирним шрифтом на друковано важливі геометричні твердження, зокрема теореми.
У кожному параграфі підручника є рубрика допитливих». Вона містить додаткові відомості для тих, хто
хоче знати більше. У рубриці ![]() «Виконаємо разом» наводяться задачі з розв’язаннями. Радимо переглянути їх, перш ніж виконувати домашнє завдання.
«Виконаємо разом» наводяться задачі з розв’язаннями. Радимо переглянути їх, перш ніж виконувати домашнє завдання.
Знати геометрію – це насамперед уміти користуватися нею. Вчитися користуватися геометричними знаннями найкраще під час розв’язування геометричних задач. Завдання, рекомендовані для домашньої роботи, виділено кольором. Задачі і вправи в підручнику поділено на: ![]() «Виконайте усно», рівень А,
«Виконайте усно», рівень А,
рівень Б і ![]() «Вправи для повторення». У кожному розділі є задачі за готовими малюнками. Умови таких задач подано малюнками і короткими записами.
«Вправи для повторення». У кожному розділі є задачі за готовими малюнками. Умови таких задач подано малюнками і короткими записами.
Для узагальнення і систематизації вивченого матеріалу подано «Головне в розділі». Перевірити, наскільки ви зас воїли новий матеріал, та підготуватися до зовнішнього незалежного оцінювання ви зможете, розв’язуючи задачі та виконуючи
завдання з рубрик ![]() «Тестові завдання» і
«Тестові завдання» і ![]() «Типові задачі для контрольної роботи».
«Типові задачі для контрольної роботи».
![]() Програмну тему «Ортоцентричний тетраедр» дещо розширено і вміщено в додатках «Елементи геометрії тетраедра». Там міститься ще кілька тем, в яких поглиблено розглядаються деякі найважливіші властивості найпростішого многогранника – тетраедра. Ці теми адресуємо для самостійного опрацювання тим учням, які мають бажання займатися посильною для початківців науково-дослідною роботою. А задачі, що є в «Додатках», можна пропонувати всім учням.
Програмну тему «Ортоцентричний тетраедр» дещо розширено і вміщено в додатках «Елементи геометрії тетраедра». Там міститься ще кілька тем, в яких поглиблено розглядаються деякі найважливіші властивості найпростішого многогранника – тетраедра. Ці теми адресуємо для самостійного опрацювання тим учням, які мають бажання займатися посильною для початківців науково-дослідною роботою. А задачі, що є в «Додатках», можна пропонувати всім учням.
Іноді вважають, що найважливіше в геометрії – доведення теорем. Звичайно, учитися доводити теореми – справа корисна. Але не меншу роль у цій науці відіграють поняття, їх означення і класифікації; геометричні фігури, їх побудова і перетворення; геометричні величини, їх вимірювання та обчислення. Один з відомих геометрів XX ст. Д. Гільберт писав: «У величезному саду геометрії кожний може підібрати собі букет за смаком ».
Запрошуємо вас у цей багатий і дивний світ Геометрії.
Автори

§ 1 ОПОРНІ ФАКТИ ПЛАНІМЕТРІЇ
Пригадаємо найважливіші відомості з планіметрії, які часто використовуються в стереометрії.
Аксіоми планіметрії . Основне в геометрії – її поняття і твердження. Для більшості понять формулюються означення, але існують поняття неозначувані. Це – точка , пряма , площина та деякі інші.
 Переважну більшість геометричних тверджень доводять, тобто показують, що вони як логічні наслідки випливають з інших істинних тверджень. А як бути, коли на початку курсу ще немає «інших тверджень»? У цих випадках кілька тверджень приймають за істинні без доведень. Їх називають аксіомами
. А доводжувані твердження – теоремами
.
Переважну більшість геометричних тверджень доводять, тобто показують, що вони як логічні наслідки випливають з інших істинних тверджень. А як бути, коли на початку курсу ще немає «інших тверджень»? У цих випадках кілька тверджень приймають за істинні без доведень. Їх називають аксіомами
. А доводжувані твердження – теоремами
.
Для планіметрії, як і для інших наук чи теорій, можна обирати різні системи аксіом. Одна з них може бути такою.
1. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що їй не належать.
2. Через будь-які дві різні точки можна провести пряму і тільки одну.
3. Із трьох точок прямої одна і тільки одна лежить між двома іншими.
4. Кожний відрізок має певну довжину.
5. Кожний кут має певну міру.
6. Пряма розбиває площину на дві півплощини.
7. На будь-якій прямій від заданої точки у заданому напрямі можна відкласти відрізок даної довжини і тільки один.
8. Від будь-якого променя у даній півплощині можна відкласти даний кут з вершиною у початку променя і тільки один.
9. Який би не був трикутник, існує рівний йому трикутник у заданому розміщенні відносно заданої прямої.
10. Через точку, що не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній прямій (ак сіо ма Евкліда) .
Розділи про геометричні величини, геометричні перетворення і побудови потребують додаткових аксіом.
Паралельні і перпендикулярні прямі . Дві прямі однієї площини називаються паралельними, якщо вони не перетинаються. Два відрізки або промені називають паралельними, якщо вони належать паралельним прямим.
 Мал. 3
Мал. 3
Геометричним місцем точок площини, рівновіддалених від кінців відрізка, є серединний перпендикуляр до цього відрізка (мал. 5).
Якщо АО ВО і СО АВ , то АС ВС .
Геометричне місце точок кута, рівновіддалених від його сторін, – бісектриса цього кута (мал. 6).
Трикутники. Трикутник – замкнена ламана із трьох ланок. Частина площини, обмежена такою ламаною, також називається трикутником. Кожний трикутник має три сторони, три вершини і три кути. Суму сторін трикутника називають його периметром. Якщо сторони трикутника a , b , c , а
протилежні їм кути , , , то:
|b – c | < a < b + c ; + + 180.
Ознаки рівності трикутників . Два трикутники рівні, якщо:
1) дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого
2) сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні і прилеглим до неї кутам другого
3) три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника.
Відрізок, який сполучає середини двох сторін трикутника, – його середня лінія. Середня лінія трикутника паралельна його третій стороні і дорівнює її половині.
Трикутники, в яких усі відповідні кути рівні, а відповідні сторони пропорційні, називаються подібними .
 Основна теорема про подібність трикутників
. Січна пряма, паралельна стороні трикутника, відтинає від нього трикутник, подібний даному.
Основна теорема про подібність трикутників
. Січна пряма, паралельна стороні трикутника, відтинає від нього трикутник, подібний даному.
Ознаки подібності трикутників . Два трикутники подібні, якщо:
1) два кути одного трикутника відповідно дорівнюють двом кутам другого; або
2) дві сторони одного трикутника пропорційні двом сторонам другого, а кути між ними рівні; або
3) три сторони одного трикутника пропорційні трьом сто-
 c
2
a
2
+ b
2
– теорема Піфагора
; – теорема синусів
.
c
2
a
2
+ b
2
– теорема Піфагора
; – теорема синусів
.
ж тільки одне. Центром кола, вписаного в трикутник, є точка перетину його бісектрис.
Кожний трикутник АВС має медіани, бісектриси, висоти, півпериметр, радіус вписаного і описаного кіл, які відповідно позначають: ma , la , ha , р , r , R . Відомо, що:
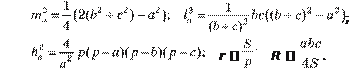
Площа трикутника . Кожний трикутник (як частина площини, обмежена замкненою ламаною) має площу. Формули для визначення площі трикутника:
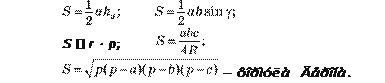
![]() Для прямокутних і рівносторонніх трикутників формули простіші:
Для прямокутних і рівносторонніх трикутників формули простіші:
| Прямокутний трикутник |
Рівносторонній трикутник |
|
|
|
Чотирикутники. Чотирикутник – проста замкнена ламана із чотирьох ланок. Частина площини, обмежена такою ламаною, також називається чотирикутником. Сума всіх кутів кожного чотирикутника дорівнює 360. Кожна сторона чотирикутника менша від суми трьох інших його сторін.
Чотирикутник, кожна сторона якого паралельна протилежній стороні, – паралелограм.
Ознаки паралелограма. Чотирикутник є паралелограмом, якщо:
1) кожна його сторона дорівнює протилежній стороні; 2) дві його протилежні сторони паралельні й рівні;
3) його діагоналі точкою пе ретину діляться навпіл.
Мал. 10
Властивості паралелограма:
– кожна сторона паралелограма паралельна протилежній
– кожний кут паралелограма дорівнює протилежному куту;
– кожна діагональ паралелограма точкою перетину ділиться
– сума квадратів діагоналей паралелограма дорівнює сумі
Окремі види паралелограмів – прямо-
– діагоналі прямокутника (квадрата)
– діагоналі ромба (квадрата) перпендику-
Чотирикутник, у якого тільки дві сто-
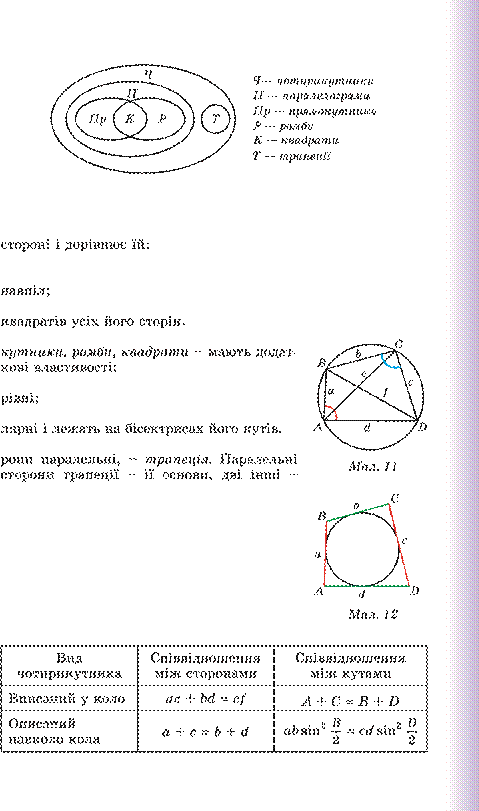 бічні сторони. Окремі види трапецій – рівнобічні і прямокутні трапеції. Відрізок, що сполучає середини бічних сторін трапеції , – її середня лінія.
Середня лінія трапе ції паралельна її основам і дорівнює їх півсумі.
бічні сторони. Окремі види трапецій – рівнобічні і прямокутні трапеції. Відрізок, що сполучає середини бічних сторін трапеції , – її середня лінія.
Середня лінія трапе ції паралельна її основам і дорівнює їх півсумі.
Співвідношення між окремими видами чотирикутників показано на малюнку 10.
Вписані й описані чотирикутники (мал.
11 і 12)
Площі чотирикутників . Площа прямокутника дорівнює добутку двох його сусідніх сторін: S ab.
S aha , або S ab sin ,
де а, b – його сторони, – кут між ними, ha – висота, опущена Якщо діагоналі чотирикутника дорівнюють d 1 і d 2 , а кут
.
Площа трапеції дорівнює добутку півсуми її основ на ви -
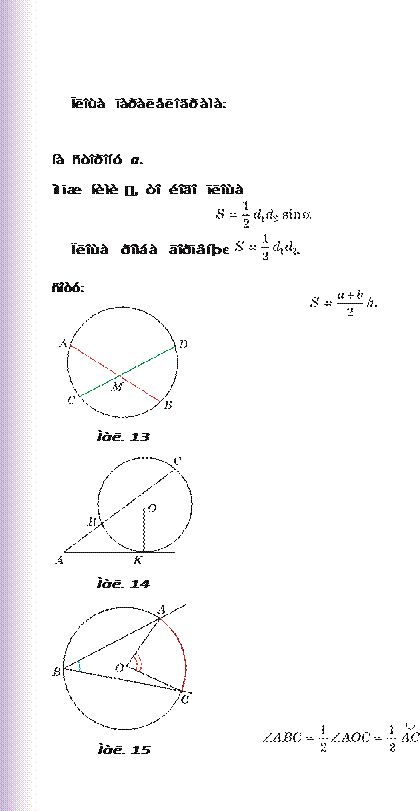 Коло. Кути та відрізки, пов’язані з колом.
Коло – фігура, що складається з усіх точок площини, рівновіддалених від даної точки – центра кола
. Частина площини, обмежена колом, – круг. Радіус –
відрізок, що сполучає будьяку точку кола з його центром. Відрізок, що сполучає дві довільні точки кола, називають хордою.
Хорда, що проходить через центр кола, – діаметр.
Коло. Кути та відрізки, пов’язані з колом.
Коло – фігура, що складається з усіх точок площини, рівновіддалених від даної точки – центра кола
. Частина площини, обмежена колом, – круг. Радіус –
відрізок, що сполучає будьяку точку кола з його центром. Відрізок, що сполучає дві довільні точки кола, називають хордою.
Хорда, що проходить через центр кола, – діаметр.
Пряма, яка має з колом тільки одну спільну точку і лежить у площині кола, називається дотичною до кола.
Мають місце такі властивості:
• діаметр кола, проведений через середину хорди, відмінної від діаметра, перпендикулярний до неї;
• дотична до кола перпендикулярна до радіуса, проведеного в точку дотику;
• відрізки дотичних, проведених до кола з однієї точки, рівні;
• AM BM CM DM (мал. 13);
• AK 2 AB AC (мал. 14);
• вписаний кут вимірюється половиною дуги, на яку він спирається (мал. 15):
;
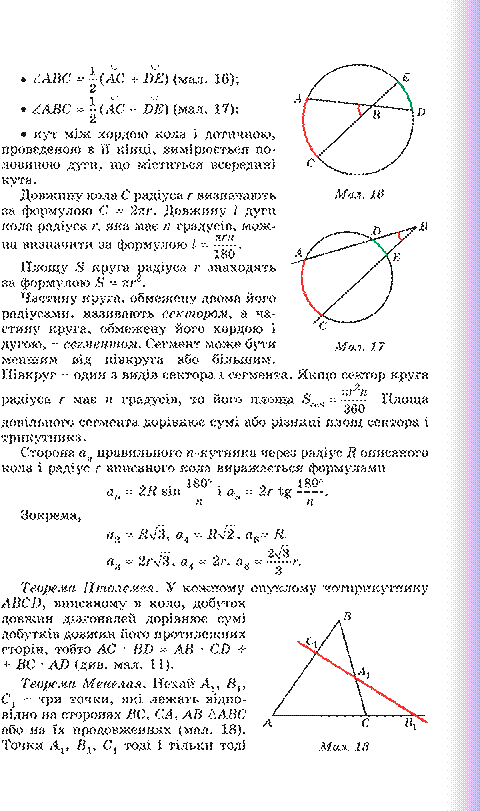 |
лежать на одній прямій, коли, враховуючи напрями від різків,
![]()
Теорема Чеви . Нехай A 1 , B 1 , C 1 – три точки, які лежать відповідно на сторонах BC , CA , AB ABC або на їх продовженнях (мал. 19). Для того щоб прямі AA 1 , BB 1 і CC 1 перетиналися в одній точці або були всі паралельні, необхідно і достатньо, щоб виконувалась умова:
![]()
Останню рівність називають умовою Чеви .
Пряма Ейлера . Ортоцентр H трикутника, його центроїд M і центр O описаного кола лежать на одній прямій (мал. 20), причому OM : MH 1 : 2.
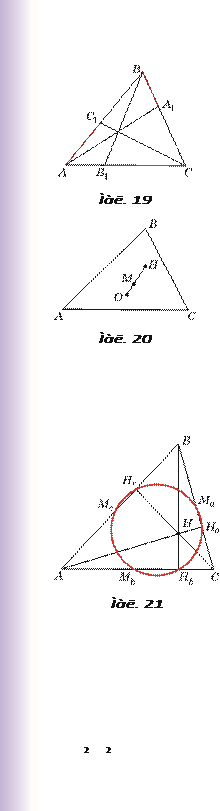 Коло Ейлера
(коло дев’яти точок). Основи висот трикутника, середини його сторін і середини відрізків, які сполучають ортоцентр трикутника з його вершинами, лежать на
Коло Ейлера
(коло дев’яти точок). Основи висот трикутника, середини його сторін і середини відрізків, які сполучають ортоцентр трикутника з його вершинами, лежать на
одному колі (мал. 21). Центр цього кола збігається із серединою відрізка, який сполучає ортоцентр трикутника і центр описаного кола. Його радіус дорівнює половині радіуса описаного кола.
Пряма Сімсона . Основи перпендикулярів, опущених на сторони трикутника з точки описаного кола, лежать на одній прямій.
Коло Аполлонія . Геометричним місцем точок, відношення відстаней від яких до двох даних точок стале, є коло.
Координати на площині . Площ ину, на якій задано си стему координат, називають координатною площиною. Кожній точці координатної площини відповідає єдина пара дійсних чисел (координати цієї точки), а кожній парі дійсних чисел – єдина точка координатної площини.
Кожна координата середини відрізка дорівнює півсумі відповідних координат його кінців. Тобто якщо кінці відрізка А (х 1 ; у 1 ) і В (х ; у ), то серединою даного відрізка є точка з координатами
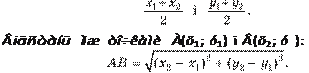 2
2
Квадрат довжини відрізка дорівнює сумі квадратів його проекцій на дві взаємно перпендикулярні прямі.
Рівнянням фігури на координатній площині називають рівняння з двома змінними, яке задовольняють координати кожної точки даної фігури і тільки вони.
Рівняння кола радіуса r із центром у точці А (а ; b ) має вигляд (х – а )2 + (у – b )2 r 2 .
Якщо центр кола радіуса r лежить у початку координат, то
його рівняння х 2 + у 2 r 2 .
Кожній прямій координатної площини відповідає лінійне рівняння з двома змінними ax + by + с 0. Таке рівняння називають загальним рівнянням прямої.
Рівність y kx + b – рівняння прямої з кутовим коефі ціє нтом. Тут k tg, де – кут, який утворює пряма з додатним напрямом осі ОХ .
– рівняння прямої, що проходить через дві
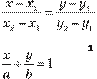
![]() дані точки A
(x
; y
1
) і В
(х
2
; у
2
).
дані точки A
(x
; y
1
) і В
(х
2
; у
2
).
– рівняння прямої у відрізках на осях (числа а і b
показують, які відрізки пряма l відтинає на осях координат). Якщо прямі l 1 і l 2 задані рівняннями y 1 k 1 x + b 1 і y 2 k 2 x + b 2 ,
то:
1) l 1 l 2 тоді і тільки тоді, коли k 1 k 2 ; 2) l 1 l 2 тоді і тільки тоді, коли k 1 · k 2 –1.
Векторні величини – ті, які визначаються не тільки числовими значеннями, а й напрямами. Значення векторних величин – вектори . Геометрично вектори (ненульові) зображаються напрямленими відрізками. Напрямлений відрізок має початок і кінець. Відстань між ними – модуль (довжина) вектора.
Два вектори називають колінеарними, якщо відповідні їм напрямлені відрізки розташовані на одній прямій або на паралельних прямих. Колінеарні вектори бувають співнапрямленими або протилежно напрямленими. Два вектори рівні , якщо вони співнапрямлені і мають рівні модулі. Два вектори називають протилежними , якщо вони мають рівні модулі і протилежно напрямлені.
Координатами вектора з початком A (x 1 ; у 1 ) і кінцем В (x 2 ; y 2 ) називають числа x x 2 – x 1 і y y 2 – y 1 .
Записують такий вектор у вигляді:
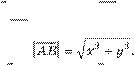 AB
(x
; y
), або a
(x
; y
), або AB
(x
2
– x
1
; y
2
– y
1
).
AB
(x
; y
), або a
(x
; y
), або AB
(x
2
– x
1
; y
2
– y
1
).
![]()
Модуль вектора AB (x ; y ) позначають символом |AB |:
Су мою векторів a (x 1 ; y 1 ) і b (x 2 ; y 2 ) називають вектор a + b (x 1 + x 2 ; y 1 + y 2 ). Для додавання векторів виконуються переставний і сполучний закони.
Геометрично додавати вектори можна за правилом трикутника або паралелограма (мал. 22 і 23). Завжди правильні векторні рівності:
AB + BC AС , AB + BC + CD AD .
 Рі
зницею векторів a
(x
1
; y
1
) і b
(x
2
; y
2
) називають вектор a
– b
(x
1
– x
2
; y
1
– y
2
).
Рі
зницею векторів a
(x
1
; y
1
) і b
(x
2
; y
2
) називають вектор a
– b
(x
1
– x
2
; y
1
– y
2
).
![]()
Різниця векторів AB і KP дорівнює AB + PK . Щоб відняти від одного вектора другий, треба до першого додати вектор, протилежний другому.
![]()
Які не були б вектори AB і AC , завжди AB – AC CB .
 Добутком вектора a
(x
; y
) на число n
називають вектор na
(nx
; ny
). Завжди правильні рівності:
Добутком вектора a
(x
; y
) на число n
називають вектор na
(nx
; ny
). Завжди правильні рівності:
(n + m ) a na + ma і n (a + b ) na + nb .
Скалярним добутком двох ненульових векторів називають добуток модулів цих векторів на косинус кута між ними:
![]()
a b |a | |b | cos .
Якщо хоч один з векторів нульовий, то їх скалярний
добуток дорівнює нулю.

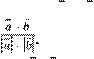 Кут між ненульовими векторами a
і b
можна знайти, кори стуючись формулою cos Якщо a
(x
1
; y
1
) і b
(x
2
; y
2
), то a
b
x
1
x
2
+ у
1
у
2
.
Кут між ненульовими векторами a
і b
можна знайти, кори стуючись формулою cos Якщо a
(x
1
; y
1
) і b
(x
2
; y
2
), то a
b
x
1
x
2
+ у
1
у
2
.
a kb або – умова колінеарності ненульових векторів a і b (k 0); a b 0 або x 1 x 2 + y 1 y 2 0 – умова їх пер пен ди ку ляр ності.
a b

a + b b
Мал. 22 Мал. 23
|
2. 3. 4. 5. 6. 7. 8. 9. 10. 12. 13. 14. 15. 16. 17. 18. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 31. |
ЗAПИТAННЯ І ЗAВДAННЯ ДЛЯ САМОКОНТРОЛЮ
Що таке геометрія? Що таке планіметрія?
Наведіть приклади плоских і неплоских фігур.
Що означають записи А а , В а ?
Як слід розуміти вислів «точка В лежить між А і С »?
Що таке промінь? Як позначають промені?
Що таке відрізок? Що таке кінці відрізка?
Що таке відстань між двома точками?
Яка фігура називається кутом? Як позначають кути? Який кут називають гострим? Прямим? Тупим? Розгорнутим?
Які кути називають суміжними? Чому дорівнює їх сума? Які кути називають вертикальними? Сформулюйте теорему про вертикальні кути. Які прямі називають перпендикулярними?
Сформулюйте означення паралельних прямих.
Сформулюйте ознаку паралельності прямих.
![]() Сформулюйте аксіому Евкліда про паралельність прямих.
Сформулюйте аксіому Евкліда про паралельність прямих.
Що таке трикутник? Назвіть елементи трикутника.
Якими бувають трикутники?
Що таке бісектриса, медіана, висота трикутника?
Cформулюйте теорему про суму кутів трикутника.
Сформулюйте ознаки рівності трикут ників. Який трикутник називають рівнобедреним?
Сформулюйте кілька властивостей рівнобедреного трикутника. Як називають сторони прямокутного трикутника?
Сформулюйте ознаки рівності прямокутних трикутників.
Що таке перпендикуляр, похила, проекція похилої?
Що таке відстань від точки до прямої?
Що таке коло? Центр? Радіус? Діаметр? Хорда?
Що таке круг? Чим відрізняється круг від кола?
Сформулюйте означення і властивість дотичної до кола.
Що таке центральний кут? Вписаний кут?
| 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. 61. 62. 63. |
Сформулюйте теорему про вписані кути.
Як побудувати трикутник за трьома даними сторонами? Як побудувати кут, що дорівнює даному? Як побудувати бісектрису даного кута? Як поділити даний відрізок навпіл?
Як через дану точку провести пряму, перпендику ляр ну до даної прямої? А паралельну даній прямій?
Що таке геометричне місце точок? Наведіть прик лади.
Що таке серединний перпендикуляр даного від різка? Як навколо даного трикутника описати коло? Як у даний трикутник вписати коло?
Що таке чотирикутник?
Сформулюйте означення паралелограма.
Які властивості має паралелограм? Сформулюйте ознаки паралелограма.
Що таке прямокутник? Які властивості має прямокут ник?
![]() Що таке ромб? Квадрат? Назвіть їх властивості.
Що таке ромб? Квадрат? Назвіть їх властивості.
Сформулюйте теорему Фалеса.
Сформулюйте теорему про середню лінію трикутника. Що таке трапеція? Рівнобічна трапеція? Прямокутна трапеція?
Сформулюйте теорему про середню лінію трапеції. Які трикутники називають подібними?
Сформулюйте ознаки подібності трикут ників.
Сформулюйте теорему Піфагора.
Як знайти координати середини відрізка?
Як знайти відстань між точками з даними координатами?
Що таке рівняння фігури?
Яке рівняння має коло? Пряма? Наведіть приклади векторних величин. Як зображають вектори?
Що таке координати вектора?
Що таке довжина вектора?
Які вектори називають рівними? Колінеарними?
Протилежними?
| 64. 65. 66. 67. 68. 69. 70. 71. 72. 73. 74. 75. 76. 77. 78. 79. 80. |
Що таке сума двох векторів?
Сформулюйте правило трикутника для додавання векторів.
Сформулюйте правило паралелограма для додаван ня векторів.
Що таке різниця векторів? Як її знаходять?
Сформулюйте правило множення вектора на число.
Сформулюйте властивості множення вектора на число.
Що таке синус, косинус, тангенс кута?
Сформулюйте теорему косинусів.
Сформулюйте теорему синусів.
Що таке многокутник?
Чому дорівнює сума кутів опуклого n - кутника?
Сформулюйте означення правильного многокутника.
За якою формулою знаходять довжину кола?
Що таке площа многокутника?
За якими формулами обчислюють площі прямокутника, паралелограма, трикутника, трапеції?
Сформулюйте теорему про відношення площ подібних многокутників.
За якою формулою знаходять площу круга?
ПЕРЕВІРТЕ СЕБЕ
Тематичні завдання в тестовій формі
Прямі і кути
1. Установіть, на скільки частин можуть розбити площи ну дві її прямі.
а) На 2 або на 3; б) на 2 або на 4;
в) на 3 або на 4; г) на 3 або на 5.
2. Якщо один із суміжних кутів на 80 більший від другого, то другий кут дорівнює:
а) 80; б) 140; в) 50; г) 120.
3. Відомо, що a c i b c . Укажіть правильне відношення.
а) a b ; б) a b ; в) a || b ; г) a b .
4.
 Кут між однією з двох паралельних прямих і їх січною дорівнює 60. Під яким кутом бісектриса цього кута перетинає другу пряму?
Кут між однією з двох паралельних прямих і їх січною дорівнює 60. Під яким кутом бісектриса цього кута перетинає другу пряму?
а) 60; б) 40; в) 30; г) 120.
5. Скільки прямих можна провести через дві різні точки?
а) Одну; б) дві; в) три; г) жодної.
6. Вписаний кут, що спирається на діаметр, дорівнює:
а) 180; б) 80; в) 45; г) 90.
7. Яким знаком не позначають взаємне розташування двох прямих?
а) a b ; б) a b ; в) a || b ; г) a b .
8. Прямі а і b не паралельні прямій с . Чи випливає з цього, що прямі а і b не паралельні?
а) Так; б) ні; в) так, якщо a с ; г) ні, якщо b с .
9. Скільки пар вертикальних кутів утворюють три прямі, що перетинаються в одній точці?
а) 3; б) 6; в) 9; г) 12.
10.
 На одній стороні кута відкладено три відрізки АВ
2, ВС
3 і СD
5. Через точки А
, В
, С
і D
проведено паралельні прямі АА
1
, ВВ
1
, СС
1
і DD
1
до перетину з іншою стороною кута. Знайдіть В
1
С
1
, якщо А
1
D
1
20.
На одній стороні кута відкладено три відрізки АВ
2, ВС
3 і СD
5. Через точки А
, В
, С
і D
проведено паралельні прямі АА
1
, ВВ
1
, СС
1
і DD
1
до перетину з іншою стороною кута. Знайдіть В
1
С
1
, якщо А
1
D
1
20.
а) 9 ; б) 6; в) 4; г) 10.
Трикутники
1. Якщо кути трикутника пропорційні числам 2, 3 і 4, то його найменший кут дорівнює:
а) 80; б) 40; в) 30; г) 20.
2. Найменший зовнішній кут прямокутного трикутника дорівнює:
а) 180; б) 90; в) 135; г) 125.
3. Площа рівностороннього трикутника зі стороною 2 дм дорівнює:
а) 4 дм2
; б) 2![]() дм2
; в)
дм2
; в) ![]() дм2
; г) 0,5
дм2
; г) 0,5 ![]() дм2
.
дм2
.
4. Знайдіть радіус кола, описаного навколо трикутника АВС , якщо АС 3 см, B 30.
а) 3 см; б) 6 см; в) ![]() см; г) 12 см.
см; г) 12 см.
5. Менша медіана прямокутного трикутника з катетами 5 см і 12 см дорівнює:
а) 2,5 см; б) 6,5 см; в) 6 см; г) 5 см.
6. У трикутнику провели три середні лінії. Скільки пар подібних трикутників утворилося?
а) 4 ; б) 6; в) 10; г) 12.
7. За якою формулою обчислюють радіус кола, вписаного в трикутник?
а) б) ![]() в)
в) ![]() г)
г) ![]()
8.
![]() Гіпотенуза рівнобедреного прямокутного трикутника дорівнює , а бісек три са, опущена на неї:
Гіпотенуза рівнобедреного прямокутного трикутника дорівнює , а бісек три са, опущена на неї:
а) ; б) ![]() ; в)
; в) ![]() ; г) .
; г) .
9.
![]() Знайдіть площу трикутника, дві сторони якого дорівнюють 6 см і 14 см, а кут між ними 30.
Знайдіть площу трикутника, дві сторони якого дорівнюють 6 см і 14 см, а кут між ними 30.
а) 42 см2
; б) 21![]() см2
; в) 21 см2
; г) 21 см2
.
см2
; в) 21 см2
; г) 21 см2
.
10. Площі двох подібних трикутників відносяться як 4 : 9. Як відносяться їхні сторони?
а) 16 : 81; б) 2 : 4,5; в) 1 : 2,5; г) 2 : 3.
Чотирикутники
1. Кількість осей симетрії квадрата дорівнює:
а) 2 ; б) 3; в) 4; г) 5.
2. Основи трапеції дорівнюють 4 см і 10 см, а її середня лінія:
а) 4 с;м б) 7 см; в) 10 см; г) 3,5 см.
3. Периметр паралелограма дорівнює 16 см. Одна його сторона – 5 см, а друга:
а) 5 см; б) 6 см; в) 11 см; г) 3 см.
4. Знайдіть кути ромба, якщо вони пропорційні числам 2 і 7.
а) 30 і 70; б) 20 і 140; в) 40 і 140; г) 80 і 280.
5. Менша сторона прямокутника дорівнює 5 см. Знайдіть довжину діагоналі, якщо вона утворює з більшою стороною кут 30.
а) 10 см; б) 5 см; в) 2,5 см; г) 20 см.
6. Знайдіть площу ромба, якщо його менша діагональ і сторона дорівнюють 4 м.
а) 4![]() м2
; б) 6
м2
; б) 6 ![]() м2
; в) 8
м2
; в) 8 ![]() м2
; г) 2
м2
; г) 2 ![]() м2
.
м2
.
7. Якщо бісектриса кута прямокутника ділить його на частини, площі яких пропорційні числам 1 і 3, то його суміжні сторони відносяться як:
а) 1 : 2; б) 1 : 3; в) 1 : 4; г) 2 : 3.
8.
 Периметр рівнобічної трапеції, описаної навколо кола, дорівнює 20 см. Знайдіть бічну сторону трапеції. а) 5 см; б) 6 см; в) 11 см; г) 3 см.
Периметр рівнобічної трапеції, описаної навколо кола, дорівнює 20 см. Знайдіть бічну сторону трапеції. а) 5 см; б) 6 см; в) 11 см; г) 3 см.
9. Знайдіть найбільший кут прямокутної трапеції, якщо один з її кутів уд вічі більший за інший.
а) 130 або 170; б) 120 або 135;
в) 140 або 145; г) 180 або 128.
10. Один з кутів ромба дорівнює 120, а периметр 24 см. Менша діаго наль ромба дорівнює:
а) 2 см; б) 3 см; в) 4 см; г) 6 см.
Коло і круг
1. Довжина чверті кола радіуса 2м дорівнює:
а) 2 м; б) 16 м; в) 2 м; г) 4 м2 .
2. Площа круга дорівнює 100 см2 . Знайдіть довжину його кола.
а) 100 см; б) 50 см; в) 20 см; г) 2500 см.
3. Кут між двома радіусами кола дорівнює 125. Знайдіть кут між дотичними, проведеними через кінці цих радіусів. а) 125; б) 95; в) 35; г) 55.
4.
Під яким кутом із центра кола, вписаного в рівносторонній трикутник, видно сторону цього трикутника? а) 30; б) 60; в) 90; г) 120.
5. Радіус кола, описаного навколо правильного шестикутника з периметром 24 см, дорівнює:
а) 12 см; б) 3 см; в) 6 см; г) 4 см.
6. Кола радіусів 3 м і 7 м мають внутрішній дотик. Відстань між їхніми центрами:
а) 2 м; б) 10 м; в) 4 м; г) 5 м.
7. Знайдіть площу кільця, утвореного концентричними колами радіусів 3 м і 5 м.
а) 2 м2 ; б) 16 м2 ; в) 2 м2 ; г) 4 м2 .
8. Сторона квадрата, описаного навколо кола завдовжки 16 см, дорівнює:
а) 16 см; б) 8 см; в) 4 см; г) 4![]() см.
см.
9.
 Правильний трикутник ABC
вписаний у коло. Знайдіть довжину кола, якщо довжина дуги ВАС
дорівнює 6 см. а) 12 см; б) 12 см; в) 9 см; г) 4
Правильний трикутник ABC
вписаний у коло. Знайдіть довжину кола, якщо довжина дуги ВАС
дорівнює 6 см. а) 12 см; б) 12 см; в) 9 см; г) 4![]() см.
см.
10. Знайдіть площу сектора круга радіуса 6 см з центральним кутом 60.
а) 6 см2 ; б) 3 см2 ; в) 9 см2 ; г) 2 см2 .
Координати на площині
1. Середина відрізка KР , де K (1; –3), Р (7; 5), має коор динати:
а) (–1; 3); б) (4; 1); в) (2; 1); г) (3; 4).
2. Який знак слід поставити в запису АС * ВС замість зірочки, якщо А (–1; 3), В (5; 6), С (2; 4,5)?
а) >; б) <; в) ; г) .
3. Яка з точок не належить прямій 2х + у 7?
а) (–2; 11); б) (–0,5; 8); в) (2; 5); г) (0,5; 6).
4.
Прямій у
![]() х
+ 5 паралельна пряма:
х
+ 5 паралельна пряма:
а) у 5; б) 3х + у 4; в) 2у – х 2; г) х + [1] у 6.
5. Пряма х + у 5 утворює з додатним напрямом осі ОХ кут:
а) 90; б) 45; в) 135; г) 30.
6. Центр кола х 2 + (у – 2)2 – 8 0 має координати:
а) (0; 4); б) (1; 2); в) (0; 2); г) (2; 4).
7. Точка М , яка лежить на осі ОХ та рівновіддалена від точок А (5; 4) і В (2; 1), має координати:
а) (0; 4); б) (1; 0); в) (0; 2); г) (6; 0).
8. Коло з діаметром АВ , де А (4; 3), В (–4; –3), має рів няння:
а) х 2 + у 2 5; б) х 2 + у 2 9;
в) х 2 + у 2 25; г) х 2 + у 2 3.
9.
 Якщо діаметр кола х
2
+ у
2
25 проходить через точку А
(3; 4), то його рівняння:
Якщо діаметр кола х
2
+ у
2
25 проходить через точку А
(3; 4), то його рівняння:
а) 3х + 4у 25; б) 3у 4х ;
в) у + х 5; г) 4х + 3у 0.
10. Яка з прямих не є дотичною до кола х 2 + (у – 2)2 9?
а) х ;3 б) у 3; в) х –3; г) у –1.
Вектори
1. Якщо А (1; –3) і В (–7; 12), то вектор AB має координати:
а) (6; –15); б) (–8; 15); в) (–8; 9); г) (–6; 9).
2.
 Якщо вектори a
і b
перпендикулярні, то:
Якщо вектори a
і b
перпендикулярні, то:
а) a + b 0; б) a – b 0;
в) a · b 0; г) a : b 0.
4. Знайдіть довжину вектора a (–2; 4).
 а) 2
а) 2![]() ; б) 20; в) 12; г) 2 .
; б) 20; в) 12; г) 2 .
5. Вектор, колінеарний вектору a (–1; 4), має координати:
а) (–2; –8); б) (0,5; 2); в) (3; –3); г) (4; –16).
6. Сумою векторів BC + AB + DA + CD є вектор:
![]()
а) AВ ; б) AC ; в) 0; г) AD .
7. Якщо скалярний добуток двох одиничних векторів дорівнює 0,5, то кут між ними:
а) 30; б) 60; в) 120; г) 45.
![]()
8. При якому значенні т вектори a (–2; 6) і b (9; т ) перпендикулярні?
а) –3; б) 27; в) 3; г) –27.
![]()
9. При якому значенні х вектори m (3; х ) і n (–6; 7) колінеарні?
а) 14; б) 3,5; в) –3,5; г) –14.
10.
![]() Проекції вектора AB
на осі х
і у
дорівнюють відповідно а
і b
, а проекція вектора BA
на вісь у
дорівнює: а) –а
; б) –b
; в) b
; г) а
.
Проекції вектора AB
на осі х
і у
дорівнюють відповідно а
і b
, а проекція вектора BA
на вісь у
дорівнює: а) –а
; б) –b
; в) b
; г) а
.
МЕТОДИ РОЗВ’ЯЗУВАННЯ
§ 2 ПЛАНІМЕТРИЧНИХ ЗАДАЧ
 Планіметричні задачі бувають різних видів, здебільшого – на обчислення, побудову, доведення чи дослідження. У задачах на обчислення
найчастіше вимагається знайти значення геометричної величини: відстань, довжину дуги, міру кута, периметр чи площу фігури.
Планіметричні задачі бувають різних видів, здебільшого – на обчислення, побудову, доведення чи дослідження. У задачах на обчислення
найчастіше вимагається знайти значення геометричної величини: відстань, довжину дуги, міру кута, периметр чи площу фігури.
ЗАДАЧА 1. Знайдіть суму кутів А, В, С, D, Е зірки, зображеної на малюнку 24.
РОЗВ’ЯЗАННЯ. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним. Тому, позначивши на малюнку два кути цифрами 1 і 2 , маємо:
В + D 1 , С + Е 2. Отже,
C
А + В + С + D + Е А +
B D + 1 +2 180.
ВІДПОВІДЬ. Сума кутів кожної
2 1 такої п’ятикутної зірки дорівнює
180.
A E У задачах на побудову вимага-
Мал. 24 ється побудувати фігуру зі вказаними
 |
ЗАДАЧА 3. Доведіть, що сума відстаней від довільної точки Х внутрішньої області правильного трикутника до його сторін стала, тобто не залежить від положення цієї точки.
РОЗВ’ЯЗАННЯ. Нехай АВС – правильний трикутник зі стороною а і
C висотою h , Х – довільна точка у його внутрішній області, а ХK , ХР , ХТ – перпендикуляри до АВ , ВС , АС (мал. 27).
Виразимо двома способами площу S
Відрізки ХА , ХВ , ХС даний трикутник розбивають на три трикутники з основами АВ , ВС , СА і висотами ХK , ХР , ХТ . Їх подвоєні площі дорівнюють а · ХK , а · ХР , а · ХТ , а подвоєна площа всього трикутника а · h . Отже, а · ХK + а · ХР + а · ХТ а · h , звідси ХK + ХР + ХТ h.
Отже, де б не була точка Х (усередині ABC ), сума відстаней від неї до сторін не змінюється і дорівнює h .
У задачах на дослідження пропонується дослідити що-неб удь.
ЗАДАЧА 4. Кожна сторона пара ле ло грама паралельна проти лежній стороні. А чи існує чотирикутник, кожна стор о на якого перпендикулярна до про ти лежної сторони?
 РОЗВ’ЯЗАННЯ.
Перший спосіб
. Спроб уємо накреслити хоча б один з таких чотирикутників. Нехай АВ
і СD
– його прот илежні сторони – перпендикулярні відрізки. Провівши відрізки АD
і ВС
, утворимо чотирикутник АВСD
, у якого АВ
СD
(мал. 28). Дві інші його сторони АD
і ВС
можуть бути не перпен ди кулярні. Але продовживши або вкор о тивши від рі зок АВ
, можна досягти, щоб і вони стали перпендикулярними.
РОЗВ’ЯЗАННЯ.
Перший спосіб
. Спроб уємо накреслити хоча б один з таких чотирикутників. Нехай АВ
і СD
– його прот илежні сторони – перпендикулярні відрізки. Провівши відрізки АD
і ВС
, утворимо чотирикутник АВСD
, у якого АВ
СD
(мал. 28). Дві інші його сторони АD
і ВС
можуть бути не перпен ди кулярні. Але продовживши або вкор о тивши від рі зок АВ
, можна досягти, щоб і вони стали перпендикулярними.
ВІДПОВІДЬ. Чотирикутник, кожна сторона якого перпенди кулярна до про тилежної сторони, існує.
Другий спосіб. Нехай АВС – довільний гострокутний трикутник, а його висоти перетинаються в точці Н (мал. 29).
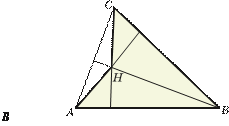
Мал. 29
Зафарбуємо неопуклий чотирикутник АВСН . Кожна його сторона перпендикулярна до протилежної сторони.
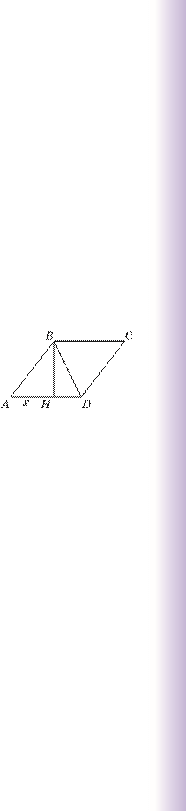 Другий спосіб продуктивніший: він додатково показує, що в такого чотирикутника діагоналі перпендикулярні. А отже, середини сторін чотирикутника АВСН
– вершини прямокутника, а площа чотирикутника АВСН
дорівнює півдобутку діагоналей тощо. Якщо в розв’язанні використовують тільки геометричні відомості, таке розв’язання називають геометричним
. Якщо ж використовують відомості з алгебри чи математичного аналізу, то кажуть про аналітичне розв’язання
. Найчастіше аналітичне розв’язання задачі зводиться до складання за умовою геометричної задачі відповідних рівнянь чи систем рівнянь.
Другий спосіб продуктивніший: він додатково показує, що в такого чотирикутника діагоналі перпендикулярні. А отже, середини сторін чотирикутника АВСН
– вершини прямокутника, а площа чотирикутника АВСН
дорівнює півдобутку діагоналей тощо. Якщо в розв’язанні використовують тільки геометричні відомості, таке розв’язання називають геометричним
. Якщо ж використовують відомості з алгебри чи математичного аналізу, то кажуть про аналітичне розв’язання
. Найчастіше аналітичне розв’язання задачі зводиться до складання за умовою геометричної задачі відповідних рівнянь чи систем рівнянь.
ЗАДАЧА 5. Знайдіть площу ромба, якщо його висота і мен ша діагональ відповідно дорівнюють 12 см і 13 см. РОЗВ’ЯЗАННЯ. Нехай АВСD – ромб
(мал. 30), а ВН і ВD – його висота і ді а- гональ. Тоді ВН 12 см, ВD 13 см, а
НD
![]() (см).
(см).
Нехай АН х. Тоді АВ AD AH +
+ HD x + 5.
З АВН АВ 2 ВН 2 + АН 2 . Можемо Мал. 30 скласти рівняння:
(x + 5)2 122 + х 2 , або х 2 + 10х + 25 144 + х 2 , звідси х 11,9 (см).
Маємо АВ x + 5 11,9 + 5 16,9 (см). Знайдемо тепер площу S ромба АВСD .
S ВН · AD , тобто S 12 · 16,9 202,8 (см2 ).
ВІДПОВІДЬ. S 202,8 см2 .
Ефективними методами розв’язування геометричних задач є координатний і векторний методи.
Координатний метод полягає в тому, що розв’язуючи геометричну задачу, оперують координатами окремих точок, рівняннями прямих або інших ліній. Розв’язуючи задачу координатним методом, розглядувані фігури розміщують на координатній площині. Приписавши окремим точкам фігур координати, а лініям — рівняння, далі обчислюють координати інших точок, виводять рівняння інших ліній. У результаті отримуємо потрібну відповідь.
Раціональність розв’язання задачі цим методом значною мірою залежить від того, як розглядувану фігуру розмістити відносно координатних осей. Найзручніше цим методом користуватися тоді, коли в задачі мова йде про прямі кути або суми квадратів якихось відстаней.
ЗАДАЧА 6. Знайдіть суму квадратів відстаней від довільної точки кола радіуса 5 см до вершин описаного навколо нього квадрата.
РОЗВ’ЯЗАННЯ. Коло радіуса 5 см і описаний навколо нього квадрат розмістимо в системі координат так, щоб її осі були серединними перп ен ди ку лярами для сторін квадрата (мал. 31). Тоді колу відповідатиме рівняння х 2 + + у 2 25, а вершини квадрата мати муть координати А (5; –5), В (5; 5), С (–5; 5),
Якщо М (х ; у ) – довільна точка кола, то МА 2 + МВ 2 + МС 2 + + МD (5 – х ) + (–5 – у )2 + (5 – х )2 + (5 – у )2 + (–5 – х )2 + + (5 – у ) + (–5 – х )2 + (–5 – у )2 2((5 – х )2 + (5 + х )2 + (5 + + у )2 + (5 – у ) ) 200 + 4(х 2 + у 2 ) 300 (см2 ).
2

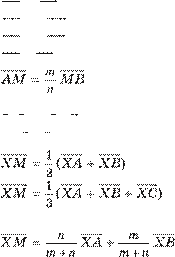 Якщо задачу розв’язують, використовуючи властивості векторів, то це – векторний метод розв’язування задачі. Для ефективного його застосування слід уміти геометричні співвідношення (властивості геометричних фігур) записувати у вигляді векторних рівностей. При цьому часто використовують такі твердження та векторні рівності:
Якщо задачу розв’язують, використовуючи властивості векторів, то це – векторний метод розв’язування задачі. Для ефективного його застосування слід уміти геометричні співвідношення (властивості геометричних фігур) записувати у вигляді векторних рівностей. При цьому часто використовують такі твердження та векторні рівності:
1) OA OB – точки А і В збігаються;
2) AB kCD – прямі АВ і CD паралельні або збігаються;
3) AB kAC – точки А , В , С лежать на одній прямій;
4) AB · CD 0 – прямі АВ і CD перпендикулярні;
5) , а числа m і n додатні – точка М ділить
від різок АВ у відношенні АМ : МВ m : п ;
6) a · b |a | · |b | cos – кут між прямими, на яких лежать вектори a і b , дорівнює ;
– М – середина відрізка АВ ;
– М – точка перетину медіан
– точка М ділить відрізок АВ
Користуючись цими співвідношеннями, можна розв’язувати багато геометричних задач та доводити теореми.
Розв’язування задачі векторним методом складається з кількох кроків:
– подані в задачі співвідношення «перекладають мовою» векторів, тобто записують їх відповідними векторними рівностями;
– отримані векторні рівності перетворюють, використовуючи правила векторної алгебри;
– від мови векторів переходять до мови геометрії.
ЗАДАЧА 7. Точка перетину прямих, яким належать бічні сторони трапеції, та середини її основ лежать на одній прямій. Доведіть.
 РОЗВ’ЯЗАННЯ.
На малюнку 32 зображено трапецію АВСD
. Точки М
і N
– середини її основ, а О
– точка перетину прямих АВ
і СD
. Щоб довести, що точки М
, N
і О
лежать на одній пря мій,
РОЗВ’ЯЗАННЯ.
На малюнку 32 зображено трапецію АВСD
. Точки М
і N
– середини її основ, а О
– точка перетину прямих АВ
і СD
. Щоб довести, що точки М
, N
і О
лежать на одній пря мій,
![]()
покажемо, що вектори OM і ON – ко лінеарні.
Оскільки М – середина ВС , а N – середина AD , то виконуються рівності:
OM (OB + OC ) і ON (OA + OD ).
Оскільки ОВС ОАD , то OA : OB OD : OC k . Звідси
 OA
kOB
, OD
kOC
, ON
(kOB + + kOC
) k
(OB + OC
) kOM.
OA
kOB
, OD
kOC
, ON
(kOB + + kOC
) k
(OB + OC
) kOM.
Маємо ON kOM. Отже, точки М , N і
О лежать на одній прямій. Мал. 32
ЗAДAЧІ І ВПРAВИ
А
1. Через точку на площині проведено 3 прямі. Доведіть, що міри принаймні двох з утворених кутів менші за 61.
2. Установіть вид трикутника, якщо його кути пропорційні числам 1, 2 і 3.
3. Визначте найбільший внутрішній кут трикутника, якщо його зовнішні кути (взяті по одному при вершині) пропорційні числам 2, 3 і 4.
4. Висота і медіана прямокутного трикутника, проведені з вершини прямого кута, ділять кут на три рівні частини.
Знайдіть кут між висотою і бісектрисою, проведеною із цієї вершини.
5. Точка О – спільна середина відрізків AD і BC . Пряма l , що проходить через точку О , перетинає відрізок АВ у точці М , а відрізок CD у точці N . Доведіть:
а) МО NO ; б) AM DN ; в)DNO AMO .
6. У рівнобедреному трикутнику АВС проведено медіани АМ і BN до бічних сторін. Доведіть:
а) АМВ BNA ; б) CAM CBN.
7. У рівнобедреному трикутнику АВС проведено бісектриси АМ і BN до бічних сторін. Доведіть:
а) АМВ BNA ; б) CAM CBN .
8. Побудуйте рівнобедрений трикутник, у якого бічна сторона і висота, проведена до основи, дорівнюють відповідно 8 см і 6 см.
9. Побудуйте прямокутний трикутник, у якого один з катетів дорівнює 3 см, а медіана, проведена до іншого катета, 6 см.
10. Поділіть заданий відрізок на 7 рівних частин.
11. Сума двох сусідніх кутів опуклого чотирикутника дорівнює 100. Знайдіть кут між бісектрисами двох інших його кутів.
12.
![]() Знайдіть усі медіани прямокутного трикутника з катетами 3,2 см і 4,8 см.
Знайдіть усі медіани прямокутного трикутника з катетами 3,2 см і 4,8 см.
13. Бісектриса тупого кута паралелограма ділить його сторону на відрізки 5 см і 15 см, починаючи від вершини гострого кута. Обчисліть периметр паралелограма.
14. Перпендикуляр, проведений з вершини прямого кута до однієї з діагоналей прямокутника, поділяє її у відношенні 1 : 3. Доведіть, що одна зі сторін прямокутника дорівнює половині діагоналі.
15.
Дві сторони трикутника дорівнюють 6 см і 4![]() см, а висота, проведена з їхньої спільної вершини, – 4 см. Знайдіть площу трикутника.
см, а висота, проведена з їхньої спільної вершини, – 4 см. Знайдіть площу трикутника.
16. Знайдіть основи трапеції, якщо їх різниця і середня лінія трапеції дорівнюють 10 м.
17. Катети прямокутного трикутника дорівнюють 5 см і 12 см. Знайдіть синуси, косинуси і тангенси кутів трик утника.
18.
Обчисліть кути рівнобічної трапеції, якщо синус одного з них дорівнює 0,5![]() .
.
19. Побудуйте кут, косинус якого дорівнює 0,5. Знайдіть синус і тангенс цього кута.
20. Побудуйте кут, тангенс якого дорівнює 5. Знайдіть синус і косинус цього кута.
21.
Побудуйте рівнобедрений трикутник за бічною стороною 6 cм і кутом при основі, косинус якого дорівнює ![]() .
.
22. Косинуси гострих кутів трапеції дорівнюють 0,8 і 0,6.
Знайдіть синуси, косинуси і тангенси його тупих кутів.
23. Знайдіть невідому сторону АВС , якщо:
а) АВ 3 см, ВС 8 см, В 60;
б) АВ
6![]() см, АС
4 см, А
45.
см, АС
4 см, А
45.
24. Сторони трикутника пропорційні числам 7, 8 і 13. Знайдіть найбільший кут трикутника, якщо його периметр 56 см.
25. Діагоналі паралелограма дорівнюють 12 см і 32 см, а одна зі сторін 14 см. Знайдіть периметр паралелограма і кут між його діагоналями.
26. Діагоналі ромба дорівнюють 16 см і 12 см. Знайдіть периметр і площу ромба.
27. Периметр ромба дорівнює 6,8 см, а одна з діагоналей 1,6 см. Знайдіть площу ромба.
28. Периметр паралелограма дорівнює 52 см, а його площа 60 см2 . Знайдіть сторони і висоти паралелограма, якщо його гострий кут 30.
29.
![]() У рівнобічній трапеції основи дорівнюють 8 см і 18 см. Знайдіть радіус вписаного кола.
У рівнобічній трапеції основи дорівнюють 8 см і 18 см. Знайдіть радіус вписаного кола.
30. Бісектриса прямого кута трикутника ділить гіпотенузу на відрізки 20 дм і 15 дм. Знайдіть площу трикутника.
31. Знайдіть діагоналі рівнобічної трапеції, основи якої дорівнюють 11 см і 21 см, а бічна сторона 13 см.
32. Знайдіть кути опуклого п’ятикутника, якщо вони пропорційні числам 3, 4, 5, 7, 8.
33. Центральний кут правильного п- кутника у 4 рази менший за його внутрішній кут. Знайдіть п .
34. Накресліть коло діаметра 6 см. Впишіть у коло й опишіть навколо нього пра вильні п- кутники та обчисліть їх периметри, якщо: а) п 3; б) п 4; в) п 6; г) п 12.
35. У коло вписано квадрат і правильний шестикутник. Периметр квадрата 24 см. Знайдіть периметр і площу шес тикутника.
36. Навколо кола описано правильний трикутник, а в коло вписано правильний шестикутник, периметр якого 18 см. Знайдіть периметр і площу трикутника.
37. Дано правильний шестикутник зі стороною 4 см. Знайдіть ширину і площу кільця, утвореного колами, вписаним і описаним навколо шестикутника.
38. Знайдіть сторони та площу АВС , якщо A (3; 4), B (–3; 4), C (–3; –4).
39. Дано АВС , у якого А (7; 5), В (4; 1), С (–4; 7). Знайдіть довжини його медіан.
40.
 Відрізок MN
точками K
і Р
поділено на три рівні частини (МK
KР
PN
). Знайдіть координати точки N
, якщо М
(2; –4), Р
(–6; 2).
Відрізок MN
точками K
і Р
поділено на три рівні частини (МK
KР
PN
). Знайдіть координати точки N
, якщо М
(2; –4), Р
(–6; 2).
41. На осі абсцис знайдіть точку М , яка рівновіддалена від початку координат і від точки Р (2; 3).
42. Напишіть рівняння прямої, яка проходить через точки А (1; 4) і В (–2; 1). Знайдіть площу трикутника, який від тинає ця пряма від осей координат.
43. Доведіть, що трикутник з вершинами А (3; 4), В (6; –2), С (–3; 1) – рівнобедрений. Знайдіть його площу.
44. Установіть вид чотирикутника ABCD , якщо A (3; 1), B (4; 6), С (9; 7), D (8; 2). Знайдіть його периметр і площу.
45. Знайдіть координати точки, яка симетрична точці А (3; –5) відносно: а) точки (0; 0); б) осі абсцис; в) осі ординат.
![]()
46. Побудуйте два довільні вектори a і b . Побудуйте вектор d такий, що:
![]() а) d
a
+ b
; б) d
a
– b
;
а) d
a
+ b
; б) d
a
– b
;
в) d a – 3b ; г) d 2a + 0,5b .
47.

Чи рівні вектори AB і CD , якщо A (1; 6), B (3; 2), С (0; –1), D (2; –5)?
![]()
48.
![]() Знайдіть модуль вектора p
2a
– 3b
, якщо a
(1; 3), b
(–2; 0).
Знайдіть модуль вектора p
2a
– 3b
, якщо a
(1; 3), b
(–2; 0).
49. При яких значеннях х вектори a (х ; 2) і b (4; 2x ) колінеарні?
50. При яких значеннях х вектори p (2; х ) і s (х ; х + 3) перпендикулярні?
Б
51. По різні сторони від прямої MN позначено точки А і В так, що МА МВ і NA NB . Доведіть, що АВ MN .
52. У рівнобедреному трикутнику основа дорівнює 30 см. Ви сота, проведена до бічної сторони, поділяє її на відрізки у відношенні 7 : 18, починаючи від вершини. Знайдіть площі
частин трикутника, на які його поділяє ця висота.
53. Сторона трикутника, медіана і висота, проведені до неї, дорівнюють відповідно 34, 25 і 24 см. Знайдіть периметр трикутника.
54. Основи трапеції дорівнюють 6 см і 18 см. У якому відношенні діагоналі діляться точкою перетину?
55. Довжина кола збільшилася на 20 %. На скільки відсотків збільшиться площа вписаного в це коло правильного трикутника?
56. Гіпотенуза прямокутного трикутника дорівнює 12 см, а один з гострих кутів дорівнює 30. Знайдіть радіус кола з центром у вершині цього кута, яке поділяє даний трикутник на дві рівновеликі частини.
57. Батько і дочка стоять одне навпроти одного. Їхні тіні відповідно дорівнюють 3 м і 2,5 м. Який зріст має дочка, якщо зріст батька 183 см?
58. Основи рівнобічної трапеції, в яку можна вписати коло, пропорційні числам 3 і 11. Знайдіть синуси кутів тра- пеції.
59. Знайдіть невідомі сторони АВС , якщо:
а) АВ 5 см, ВС 8 см, В 60;
б) АВ
6 см, АС
4 см, cos B
![]() ;
;
в) АС – АВ 6 см, ВС 8 см, В 120;
г) АС 6 см, ВС 14 см, A 60.
60. Сторони трикутника дорівнюють 11 см, 23 см і 30 см. Знайдіть довжину медіани, бісектриси і висоти, проведених до найбільшої сторони.
61.
![]() У трикутику АВС AB
BC
6 см, sin A
0,4. Знайдіть відстань від точки перетину медіан трикутника до центра кола, описаного навколо трикутника.
У трикутику АВС AB
BC
6 см, sin A
0,4. Знайдіть відстань від точки перетину медіан трикутника до центра кола, описаного навколо трикутника.
62. AL – бісектриса рівнобедреного АВС (АВ ВС ), BL а , A 2. Знайдіть сторони трикутника і довжини його бісектрис.
63. BM – медіана трикутника АВС , BM m , ABM , CBM . Знайдіть АВ .
64. Основи трапеції дорівнюють 6 см і 24 см. Знайдіть радіуси вписаного і описаного кіл.
65. На сторонах АВ і ВС трикутника АВС взято точки K і Т так, що АВ 10 см, АK 2 см, ВС 14 см, ТС 9 см. Знайдіть площу чотирикутника АKTС , якщо SАВС 28 см2 .
66. Основи рівнобічної трапеції ABCD дорівнюють 11 см і 21 см, а бічна сторона – 13 см. Знайдіть радіуси кіл: а) опи саного навколо трапеції; б) вписаного в АВС ; в) впис аного в ACD .
67.
Дано два круги з радіусами по 1 дм, відстань між їх центра ми дорівнює ![]() дм. Знайдіть площу спільної частини цих кругів.
дм. Знайдіть площу спільної частини цих кругів.
68. Спільна хорда двох кругів стягує дуги 60 і 120. Знайдіть відношення радіусів цих кругів.
69. Чотири серпики утворені колом, описаним навколо квадрата, і півколами, побудованими на сторонах квадрата як
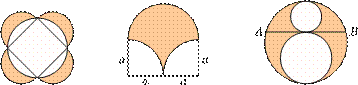
Мал. 33 Мал. 34 Мал. 35
на діаметрах (мал. 33). Доведіть, що сума площ цих чотирьох серпиків дорівнює площі квадрата.
70. Знайдіть площу фігури, заштрихованої на малюнку 34.
71. На малюнку 35 зображено три різні попарно дотичні кола і хорда, яка дотикається до двох менших кіл у їх спільній точці. Знайдіть площу заштрихованої частини більшого круга, якщо до вжина хорди а.
72.
У круговий сектор АОВ
радіуса ОА
10 см вписано коло. Знайдіть відношення площ сектора і круга, якщо SАОВ
25![]() см2
.
см2
.
73. AK , BL , CM – медіани трикутника АВС . Знайдіть координати точки L , якщо А (–3; –1), В (–2; 1), K (1; –1).
74. Знайдіть сторони та площу трикутника АВС , якщо A (a ; b ), B (–a ; b ), C (–a ; –b ) і точка А лежить у III координатній чверті.
75. Дано трикутник АВС , у якого А (7; 5), В (4; 1), С (–4; 7). Знайдіть довжини медіани, висоти і бісектриси, проведених з вершини В .
76.
![]()
Використовуючи умову попередньої задачі, напишіть рівняння медіани, висоти і бісектриси, проведених з верш и ни В .
77. Точки А (2; –5) і С (2; –1) є вершинами квадрата ABCD . Напишіть рівняння кола, вписаного в цей квадрат, та кола, опи- саного навколо нього. Знайдіть невідомі вершини квадрата.
78. Запишіть рівняння прямої, яка проходить через центри двох кіл: х 2 + у 2 – 4х + 2у 0 і х 2 + у 2 + 4х – 6у 3.
79. Чи має трикутник АВС , у якого А (–6; –1), В (–3; 5), С (3; 2), вісь симетрії? Якщо має, то запишіть її рівняння.
80. АС – діагональ квадрата. Запишіть рівняння осей симетрії цього квадрата, якщо А (1; 2), С (5; 6).
81. Коло радіуса 3 дотикається до осей координат у І чверті. Запишіть рівняння цього кола і кола, симетричного даному відносно: а) початку координат; б) осі абсцис; в) осі ординат; г) прямої у 2х.
82.
О
– точка перетину медіан рівностороннього трикутника АВС
. При паралельному перенесенні точка А
відобразилася на точку О
. Виконайте паралельне перенесення АВС
. Знай діть периметр побудованого трикутника, якщо SАОВ
S
![]() .
.
83. При гомотетії відносно початку координат точка А (1; 2) переходить у точку А 1 (3; 6). У яку точку при цій гомотетії перейде точка В (3; –2)? Знайдіть коефіцієнт гомотетії.
84. Ромби ABCD і MNPK – подібні, АС : BD 4 : 5. Знайдіть діагоналі ромба MNPK , якщо його площа дорівнює 40 см2 .
85. Пряма MN , паралельна основі АС трикутника АВС , ділить його на дві частини – трикутник і трапецію. Площі цих фігур пропорційні числам 1 і 3. Знайдіть периметр АВС , якщо периметр MBN дорівнює 7 см .
86.
 П
обудуйте три довільні вектори a
, b
, c
. Побудуйте вектор d
такий, що:
П
обудуйте три довільні вектори a
, b
, c
. Побудуйте вектор d
такий, що:
а) d a + 2b ; б) d 2a – 3b ;
в) d 0,5a – 3b + 2c ; г) d a + 0,5b – 2c .
![]()
87.
 Знайдіть модуль вектора m
a
+ 2b
, якщо |a
| 2, |b
| 1,
Знайдіть модуль вектора m
a
+ 2b
, якщо |a
| 2, |b
| 1,
.
88. Знайдіть косинус кута А трикутника АВС , якщо A (–1; 2), B (3; 5), С (2; –1).
89.
![]() П
ри яких значеннях а
кут між вект орами m
(6; а
) і b
(–5; а
– 1) тупий?
П
ри яких значеннях а
кут між вект орами m
(6; а
) і b
(–5; а
– 1) тупий?
90. Знайдіть кут між одиничними векторами a і b , якщо век-
![]()
тор 5a – 4b пер пен ди кулярний до вектора a – 2b .
91.
![]() Дано точки А
(4; –2) і B
(2; –5). Запишіть рівняння прямої, яка дотикається до кола діаметра АВ
у точці А
.
Дано точки А
(4; –2) і B
(2; –5). Запишіть рівняння прямої, яка дотикається до кола діаметра АВ
у точці А
.
92. Запишіть рівняння дотичних, проведених з точки A (5; 0) до кола х 2 + у 2 9.
93. На діаграмі Вороного зображено три антени A , В , C , їх коорд инати та області обслуговування (мал. 36). Ребра OM , ON , OK клітин на діаграмі Вороного будуються як серединні перпендикуляри до відрізків АВ , ВС і АС . Запишіть рівняння ребер діаграми Вороного і координати точки О – вершини діаграми Вороного.

Георгій Феодосійович
Мал. 36 ВОРОНИЙ (1868–1908)
94*. На сторонах АВ , ВС і СА три кутни ка АВС позначено точки А 1 , В 1 , С 1 такі, що АС 1 : С 1 В ВА 1 : А 1 С СВ 1 : В 1 А 2 (мал. 37). Як відносяться площі трикутників АВС і KРТ ?
95*. На сторонах довільного трикутника АВС зовні нього побудовано правильні трикутники (мал. 38). Доведіть, що їх центри K , Р , Т – вершини прав иль них трикутників.
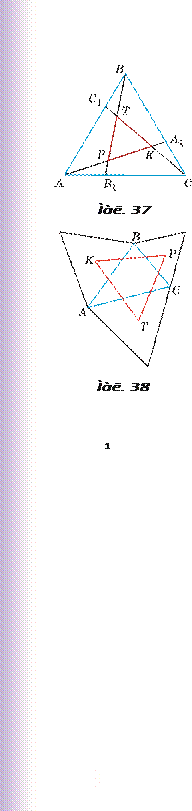 96.
На основі АС
трикутника АВС
взято точки М
і Н
такі, що АМ
< AH
. Прямі ВМ
і ВH
ділять медіану АK
на три рів ні частини. Знайдіть АС
, якщо МН
3. 97*.
Протилежні сторони опуклого шестикутника паралельні. Доведіть, що прямі, які сполучають середини протилежних сторін, перетинаються в одній точці.
96.
На основі АС
трикутника АВС
взято точки М
і Н
такі, що АМ
< AH
. Прямі ВМ
і ВH
ділять медіану АK
на три рів ні частини. Знайдіть АС
, якщо МН
3. 97*.
Протилежні сторони опуклого шестикутника паралельні. Доведіть, що прямі, які сполучають середини протилежних сторін, перетинаються в одній точці.
98*. Пряма Ейлера проходить через центр вписаного у трикутник кола. Дове діть, що трикутник рівнобедрений.
99*. Якщо вписане в трикутник коло дотикається до його сторін АВ , ВС , СА в точках А 1 , В 1 , С 1 , то прямі АА 1 , ВВ 1 , СС перетинаються в одній точці. Доведіть.
100*. На катетах АС і ВС прямокутного трикутника АВС зовні нього побудовано квадрати АСKР і СВМТ . Доведіть, що прямі АМ , ВР і висота СН трикутника перетинаються в одній точці.
[1] . З найдіть координати вектора m 2p + 3q , якщо p (–2; 1), q (4; –3).
а) (8; –7); б) (–14; 0); в) (8; 11); г) (–2; 3).